Solución de inecuaciones de segundo grado por el método de separación de punto. Cálculo diferencial.

Introducción.

Este tema muestra algunos ejemplos de como resolver inecuaciones de segundo grado; se toma en cuenta que la variable «x» representa la incógnita. Se debe tomar en cuenta las propiedades de las inecuaciones.

Problemas resueltos.

Problema 1. Resolver la siguiente inecuación:

${x}^{2} \ge 9$

Solución. De la siguiente inecuación

${x}^{2} \ge 9$

El miembro izquierdo se quedan todos los términos y el miembro del lado derecho quedará cero, además, de respetar el símbolo de la desigualdad:

${x}^{2}-9 \ge 0$

Luego, se factoriza el término cuadrático:

$(x+3)(x-3) \ge 0$

Del primer término

$x+3 \ge 0 \quad \quad \quad x-3 \ge 0$

Del segundo término

$x \ge -3 \quad \quad \quad x \ge 3$

Estos dos resultados representan el intervalo en donde el símbolo “mayor o igual que” representa la existencia de, para el primer término, valores mayores o iguales que “-3” y, para el segundo término, valores mayores o iguales que “3”. Por lo que sus intervalos son tres, entonces:

$(-\infty,-3) \quad \quad (-3,3) \quad \quad (3,\infty)$

El siguiente paso es llevar a cabo los puntos de prueba en cada intervalo.

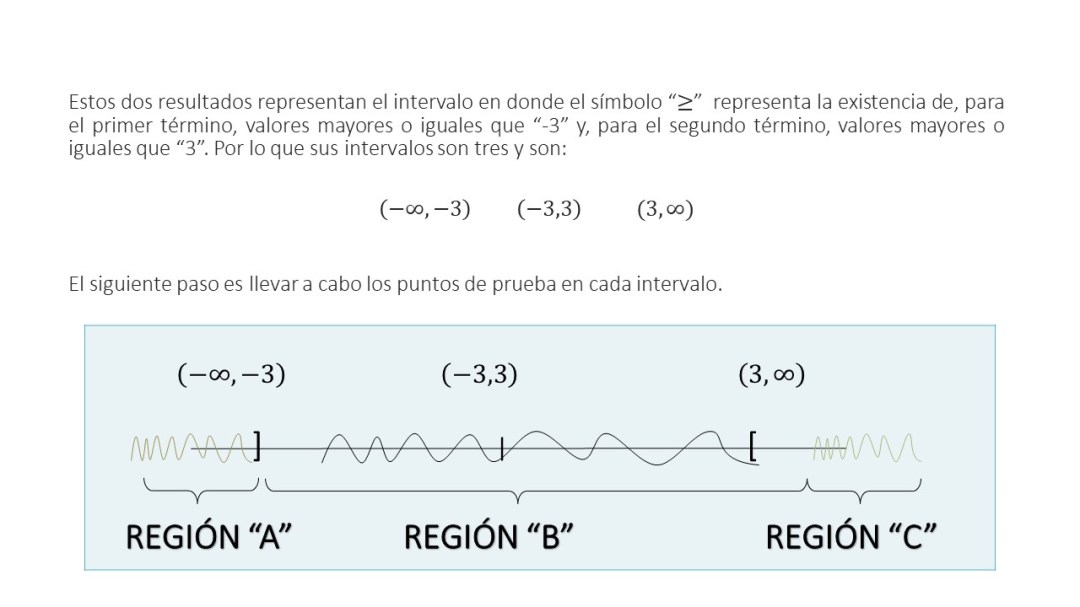
Diapositiva3 — *Figura 1.4.1. Representando las regiones de cada intervalo obtenido de la solución del problema 1.*

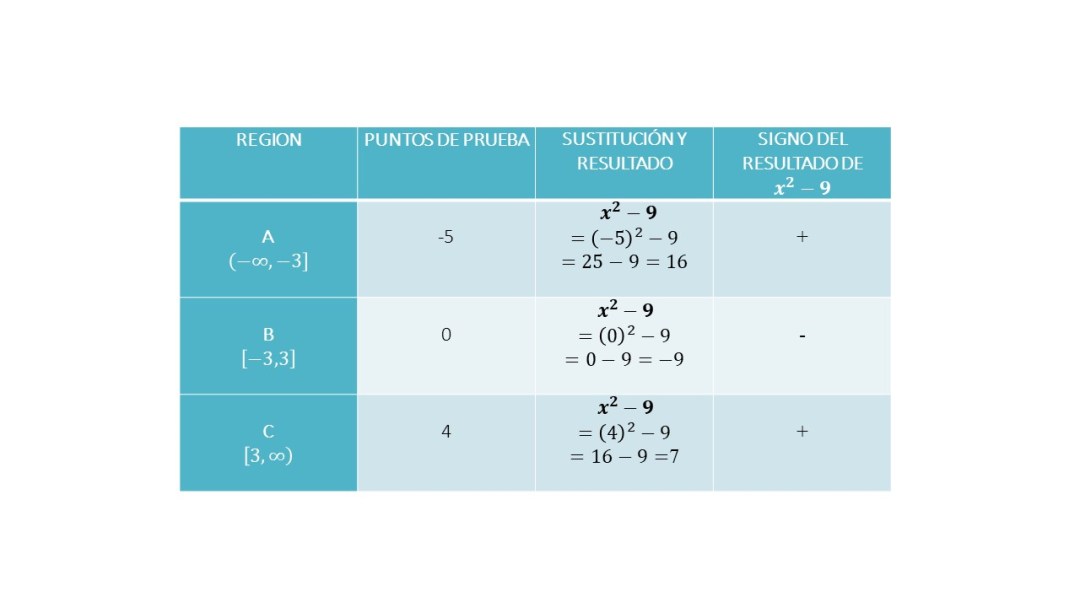
Diapositiva4 — *Figura 1.4.2. Realizando los puntos de prueba en cada intervalo.*

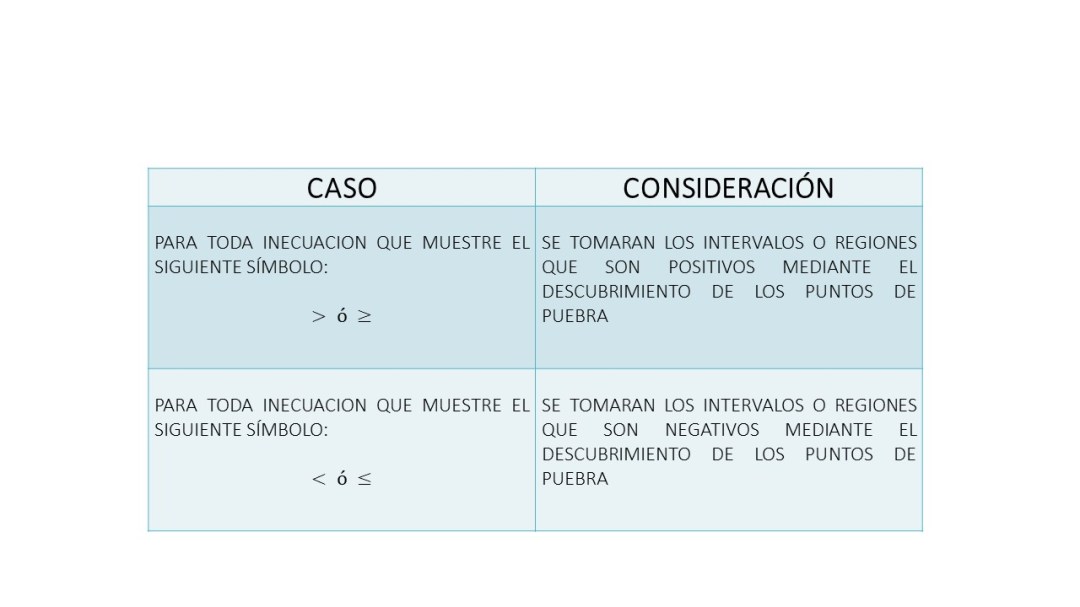
Diapositiva5 — *Figura 1.4.3. Analizando los intervalos y tomando consideraciones.*

La inecuación tiene un símbolo que está hacia la derecha, por lo que en la representación gráfica solo se toman las regiones A y C. Por lo tanto, la notación intervalo es:

$A \cup C$

$(-\infty,-3] \cup [3,\infty)$

Recordando que la región A unifica a la región C. Y la notación conjunto es:

$\left\{x|x6 \right\}$

Problema 2. Resolver la siguiente inecuación:

${x}^{2}<20$

Solución. De la siguiente inecuación:

${x}^{2}<20$

El miembro izquierdo se quedan todos los términos y el miembro del lado derecho quedará cero, además, de respetar el símbolo de la desigualdad:

${x}^{2}-x-20<0$

Factorizando la ecuación de segundo grado:

$(x-5)(x+4)<0$

Del primer término

$x-5<0 \quad \quad \quad x+4<0$

Del segundo término

$x<5 \quad \quad \quad x<-4$

Estos dos resultados representan el intervalo en donde el símbolo “menor que” representa la existencia, para el primer término, valores menores que “5” y, del segundo término, valores menores que “-4”. Por lo que sus intervalos son tres y son:

$(-\infty,-4) \quad \quad (-4,5) \quad \quad (5,infty)$

El siguiente paso es llevar a cabo los puntos de prueba en cada intervalo.

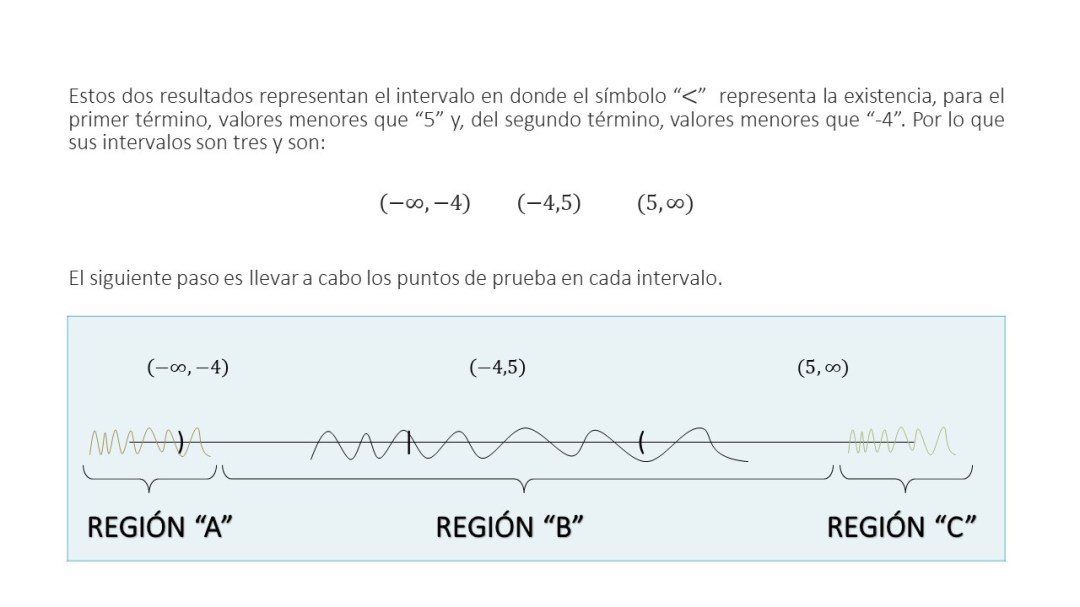
Diapositiva8 — *Figura 1.4.4. Representando las regiones de cada intervalo obtenido de la solución del problema 2.*

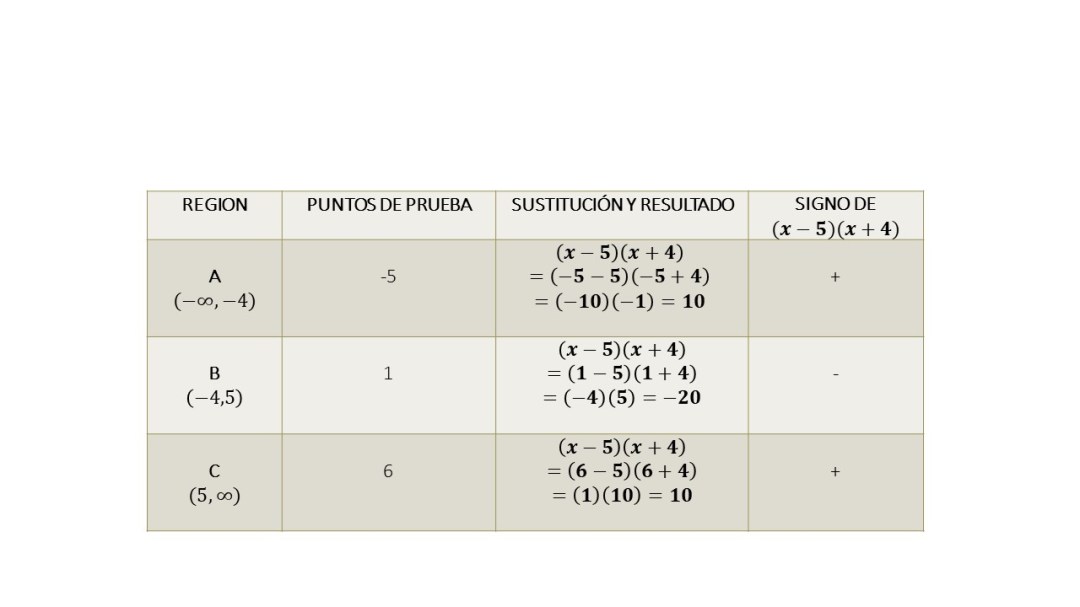
Diapositiva9 — *Figura 1.4.5. Realizando los puntos de prueba en cada intervalo.*

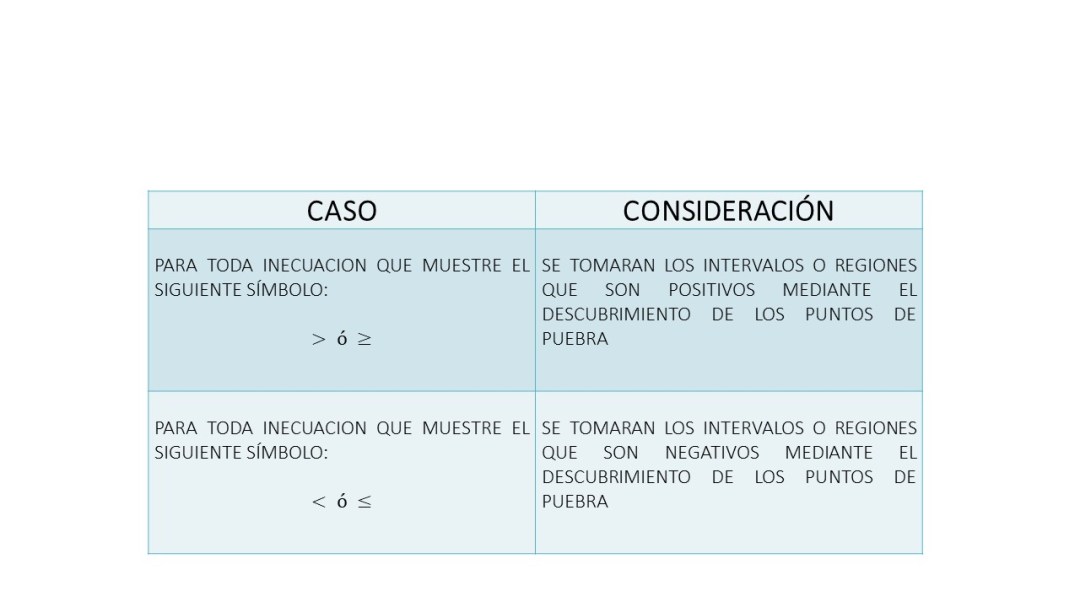
Diapositiva10 — *Figura 1.4.6. Analizando el comportamiento de los puntos de prueba y tomando consideraciones.*

La inecuación tiene un símbolo que está hacia la izquierda, por lo que en la representación gráfica solo se toma la región B. Por lo tanto, la notación intervalo es:

$B=(-4, 5)$

Recordando que B es la región B. Y la notación conjunto es:

$\left\{x|-4 <x<5 \right\}$

Referencias bibliográficas.

Aguilar Márquez, A., Bravo Vázquez, F. V., Gallegos Ruiz, H. A., Cerón Villegas, M., & Reyes Figueroa, R. (2009). Matemáticas simplificadas. México: Pearson Educación.
Gil Sevilla, J. L., & Díaz Téllez, R. (2013). Cálculo diferencial para cursos enfoque por competencias. México: Pearson Educación.
Mitacc, M., & Toro Mota, L. (2009). Tópicos de cálculo. Volumen 1. Perú: Thales S. R. L.
Swokowski, E. W. (1989). Cálculo con geometría analítica. México: Panamericana.
Thomas, J. G. (2006). Cálculo. Una variable. México: Pearson Educación.
Zill, D. G. (1999). Cálculo con geometría analítica. México.
Zill, D. G., & Wright, W. S. (2010). Matemáticas 1. Cálculo diferencial. México: Mc Graw Hill Interamericana.

Solución de inecuaciones de segundo grado por el método de separación de punto. Cálculo diferencial.

Introducción.

Problemas resueltos.

Referencias bibliográficas.

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta

Solución de inecuaciones de segundo grado por el método de separación de punto. Cálculo diferencial.

Introducción.

Problemas resueltos.

Referencias bibliográficas.

Comparte esto:

Relacionado

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta