Pendientes y rectas tangentes. Cálculo vectorial.

Pendiente en forma polar

Si $f$ es una función diferenciable (o derivable) de θ, entonces la pendiente de la recta tangente a la gráfica de $r=f(\theta)$ en el punto (r, θ) es

$\displaystyle \frac{dy}{dx} = \frac{\frac{dy}{d\theta}}{\frac{dx}{d\theta}} = \frac{f(\theta) \cos{\theta} + {f}^{'} (\theta) \sin{\theta}}{-f(\theta) \sin{\theta} + {f}^{'} (\theta) \cos{\theta}}$

siempre que $\displaystyle \frac{dx}{d\theta} \ne 0$ en (r, θ).

De acuerdo a lo anterior, se tienen las siguientes consideraciones:

Las soluciones $\displaystyle \frac{dy}{d\theta} = 0$ brinda una tangente horizontal, siempre que $\displaystyle \frac{dx}{d\theta} \ne 0$ .
Las soluciones $\displaystyle \frac{dx}{d\theta} = 0$ brinda una tangente vertical, siempre que $\displaystyle \frac{dy}{d\theta} \ne 0$ .
Si $\displaystyle \frac{dy}{d\theta} = 0$ y $\displaystyle \frac{dx}{d\theta} = 0$ son simultáneamente no se puede concluir respecto a las rectas tangentes.

*Figura 1. Representando recta tangente en una curva polar.*

Rectas tangentes en el polo

Si f(α)=0 y f'(α) $\ne$ 0, entonces la recta $\theta = \alpha$ es tangente a la gráfica de $r = f(\alpha)$ en el polo.

Problema resueltos

Problema 1. Hallar las rectas tangentes horizontales y verticales de la siguiente ecuación e intervalo: $r=\sin{\theta}$ , $0 \le \theta \le \pi$ .

Solución. Utilizando la ecuación del problema y sustituyéndolo con la ecuación siguiente

$x = r \cos{\theta}$

$x = (\sin{\theta})(\cos{\theta})$

$x = \sin{\theta} \cos{\theta}$

Derivando esta ecuación con respecto a θ

$\displaystyle \frac{dx}{d\theta} = \frac{d}{d\theta} (\sin{\theta} \cos{\theta})$

$\displaystyle \frac{dx}{d\theta} = (\sin{\theta})(-\sin{\theta}) + (\cos{\theta})(\cos{\theta})$

$\displaystyle \frac{dx}{d\theta} = -{\sin}^{2}{\theta} + {\cos}^{2}{\theta}$

$\displaystyle \frac{dx}{d\theta} = {\cos}^{2}{\theta} - {\sin}^{2}{\theta}$

Ahora, si dx/dθ = 0, se despeja el parámetro θ

$\displaystyle \frac{dx}{d\theta} = {\cos}^{2}{\theta} - {\sin}^{2}{\theta}$

$0 = {\cos}^{2}{\theta} - {\sin}^{2}{\theta}$

$0 = {\cos}^{2}{\theta} - (1 - {\cos}^{2}{\theta})$

$0 = 2 {\cos}^{2}{\theta} - 1$

$2 {\cos}^{2}{\theta} - 1 = 0$

$2 {\cos}^{2}{\theta} = 1$

$\displaystyle {\cos}{\theta} = \frac{1}{\sqrt{2}}$

$\displaystyle \theta = \arccos{\left(\frac{1}{\sqrt{2}} \right)}$

$\displaystyle \theta = \frac{1}{4} \pi$ y $\displaystyle \theta = \frac{3}{4} \pi$

Cuando $\displaystyle \theta = \frac{1}{4} \pi = 45$ °, se sustituye en la ecuación del problema

$r = \sin{\theta}$

$\displaystyle r = \sin{\frac{\pi}{4}}$

$\displaystyle r = \frac{1}{\sqrt{2}}$

Cuando $\displaystyle \theta = \frac{3}{4} \pi = 135$ °, se sustituye en la ecuación del problema

$r =\sin{\theta}$

$\displaystyle r = \sin{\frac{3}{4} \pi}$

$\displaystyle r = \frac{1}{\sqrt{2}}$

Por lo tanto, los puntos verticales son $\displaystyle \left(\frac{1}{2} , \frac{1}{4} \pi \right)$ y $\displaystyle \left(\frac{1}{2}, \frac{3}{4} \pi \right)$

Ahora, tomando nuevamente la ecuación del problema y sustituyéndolo con la ecuación siguiente

$y = r \sin{\theta}$

$y = (\sin{\theta})(\sin{\theta})$

$y = {\sin}^{2}{\theta}$

Derivándolo con respecto a θ

$\displaystyle \frac{dy}{d\theta} = \frac{d}{d\theta} ({\sin}^{2}{\theta})$

$\displaystyle \frac{dy}{d\theta} = 2 \sin{\theta} \cos{\theta}$

Ahora, haciendo que dy/dθ = 0, se despeja el parámetro θ

$\displaystyle \frac{dy}{d\theta} = 2 \sin{\theta} \cos{\theta}$

$0 = 2 \sin{\theta} \cos{\theta}$

$0 = \sin{2 \theta}$

$\arcsin{(0)} = 2\theta$

$2\theta = \arcsin{(0)}$

Y se obtienen dos soluciones

$2\theta = 0$ y $2\theta = \pi$

Al despejar θ en ambas

$\theta = 0$ y $\displaystyle \theta = \frac{\pi}{2}$

Cuando θ=0, el valor de $r$ es

$r = \sin{\theta}$

$r = \sin{0}$

$r = 0$

Cuando $\displaystyle \theta = \frac{1}{2} \pi$ , el valor de $r$ es

$\displaystyle r = \sin{\theta}$

$\displaystyle r = \sin{(\frac{1}{2}\pi)}$

$r = 1$

Por lo tanto, los puntos horizontales son $(0, 0)$ y $\displaystyle (1, \frac{\pi}{2})$ .

*Figura 2. Ubicación de las rectas tangentes verticales y horizontales de la curva r=sen θ*.

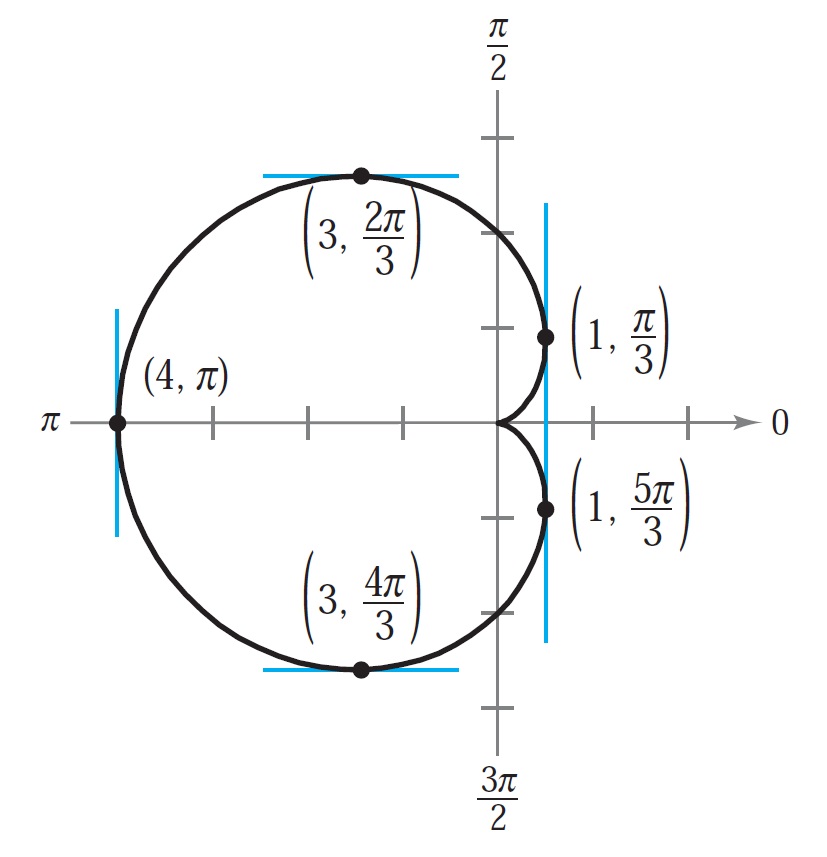
Problema 2. Hallar las rectas tangentes horizontales y verticales de la siguiente ecuación $r = 2(1 - \cos{\theta})$ .

Solución. Utilizando $x=r \cos{\theta}$ y sustituyéndolo en la ecuación del problema

$x = r \cos{\theta}$

$x = 2(1 - \cos{\theta})(\cos{\theta})$

$x = 2(\cos{\theta} - {\cos}^{2}{\theta})$

Derivándolo con respecto a θ

$\displaystyle \frac{dx}{d\theta} = \frac{d}{d\theta} [2(\cos{\theta} - {\cos}^{2}{\theta})]$

$\displaystyle \frac{dx}{d\theta} = 2[-\sin{\theta} - 2 \cos{\theta}(-\sin{\theta})]$

$\displaystyle \frac{dx}{d\theta} = 2(-\sin{\theta} + 2 \sin{\theta} \cos{\theta})$

$\displaystyle \frac{dx}{d\theta} = - 2 \sin{\theta} + 4 \sin{\theta} \cos{\theta}$

Ahora, haciendo que dx/dθ=0, se despeja el parámetro θ

$\displaystyle \frac{dx}{d\theta} = -2 \sin{\theta} + 4 \sin{\theta} \cos{\theta}$

$0 = -2 \sin{\theta} + 4 \sin{\theta} \cos{\theta}$

$-2 \sin{\theta} + 4 \sin{\theta} \cos{\theta} = 0$

$- \sin{\theta} + 2 \sin{\theta} \cos{\theta} = 0$

$\sin{\theta}(-1 + 2 \cos{\theta}) = 0$

Eligiendo el primer término $\sin{\theta}$ , se tiene lo siguiente:

$\sin{\theta}= 0$

$\theta= \arcsin{(0)}$

Como existen dos valores de θ

$\theta= 0$ y $\theta = \pi$

Cuando $\theta = 0$ ,

$r = 2(1 - \cos{\theta})$

$r = 2(1 - \cos{0}) = 2(1 - 1)$

$r = 0$

Cuando $\theta = \pi$ ,

$r = 2(1 - \cos{\theta})$

$r = 2(1 - \cos{\pi}) = 2[1 - (- 1)]$

$r = 4$

Los primeros puntos verticales son $(0,0)$ y $(4,\pi)$ . Eligiendo el segundo término $-1 + 2 \cos{\theta}$ , se tiene lo siguiente:

$-1 + 2 \cos{\theta} = 0$

$\displaystyle \cos{\theta} = \frac{1}{2}$

$\displaystyle \theta = \arccos{(\frac{1}{2})}$

Por lo que existen dos valores de θ y son

$\displaystyle \theta = \frac{1}{3}\pi$ y $\displaystyle \theta = \frac{5}{3} \pi$

Cuando $\displaystyle \theta =\frac{ \pi}{3}$ , se sustituye en la ecuación del problema

$r = 2(1 - \cos{\theta})$

$\displaystyle r = 2(1 - \cos{\frac{1}{3} \pi})$

$\displaystyle r = 2(1 - \frac{1}{2}) = 1$

$r = 1$

Cuando $\displaystyle \theta = \frac{5}{3}\pi$ , se tiene que

$r = 2(1 - \cos{\theta})$

$\displaystyle r = 2(1 - \cos{\frac{5}{3}\pi)}$

$\displaystyle r = 2(1 - \frac{1}{2}) = 1$

$r = 1$

Por lo tanto, los puntos verticales son $\displaystyle (1, \frac{1}{3} \pi)$ y $\displaystyle (1, \frac{5}{3}\pi)$ . Utilizando $y=r \sin{\theta}$ y sustituyéndolo en la ecuación del problema

$y = r \sin{\theta}$

$y = 2(1 - \cos{\theta})(\sin{\theta})$

$y = 2(\sin{\theta} - \sin{\theta} \cos{\theta})$

$y = 2 \sin{\theta} - 2 \sin{\theta} \cos{\theta}$

Derivándolo con respecto a θ

$\displaystyle \frac{dy}{d\theta} = \frac{d}{d\theta} (2 \sin{\theta} - 2 \sin{\theta} \cos{\theta})$

$\displaystyle \frac{dy}{d\theta} = 2 \cos{\theta} - 2 \sin{\theta} (- \sin{\theta}) - 2(\cos{\theta})(\cos{\theta})$

$\displaystyle \frac{dy}{d\theta} = 2 \cos{\theta} + 2 {\sin}^{2}{\theta} - 2 {\cos}^{2}{\theta}$

Ahora, haciendo que dy/dθ=0, se despeja el parámetro θ

$\displaystyle \frac{dy}{d\theta} = 2 \cos{\theta} + 2 {\sin}^{2}{\theta} - 2 {\cos}^{2}{\theta}$

$0 = 2 \cos{\theta} + 2 {\sin}^{2}{\theta} - 2{\cos}^{2}{\theta}$

$2 \cos{\theta} + 2 {\sin}^{2}{\theta} - 2 {\cos}^{2}{\theta} = 0$

$2(\cos{\theta} + {\sin}^{2}{\theta} - {\cos}^{2}{\theta}) = 0$

$\displaystyle \cos{\theta} + {\sin}^{2}{\theta} - {\cos}^{2}{\theta} = \frac{0}{2}$

$\cos{\theta} + {\sin}^{2}{\theta} - {\cos}^{2}{\theta} = 0$

Recordando la identidad trigonométrica

${\sin}^{2}{\theta} = 1 - {\cos}^{2}{\theta}$

Entonces, sustituyendo lo anterior

$\cos{\theta} + {\sin}^{2}{\theta} - {\cos}^{2}{\theta} = 0$

$\cos{\theta} + 1 - {\cos}^{2}{\theta} - {\cos}^{2}{\theta} = 0$

$-2 {\cos}^{2}{\theta} + \cos{\theta} + 1 = 0$

Para resolverlo, se usa fórmula general donde los coeficientes de esta ecuación son: a=-2, b=1, c=1.

$\displaystyle \cos{\theta} = \frac{-(1) \pm \sqrt{{(1)}^{2} - 4(-2)(1)}}{2(-2)}$

$\displaystyle \cos{\theta} = \frac{-1 \pm \sqrt{1+8}}{-4}$

$\displaystyle \cos{\theta} = \frac{-1 \pm \sqrt{9}}{-4} = \frac{-1 \pm 3}{-4}$

Tomando la parte positiva

$\displaystyle \cos{{\theta}_{1}} = \frac{-1 + 3}{-4} = \frac{2}{-4} = -\frac{1}{2}$

$\displaystyle {\theta}_{1} = \arccos{(-\frac{1}{2})}$

$\displaystyle {\theta}_{1} = \frac{2}{3}\pi$ y $\displaystyle{\theta}_{1} = \frac{4}{3}\pi$

Cuando $\displaystyle \theta = \frac{2}{3}\pi$ y sustituyéndolo en la ecuación del problema

$r = 2(1 - \cos{\theta})$

$\displaystyle r = 2(1 - \cos{\frac{2}{3}\pi})$

$\displaystyle r = 2(1 + \frac{1}{2})$

$\displaystyle r = 2(\frac{3}{2})$

$r = 3$

Cuando $\displaystyle \theta = \frac{4}{3} \pi$ y sustituyéndolo en la ecuación del problema

$r = 2(1 - \cos{\theta})$

$\displaystyle r = 2(1 - \cos{\frac{4}{3}\pi})$

$\displaystyle r = 2(1 + \frac{1}{2})$

$r = 2(\frac{3}{2})$

$r = 3$

Luego, tomando la parte negativa

$\displaystyle \cos{{\theta}_{2}} = \frac{-1-3}{-4} = \frac{-4}{-4} = 1$

${\theta}_{2} = \arccos{(1)}$

${\theta}_{2} = 0$ y ${\theta}_{2} = 2\pi$

Cuando θ=0 y sustituyéndolo en la ecuación del problema

$r = 2(1 - \cos{\theta})$

$r = 2(1 - \cos{0}) = 2(1 - 1) = 2(0)$

$r = 0$

Cuando θ=2π y sustituyéndolo en la ecuación del problema

$r=2(1 - \cos{\theta})$

$r = 2(1 - \cos{2\pi}) = 2(1 - 1) = 2(0)$

$r = 0$

Por lo tanto, los puntos horizontales son $(0,0)$ , $\displaystyle \left(3, \frac{2}{3}\pi \right)$ y $\displaystyle \left(3, \frac{4}{3}\pi \right)$

*Figura 3. Ubicación de las rectas tangentes verticales y horizontales de la curva r=2(1-cos θ)*.

Problema 3. Encontrar las rectas tangentes en el polo para la curva rosa de 3 pétalos, $f(\theta) = 2 \cos{3\theta}$ .

Solución. Primero se determina en que momento la función es cero. Para ello, se iguala a cero

$\displaystyle f(\theta) = 2 \cos{3 \theta}$

$\displaystyle 2 \cos{3 \theta} = 0$

$\displaystyle \cos{3 \theta} = 0$

$\displaystyle 3 \theta = \arccos{(0)}$

Existen tres valores, $\displaystyle \theta = \frac{\pi}{2}$ , $\displaystyle \theta = \frac{3\pi}{2}$ y $\displaystyle \theta = \frac{5\pi}{2}$ . Cuando $\displaystyle \theta = \frac{\pi}{2}$ ,

$\displaystyle 3 \theta = \frac{\pi}{2}$

$\displaystyle \theta = \frac{\pi}{6}$

Cuando $\displaystyle \theta = \frac{3\pi}{2}$ ,

$\displaystyle 3 \theta = \frac{3\pi}{2}$

$\displaystyle \theta = \frac{\pi}{2}$

Cuando $\displaystyle \theta = \frac{5\pi}{2}$ ,

$\displaystyle 3 \theta = \frac{5\pi}{2}$

$\displaystyle \theta = \frac{5\pi}{6}$

Una manera de comprobar que estos resultados sean correctos es, primero derivando la función y después demostrar que al evaluarlos en la curva no den resultados nulos (de acuerdo con el teorema).

\displaystyle \theta = \frac{\pi}{6} = \alpha

\displaystyle \theta = \frac{\pi}{2} = \alpha

Como los valores son diferentes de cero, se concluye que las rectas tangentes en el polo son: $\displaystyle \theta = \frac{\pi}{6}$ , $\displaystyle \theta = \frac{\pi}{2}$ y $\displaystyle \theta = \frac{5\pi}{6}$

Cuando $\displaystyle \theta = \frac{\pi}{6} = \alpha$	Cuando $\displaystyle \theta = \frac{\pi}{2} = \alpha$	Cuando $\displaystyle \theta = \frac{5\pi}{6} = \alpha$
$\displaystyle f(\theta) = 2 \cos{3 \theta}$ $\displaystyle f'(\theta) = -6 \sin{3 \theta}$ $\displaystyle f'(\theta) = -6 \sin{3 \left(\frac{\pi}{6} \right)}$ $\displaystyle f'(\theta) = -6 \sin{\frac{\pi}{2}} = -6 (1)$ $\displaystyle f'(\theta) = -6$	$\displaystyle f(\theta) = 2 \cos{3 \theta}$ $\displaystyle f'(\theta) = -6 \sin{3 \theta}$ $\displaystyle f'(\theta) = -6 \sin{3 \left(\frac{\pi}{2} \right)}$ $\displaystyle f'(\theta) = -6 \sin{\frac{3\pi}{2}} = -6 (-1)$ $\displaystyle f'(\theta) = 6$	$\displaystyle f(\theta) = 2 \cos{3 \theta}$ $\displaystyle f'(\theta) = -6 \sin{3 \theta}$ $\displaystyle f'(\theta) = -6 \sin{3 \left(\frac{5\pi}{6} \right)}$ $\displaystyle f'(\theta) = -6 \sin{\frac{5\pi}{2}} = -6 (1)$ $\displaystyle f'(\theta) = -6$

Pendientes y rectas tangentes. Cálculo vectorial.

Pendiente en forma polar

Rectas tangentes en el polo

Problema resueltos

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta

Pendientes y rectas tangentes. Cálculo vectorial.

Pendiente en forma polar

Rectas tangentes en el polo

Problema resueltos

Comparte esto:

Relacionado

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta