Introducción

Para cambiar una integral doble de coordenadas rectangulares a coordenadas polares se hace una transformación. Iniciando (desde el centro de la doble integral hacia afuera), los límites inferior y superior de la primera integral representan el radio de la circunferencia y, después, los límites de la segunda integral representan el área bajo la curva. Y finalmente, la conversión es la siguiente:

\displaystyle \int_{c}^{d}{\int_{a}^{b}{f(x, y) dy} dx} = \int_{\theta_1}^{\theta_2}{\int_{r_1}^{r_2}{f(r\sin{\theta}, r \cos{\theta})r dr} d\theta}

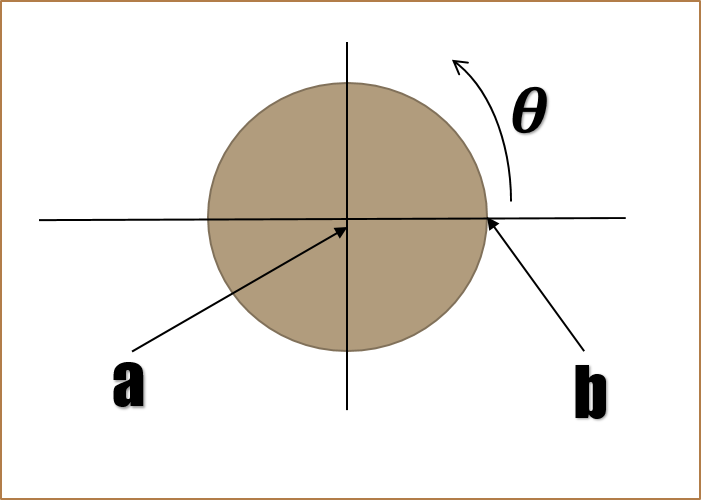
Imagen1
Figura 1. Representación gráfica de la interpretación geométrica de la integral definida en coordenadas polares. 

Algunos datos a tomar en cuenta

Coordenadas rectangularesCoordenadas polares
x^2+y^2=r^2x = r \cos{\theta}
\displaystyle x = \sqrt{r^2-y^2}y = r \sin{\theta}
\displaystyle y = \sqrt{r^2-x^2}\displaystyle \arctan{\theta} = \frac{y}{x}

Conversión de radianes a grados y viceversa

De radianes a gradosDe grados a radianes
\displaystyle grados = radianes \cdot (\frac{180}{\pi})\displaystyle radianes = grados \cdot (\frac{\pi}{180})

Problemas resueltos

Problema 1. Resolver la siguiente integral

\displaystyle \int_{0}^{2\pi}{\int_{0}^{6}{3r^2 \sin{\theta} \ dr}d\theta}

Solución. La primera integral (tomando de adentro hacia afuera) la diferencial dr presenta variables de r

\displaystyle \int_{0}^{2\pi}{\int_{0}^{6}{3r^2 \sin{\theta} dr}d\theta}

Resolviendo la integral

\displaystyle \int_{0}^{6}{(\sin{\theta})3r^2 dr} = 3 \sin{\theta}\int_{0}^{6}{r^2 dr} = 3 \sin{\theta} \left[ \frac{1}{3} r^3 \right]_{0}^{6}

\displaystyle = 3 \sin{\theta} [\frac{1}{3} {(6)}^{3} - \frac{1}{3} {(0)}^{3}] = 3 \sin{\theta} (36) = 216 \sin{\theta}

Después

\displaystyle \int_{0}^{2\pi}{\int_{0}^{6}{3r^2 \sin{\theta} dr}d\theta} = \int_{0}^{2\pi}{216 \sin{\theta}d\theta}

\displaystyle = 216\int_{0}^{2\pi}{\sin{\theta}d\theta} = \left[ 216(-\cos{\theta}) \right]_{0}^{2\pi} = \left[216(-\cos{\theta}) \right]_{0}^{\pi}

\displaystyle = 216(-\cos{2\pi} + \cos{0}) = 216(-1+1) = 0

Por lo tanto

\displaystyle \therefore \int_{0}^{2\pi}{\int_{0}^{6}{3r^2 \sin{\theta} \ dr}d\theta} = 0

Problema 2. Resolver la siguiente integral

\displaystyle \int_{0}^{\frac{\pi}{2}}{\int_{2}^{3}{\sqrt{9-r^2} rdr}d\theta}

Solución. La primera integral (tomando de adentro hacia afuera) la diferencial dr presenta variables de r

\displaystyle \int_{0}^{\frac{\pi}{2}}{\int_{2}^{3}{\sqrt{9-r^2} rdr}d\theta}

Entonces, dentro de la integral, se resuelve aplicando el método de sustitución

\displaystyle \int_{2}^{3}{\sqrt{9-r^2} r dr} \Rightarrow \int{\sqrt{9-r^2} r dr}

Donde

h = 9 - r^2\displaystyle \frac{dh}{dr} = -2r\displaystyle \frac{dh}{(-2)} = r dr

Sustituyendo

\displaystyle \int{\sqrt{9-r^2} r dr} = \int{\sqrt{h} \frac{dh}{(-2)}} = -\frac{1}{2} \int{\sqrt{h} dh}

\displaystyle = -\frac{1}{2} \int{\sqrt{h} dh} = -\frac{1}{2} \int{{h}^{\frac{1}{2}} dh} = -\frac{1}{2} \int{{h}^{\frac{1}{2}} dh}

\displaystyle = -\frac{1}{2} [\frac{{h}^{\frac{3}{2}}}{\frac{3}{2}} + C] = -\frac{1}{2}[\frac{2}{3} {h}^{\frac{3}{2}} + C] = -\frac{1}{3} {h}^{\frac{3}{2}} + C = -\frac{1}{3} {(9 - r^2)}^{\frac{3}{2}} + C

Aplicando los límites de esta integral

\displaystyle \int_{2}^{3}{\sqrt{9-r^2} r dr} = \left[ -\frac{1}{3} {(9-r^2)}^{\frac{3}{2}} + C \right]_{2}^{3}

\displaystyle = [-\frac{1}{3} {(9-3^2)}^{\frac{3}{2}} + C] - [-\frac{1}{3} {(9-2^2)}^{\frac{3}{2}} + C] = \frac{1}{3} {(5)}^{\frac{3}{2}}

Continuando

\displaystyle \int_{0}^{\frac{\pi}{2}}{\int_{2}^{3}{\sqrt{9-r^2} r dr} d\theta} = \int_{0}^{\frac{\pi}{2}}{\frac{1}{3} {(5)}^{\frac{3}{2}} d\theta}

\displaystyle = \frac{1}{3} {(5)}^{\frac{3}{2}} \int_{0}^{\frac{\pi}{2}}{d\theta} = \frac{1}{3} {(5)}^{\frac{3}{2}} \left[ \theta \right]_{0}^{\frac{\pi}{2}} = \frac{1}{3} {(5)}^{\frac{3}{2}} (\frac{\pi}{2} - 0)

\displaystyle = \frac{1}{3} {(5)}^{\frac{3}{2}} (\frac{\pi}{2}) = \frac{\pi}{6} {(5)}^{\frac{3}{2}}

Por lo tanto

\displaystyle \therefore \int_{0}^{\frac{\pi}{2}}{\int_{2}^{3}{\sqrt{9 - r^2} r dr d\theta}} = \frac{\pi}{6} {(5)}^{\frac{3}{2}}

Problema 3. Resolver la siguiente integral

\displaystyle \int_{0}^{a}{\int_{0}^{\sqrt{a^2-y^2}}{y dx} dy}

Solución. Aquí se realiza la transformación de coordenadas rectangulares a coordenadas polares. Para ello, con y=r sen θ y los límites inferior y superior son

Así que la integral

\displaystyle \int_{0}^{a}{\int_{0}^{\sqrt{a^2-y^2}}{y dx} dy} = \int_{0}^{\frac{\pi}{2}}{\int_{0}^{a}{r \sin{\theta} r dr}d\theta}

Resolviendo esta transformación

\displaystyle \int_{0}^{\frac{\pi}{2}}{\int_{0}^{a}{r \sin{\theta} r \ dr} d\theta} = \int_{0}^{\frac{\pi}{2}}{\int_{0}^{a}{r^2  \sin{\theta} \ dr} d\theta}

Resolviendo la integral del centro

\displaystyle \int_{0}^{a}{r^2 \sin{\theta} dr} = \sin{\theta} \int_{0}^{a}{r^2 dr} = \sin{\theta} \left[\frac{1}{3} r^3 \right]_{0}^{a} = \sin{\theta}(\frac{1}{3} a^3 - 0) = \frac{1}{3} a^3 \sin{\theta}

Regresando

\displaystyle \int_{0}^{\frac{\pi}{2}}{\int_{0}^{a}{r^2 \sin{\theta} dr} d\theta} = \int_{0}^{\frac{\pi}{2}}{\frac{1}{3} a^3 \sin{\theta} d\theta} = \frac{1}{3} a^3 \int_{0}^{\frac{\pi}{2}}{\sin{\theta} d\theta} = \frac{1}{3} a^3 \left[-\cos{\theta} \right]_{0}^{\frac{\pi}{2}}

\displaystyle = \frac{1}{3} a^3 (-\cos{\frac{\pi}{2}} + \cos{0}) = \frac{1}{3} a^3 (0+1) = \frac{1}{3} a^3 (1) = \frac{1}{3} a^3

Finalmente

\displaystyle \therefore \int_{0}^{a}{\int_{0}^{\sqrt{a^2-y^2}}{y dx} dy} = \frac{1}{3} a^3

Problema 4. Resolver la siguiente integral

\displaystyle \int_{0}^{3}{\int_{0}^{\sqrt{9-y^2}}{{(x^2+y^2)}^{\frac{3}{2}} dx} dy}

Solución. Aquí se realiza la transformación de coordenadas rectangulares a coordenadas polares. Para ello, con x=r \cos{\theta} y y=r \sin{\theta} y los límites inferior y superior son

Si r=3 y y_1=0

\sin{\theta}=0

\theta_1=0

Si r=3 y y_2=3

\sin{\theta} = 1

\displaystyle \theta_2 = \frac{\pi}{2}

Así que la integral

\displaystyle \int_{0}^{3}{\int_{0}^{\sqrt{9-y^2}}{{(x^2+y^2)}^{\frac{3}{2}} dx} dy} = \int_{0}^{\frac{\pi}{2}}{\int_{0}^{3}{[{(r \cos{\theta})}^{2} + {{(r \sin{\theta})}^{2}]}^{\frac{3}{2}} r dr} d\theta}

Resolviendo esta transformación

\displaystyle \int_{0}^{\frac{\pi}{2}}{\int_{0}^{3}{{[{(r \cos{\theta})}^{2} + {(r \sin{\theta})}^{2} ]}^{\frac{3}{2}}  r dr} d\theta} = \int_{0}^{\frac{\pi}{2}}{\int_{0}^{3}{ {[r^2 {({cos}^{2}{\theta} + {\sin}^{2}{\theta})}^{2}]}^{\frac{3}{2}} r dr} d\theta}

\displaystyle = \int_{0}^{\frac{\pi}{2}}{\int_{0}^{3}{r^3 {({\cos}^{2}{\theta} + {\sin}^{2}{\theta})}^{3}  r dr} d\theta} = \int_{0}^{\frac{\pi}{2})}{\int_{0}^{3}{r^4 {({\cos}^{2}{\theta} + {\sin}^{2}{\theta})}^{3} dr} d\theta}

\displaystyle = \int_{0}^{\frac{\pi}{2}}{\int_{0}^{3}{r^4 {(1)}^{3} dr} d\theta} = \int_{0}^{\frac{\pi}{2}}{\int_{0}^{3}{r^4  dr} d\theta}

Resolviendo la integral del centro

\displaystyle \int_{0}^{3}{r^4 \ dr} = \left[\frac{1}{5} r^5 \right]_{0}^{3}

\displaystyle = [\frac{1}{5} {(3)}^{5}] - [\frac{1}{5} {(0)}^{5}] = \frac{243}{5}

Continuando

\displaystyle \int_{0}^{\frac{\pi}{2}}{\int_{0}^{3}{r^4  dr} d\theta} = \int_{0}^{\frac{\pi}{2}}{\frac{243}{5} d\theta}

\displaystyle \int_{0}^{\frac{\pi}{2}}{\int_{0}^{3}{r^4  dr} d\theta} = \frac{243}{5} \int_{0}^{\frac{\pi}{2}}{d\theta} = \frac{243}{5} \left[\theta \right]_{0}^{\frac{\pi}{2}}

\displaystyle \int_{0}^{\frac{\pi}{2}}{\int_{0}^{3}{r^4  dr} d\theta} = \frac{243}{5} (\frac{\pi}{2}-0) = \frac{243}{10} \pi

Por lo tanto

\displaystyle \therefore \int_{0}^{3}{\int_{0}^{\sqrt{9-y^2}}{{(x^2+y^2)}^{\frac{3}{2}} dx} dy} = \frac{243}{10} \pi

Avatar de Desconocido

Publicado por Cesar Reyes

Dedicado a compartir información temas referentes al cálculo básicos, intermedios y avanzados mediante presentaciones PDF, videos y publicaciones en este sitio web.

Deja un comentario

Este sitio utiliza Akismet para reducir el spam. Conoce cómo se procesan los datos de tus comentarios.