Aproximación del área en una región plana. Cálculo integral.

Introducción

Para rectángulos inscritos

$\displaystyle A = \sum_{k=1}^{n}{f({x}_{k-1}) \cdot \Delta x}$

Donde

$\displaystyle f({x}_{k-1}) = (\Delta x)(k - 1)$

*Figura 1. Representación del área bajo la curva usando rectángulos inscritos.*

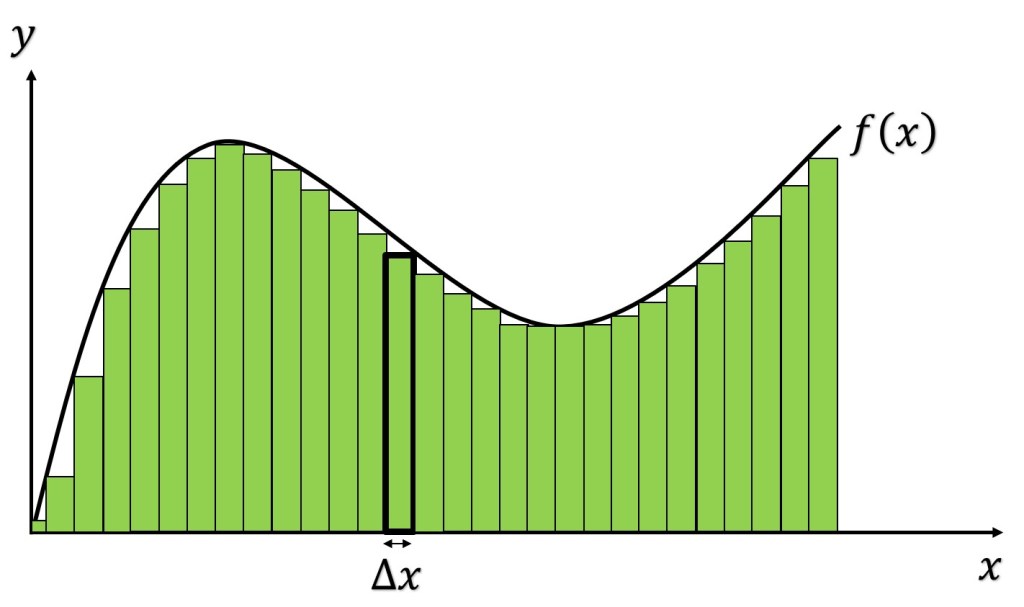
Para rectángulos circunscritos

$\displaystyle A = \sum_{k=1}^{n}{f({x}_{k}) \cdot \Delta x}$

Donde

$\displaystyle f({x}_{k}) = (\Delta x)(k)$

*Figura 2. Representación del área bajo la curva usando rectángulos circunscritos.*

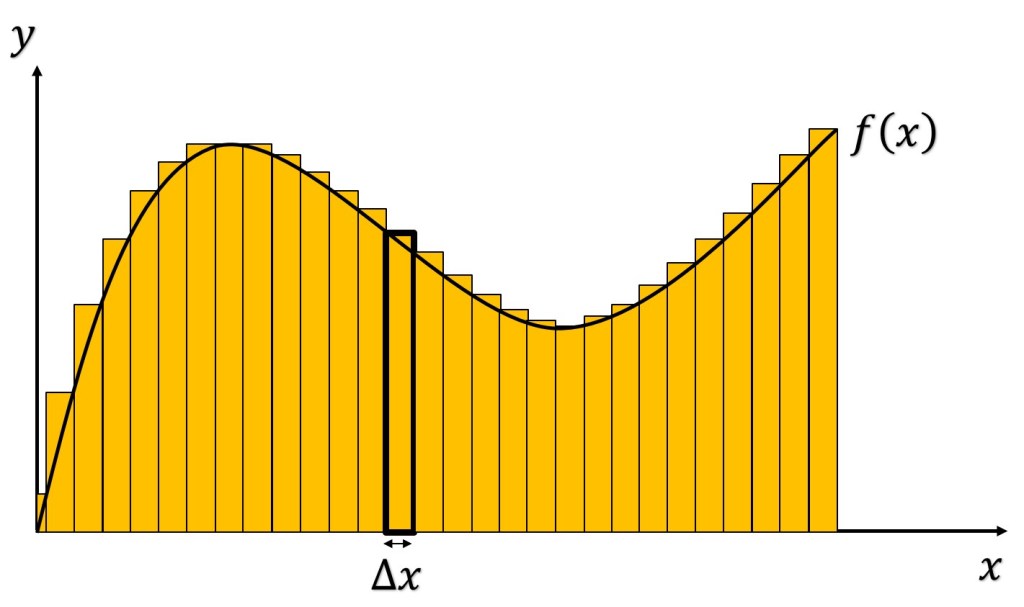
Aproximación del área de una región plana

Su fórmula es la siguiente

$\displaystyle A = \lim_{n \rightarrow \infty} \sum_{k=1}^{n}{f({x}_{k}) \cdot \Delta x}$

Donde

$f(x_k)$ : representa la función dada a la “k-ésima”.
$\Delta x$ : representa el incremento (el tamaño del rectángulo)

Problemas resueltos

Problema 1. Hallar el área para $\displaystyle f(x) = {x}^{2} + 10$ para rectángulos circunscritos e inscritos con para 10 rectángulos y cuando $n \rightarrow \infty$ en un intervalo de [0,8].

Solución. Para rectángulos circunscritos

$\displaystyle A = \sum_{k=1}^{n}{f({x}_{k}) \cdot \Delta x}$

$\displaystyle A= \sum_{k=1}^{n}{({x}^{2}+10)\left(\frac{b-a}{n}\right)} = \sum_{k=1}^{n}{\left\{{\left[\left( \frac{b-a}{n}\right)(k)\right]}^{2}+10\right\} \left(\frac{b-a}{n}\right)}$

$\displaystyle A= \sum_{k=1}^{10}{ \left\{ \left[\left( \frac{8-0}{10} \right)(k)\right]^2+10 \right\} \left(\frac{8-0}{10}\right)} = \sum_{k=1}^{10}{\left\{{\left[\left( \frac{8}{10} \right)(k) \right]}^{2} + 10 \right\} \left( \frac{8}{10}\right)}$

$\displaystyle A= \sum_{k=1}^{10}{\left[ \left(\frac{4}{5} k \right)^2+10 \right] \left(\frac{4}{5}\right)} = \sum_{k=1}^{10}{\left( \frac{16}{25} {k}^{2} + 10 \right) \left(\frac{4}{5} \right)} = \sum_{k=1}^{10}{\left(\frac{64}{125} {k}^{2}+8 \right)}$

$\displaystyle A= \sum_{k=1}^{10}{\frac{64}{125} {k}^{2}} + \sum_{k=1}^{10}{8} = \frac{64}{125} \sum_{k=1}^{10}{{k}^{2}} +8 \sum_{k=1}^{10}{1}$

$\displaystyle A= \frac{64}{125} \left[\frac{10(10+1)(20+1)}{6} \right] + 8(10) = \frac{64}{125} \left[\frac{10(11)(21)}{6} \right] + 80$

$\displaystyle A = \frac{64}{125} \left(\frac{2310}{6} \right) + 80 = \frac{147840}{750} + 80 = \frac{6928}{25} {u}^{2}$

$\displaystyle \therefore A = \frac{6928}{25} {u}^{2}$

Para rectángulos inscritos

$\displaystyle A = \sum_{k=1}^{n}{f({x}_{k-1}) \cdot \Delta x}$

$\displaystyle A = \sum_{k=1}^{n}{\left({x}^{2}+10 \right) \left(\frac{b-a}{n} \right)} = \sum_{k=1}^{n}{ \left[ \left[ \left(\frac{b-a}{n}\right)(k-1) \right]^{2}+10 \right] \left(\frac{b-a}{n}\right)}$

$\displaystyle A = \sum_{k=1}^{10}{\left[ {\left[ \left( \frac{8-0}{10} \right)(k-1) \right]}^{2}+10 \right] \left(\frac{8-0}{10}\right)} = \sum_{k=1}^{10}{\left[ {\left[ \left(\frac{8}{10} \right)(k-1)\right]}^{2}+10 \right] \left(\frac{8}{10}\right)}$

$\displaystyle A = \sum_{k=1}^{10}{ \left[ \left( \frac{64}{100} (k^2-2k+1) \right) + 10 \right] \left( \frac{8}{10}\right)} = \sum_{k=1}^{10}{ \left[ \left( \frac{512}{1000} (k^2-2k+1) \right)+8 \right]}$

$\displaystyle A = \frac{64}{125} \sum_{k=1}^{10}{{k}^{2}} - \frac{128}{125} \sum_{k=1}^{10}{k} + \frac{64}{125} \sum_{k=1}^{10}{1} + 8\sum_{k=1}^{10}{1}$

$\displaystyle A = \frac{64}{125} \left[ \frac{10(10+1)(20+1)}{6} \right] - \frac{128}{25} \left[ \frac{10(10+1)}{2} \right] + \frac{64}{125}(10) + 8(10)$

$\displaystyle A= \frac{64}{125}{\left[ \frac{10(11)(21)}{6} \right]} - \frac{128}{125} \left[\frac{10(11)}{2} \right] + \frac{640}{125} + 80$

$\displaystyle A= \left( \frac{64}{125} \right) \left( \frac{2310}{6} \right) - \left(\frac{14080}{250}\right) + \frac{640}{125} + 80$

$\displaystyle A= \frac{147840}{750} - \frac{14080}{250} + \frac{640}{125} + 80 = \frac{5648}{25} {u}^{2}$

$\displaystyle \therefore A = \frac{5648}{25} {u}^{2}$

Cuando se tienen los resultados del área con rectángulos circunscritos y del área con rectángulos inscritos, se obtiene un intervalo

área inscrita < A < área circunscrita

$\displaystyle \frac{5128}{25} {\text{u}}^{2} < A < \frac{6928}{25} {\text{u}}^{2}$

Dentro de ese intervalo se ubica el área aproximada de la función “ $x^2 + 10$ ”. Para saberlo, se utilizará la fórmula de aproximación del área de la región plana

$\displaystyle A = \lim_{n \rightarrow \infty} \sum_{k=1}^{n}{f({x}_{k}) \cdot \Delta x}$

Donde el intervalo a tomar seguirá siendo [2,10] y con la misma función « $x^2 + 10$ «.

$\displaystyle A = \lim_{n \rightarrow \infty} \sum_{k=1}^{n}{\left({x}^{2}+10\right) \left( \frac{b-a}{n} \right)} = \lim_{n \rightarrow \infty} \sum_{k=1}^{n}{\left[ \left[ \left(\frac{b-a}{n} \right)(k) \right]^2+10 \right] \left( \frac{b-a}{n} \right)}$

$\displaystyle A= \lim_{n \rightarrow \infty} \sum_{k=1}^{n}{ \left[ \left(\frac{8- 0}{n} \right)(k) \right]^2 + 10] \left( \frac{8 - 0}{n} \right)} = \lim_{n \rightarrow \infty} \sum_{k=1}^{n}{\left[ {\left[ \left(\frac{8}{n} \right)(k) \right]}^{2} + 10 \right] \left(\frac{8}{n} \right)}$

$\displaystyle A= \lim_{n \rightarrow \infty} \sum_{k=1}^{n}{\left[ \left(\frac{64}{{n}^{2}} {k}^{2}\right)+10 \right] \left(\frac{8}{n}\right)} = \lim_{n \rightarrow \infty} \sum_{k=1}^{n}{\left( \frac{512}{{n}^{3}}{k}^{2}+\frac{80}{n}\right)}$

$\displaystyle A= \lim_{n \rightarrow \infty}{\left( \frac{512}{{n}^{3}} \sum_{k=1}^{n}{k}^{2} + \frac{80}{n} \sum_{k=1}^{n}{1} \right)} = \lim_{n \rightarrow \infty} {\left\{ \frac{512}{{n}^{3}} \left[ \frac{n(n+1)(2n+1)}{6} \right] + \frac{80}{n} (n) \right\}}$

$\displaystyle A = \lim_{n \rightarrow \infty}{\left\{\frac{512}{{n}^{3}} \left[ \frac{({n}^{2} +n)(2n+1)}{6} \right] + 80\right\}} = \lim_{n \rightarrow \infty}{\left[ \frac{512}{{n}^{3}} \left(\frac{2{n}^{3}+3{n}^{2} + n}{6} \right) + 80 \right]}$

$\displaystyle A = \lim_{n \rightarrow \infty}{ \left[\frac{512}{6} \left( \frac{2n^3+3n^2 + n}{n^3} \right) + 80 \right]} = \lim_{n \rightarrow \infty}{\left[ \frac{512}{6} \left(2 + \frac{3}{n} + \frac{1}{n^2} \right) + 80 \right]}$

$\displaystyle A = \left( \frac{512}{6} \right) \lim_{n \rightarrow \infty}{\left(2 + \frac{3}{n} + \frac{1}{n^2} \right)} + \lim_{n \rightarrow \infty}{(80)} = \frac{512}{3} + 80 = \frac{752}{3}$