Conversión de base 10 a base 2. Métodos numéricos.

Problemas resueltos

Problema 1. Convertir el número 77 expresado en base 10 a base 2.

$\displaystyle {(77)}_{10} = {( \quad \quad \quad )}_{2}$

Solución. Se divide el número brindado por el problema (dividendo) entre la base requerido (divisor); en este caso, se divide 77 entre 2. Del resultado que se obtenga, nuevamente, se divide entre dos. Durante la división, el cociente debe ser un valor entero, así que, es importante observar si entre el dividendo y el divisor genera residuos, ya que estos también forman parte de la solución del problema. El procedimiento de la división culmina hasta que el último cociente muestre un valor unitario.

Tomando el último resultado del cociente (es decir 1,) seguido del último residuo (es decir, 0) y finalmente se toman los residuos restantes en forma ascendente (es decir, 0, 1, 1, 0 y 1). Por tanto, el número binario esperado es 1 0 0 1 1 0 1.

$\displaystyle \therefore {(77)}_{10} = {(1001101)}_{2}$

Problema 2. Convertir el número 47 expresado en base 10 a base 2.

$\displaystyle {(47)}_{10} = {(\quad \quad \quad )}_{2}$

Solución. Se divide el número brindado por el problema (dividendo) entre la base requerido (divisor); en este caso, se divide 47 entre 2. Del resultado que se obtenga, nuevamente, se divide entre dos. Durante la división, el cociente debe ser un valor entero, así que, es importante observar si entre el dividendo y el divisor genera residuos, ya que estos también forman parte de la solución del problema. El procedimiento de la división culmina hasta que el último cociente muestre un valor unitario.

Tomando el último resultado del cociente (es decir 1,) seguido del último residuo (es decir, 0) y finalmente se toman los residuos restantes en forma ascendente (es decir, 1, 1, 1 y 1). Por tanto, el número binario esperado es 1 0 1 1 1 1.

$\displaystyle \therefore {(47)}_{10} = {(101111)}_{2}$

Problema 3. Convertir el número 631 expresado en base 10 a base 2.

$\displaystyle {(631)}_{10} = {(\quad \quad \quad )}_{2}$

Solución. Se divide el número brindado por el problema (dividendo) entre la base requerido (divisor); en este caso, se divide 631 entre 2. Del resultado que se obtenga, nuevamente, se divide entre dos. Durante la división, el cociente debe ser un valor entero, así que, es importante observar si entre el dividendo y el divisor genera residuos, ya que estos también forman parte de la solución del problema. El procedimiento de la división culmina hasta que el último cociente muestre un valor unitario.

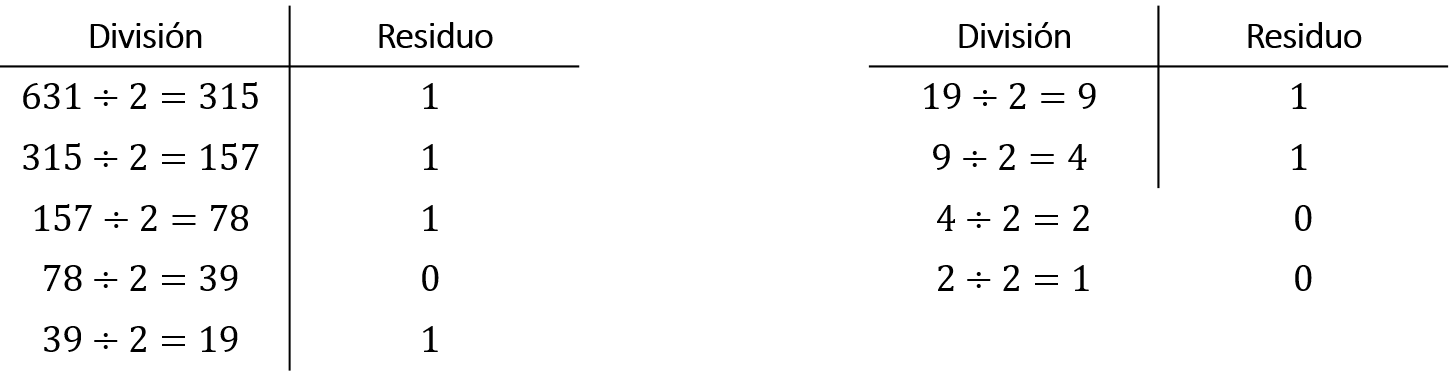
Tomando el último resultado del cociente (es decir 1,) seguido del último residuo (es decir, 0) y finalmente se toman los residuos restantes en forma ascendente (es decir, 0, 1, 1, 1, 0, 1, 1, 1 y 1). Por tanto, el número binario es 1 0 0 1 1 1 0 1 1 1.

$\displaystyle \therefore {(631)}_{10} = {(1 0 0 1 1 1 0 1 1 1)}_{2}$

Problema 4. Convertir el número 13.875 expresado en base 10 a base 2.

$\displaystyle {(13.875)}_{10} = {( \quad \quad \quad )}_{2}$

Solución. Este problema se resuelve en dos partes por que el número presenta valores enteros y valores decimales. Comenzando a resolver con la parte entera

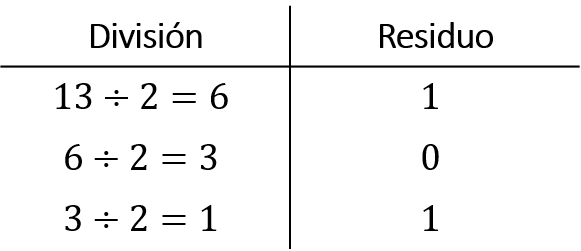
Tomando el último resultado del cociente (es decir 1,) seguido del último residuo (es decir, 1) y finalmente se toman los residuos restantes en forma ascendente (es decir, 0 y 1). Por tanto, la parte entera, tiene un número binario de 1 1 0 1.

Por último, en la parte decimal, se toma solo la parte decimal del problema haciendo que el entero tenga un valor de cero y se hace la multiplicación de ese número por la base a convertir, es decir, multiplicar 0.875 por 2; del resultado que muestre se extrae todo los decimales y se vuelve a multiplicar por la base requerida. Este procedimiento termina hasta una cierta cantidad de iteraciones necesarias, o también, si en el procedimiento muestra ceros después del punto.

$\displaystyle 0.875 \times 2 = 1.750$

$\displaystyle 0.750 \times 2 = 1.500$

$\displaystyle 0.500 \times 2 = 1.000$

Como este último resultado muestra ceros después del punto, aquí termina la multiplicación. La respuesta en la parte decimal consiste en tomar todos los valores enteros obtenidos en cada producto en forma descendente, es decir, 1 1 1. Finalmente, uniendo los resultados de la parte entera y la parte decimal, el número binario es

$\displaystyle \therefore {(13.875)}_{10} = {(1101.111)}_{2}$

Problema 5. Convertir el número 51.227 expresado en base 10 a base 2.

$\displaystyle {(51.227)}_{10} = {( \quad \quad \quad )}_{2}$

Solución. Este problema se resuelve en dos partes, por que el número presenta valores enteros y valores decimales. Comenzando a resolver con la parte entera

Tomando el último resultado del cociente (es decir 1,) seguido del último residuo (es decir, 1) y finalmente se toman los residuos restantes en forma ascendente (es decir, 0, 0, 1 y 1). Por tanto, en la parte entera, el número binario es 1 1 0 0 1 1.

Por último, en la parte decimal, se toma solo la parte decimal del problema haciendo que el entero tenga un valor de cero y se hace la multiplicación de esa número por la base a convertir, es decir, multiplicar 0.227 por 2; del resultado que muestre se extrae todo los decimales y se vuelve a multiplicar por la base requerida. Este procedimiento termina hasta una cierta cantidad de iteraciones necesarias, o también, si en el procedimiento muestra ceros después del punto.

$\displaystyle 0.227 \times 2 = 0.454$

$\displaystyle 0.454 \times 2=0.908$

$\displaystyle 0.908 \times 2=1.816$

$\displaystyle 0.816 \times 2 = 1.632$

$\displaystyle 0.632 \times 2=1.264$

Como este último resultado no muestra ceros después del punto, se va a considerar sólo cinco iteraciones, por tanto, aquí termina la multiplicación. La respuesta en la parte decimal consiste en tomar todos los valores enteros obtenidos en cada producto en forma descendente, es decir, 0 0 1 1 1. Finalmente, uniendo los resultados de la parte entera y la parte decimal, el número binarios es

$\displaystyle \therefore {(51.227)}_{10} = {(110011.00111)}_{2}$

Si se desea conocer cuanta diferencia puede haber entre el resultado final y el valor del problema, solo basta realizar una resta. Para hacerlo, solo basta con convertir el resultado final de base 2 a base 10; de la parte entera, del punto decimal hacia la izquierda, se multiplica cada dígito por la base convertida elevado una potencia aumentada unitariamente (partiendo del cero, 0) y, de la parte decimal, del punto decimal hacia la derecha, se multiplica cada dígito por la base convertida elevado a una potencia disminuida unitariamente (partiendo del menos uno, -1). A continuación, el procedimiento mencionado

$\displaystyle {(110011.00111)}_{2} = (1 \times 2^5 )+(1 \times 2^4 )+(0 \times 2^3 )+(0 \times 2^2 )+(1 \times 2^1 )+(1 \times 2^0 ) + (0 \times 2^{-1} )+(0 \times 2^{-2} )+(1 \times 2^{-3} )+(1 \times 2^{-4} )+(1 \times 2^{-5} )$

$\displaystyle {(110011.00111)}_{2} = 32+16+0+0+2+1+0+0+0.125+0.0625+0.03125$

$\displaystyle \therefore {(110011.00111)}_{2} = {(51.21875)}_{10}$

El resultado de la diferencia del valor exacto (número brindado por el problema) y el valor aproximado (resultado final del problema) se denomina error. Entonces, el error es igual a

$\displaystyle E = |V.E.-V.A.|=|51.227-51.21875|$

$\displaystyle E=0.00825$

Se concluye que entre el resultado final y el valor del problema solo existe una diferencia del 0.00825, lo cual, es un valor tolerable.

Problema 6. Convertir el número 89.35 expresado en base 10 a base 4 para tres iteraciones

$\displaystyle {(89.35)}_{10} = {( \quad \quad \quad )}_{4}$

Solución. De la parte entera, se divide el número brindado por el problema (dividendo) entre la base requerido (divisor); en este caso, se divide 89 entre 4. Del resultado que se obtenga, nuevamente, se divide entre dos. Durante la división, el cociente debe ser un valor entero, así que, es importante observar si entre el dividendo y el divisor genera residuos, ya que estos también forman parte de la solución del problema. El procedimiento de la división culmina hasta que el último cociente tenga un resultado menor del valor de la base requerida

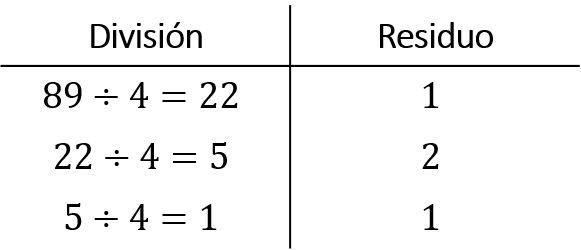
Tomando el último resultado del cociente (es decir 1,) seguido del último residuo (es decir, 1) y finalmente se toman los residuos restantes en forma ascendente (es decir, 2 y 1). Por tanto, en la parte entera, el número binario es 1 1 2 1.

Por último, en la parte decimal, se toma solo la parte decimal del problema haciendo que el entero tenga un valor de cero y se hace la multiplicación de esa cifra por la base a convertir, es decir, multiplicar 0.350 por 4; del resultado que muestre se extrae todo los decimales y se vuelve a multiplicar por la base requerida. Este procedimiento termina hasta una cierta cantidad de iteraciones necesarias, o también, si en el procedimiento muestra ceros después del punto.

$\displaystyle 0.350 \times 4=1.400$

$\displaystyle 0.400 \times 4=1.600$

$\displaystyle 0.600 \times 4=2.400$

Como este último resultado no muestra ceros después del punto, se va a considerar sólo tres iteraciones, por tanto, aquí termina la multiplicación. La respuesta en la parte decimal consiste en tomar todos los valores enteros obtenidos en cada producto en forma descendente, es decir, 1 1 2. Finalmente, uniendo los resultados de la parte entera y la parte decimal, el número binario es

$\displaystyle \therefore {(89.35)}_{10} = {(1121.112)}_{4}$

Si se desea conocer cuanta diferencia puede haber entre el resultado final y el valor del problema, solo basta realizar una resta. Para hacerlo, solo basta con convertir el resultado final de base 4 a base 10; de la parte entera, del punto decimal hacia la izquierda, se multiplica cada dígito por la base convertida elevado una potencia aumentada unitariamente (partiendo del cero, 0) y, de la parte decimal, del punto decimal hacia la derecha, se multiplica cada dígito por la base convertida elevado a una potencia disminuida unitariamente (partiendo del menos uno, -1). A continuación, el procedimiento mencionado

$\displaystyle {(1121.112)}_{2} = (1 \times 4^3 )+(1 \times 4^2 )+(2 \times 4^1 )+(1 \times 4^0 )+(1 \times 4^{-1} )+(1 \times 4^{-2} )+(2 \times 4^{-3} )$

$\displaystyle {(1121.112)}_{2} = 64+16+8+1+0.25+0.0625+0.03125$

$\displaystyle \therefore {(1121.112)}_{2} = {(89.34375)}_{10}$

El resultado de la diferencia del valor exacto (número brindado por el problema) y el valor aproximado (resultado final del problema) se denomina error. Entonces, el error es igual a

$\displaystyle E=|V.E.-V.A.|=|89.35-89.34375|$

$\displaystyle E=0.00625$

Se concluye que entre el resultado final y el valor del problema solo existe una diferencia del 0.00625, lo cual, es un valor tolerable.

Problema 7. Convertir el número 11001110.1010 expresado en base 2 a base 10.

$\displaystyle {(11001110.1010)}_{2} = {( \quad \quad \quad )}_{10}$

Solución. Del punto decimal hacia la izquierda, se multiplica cada dígito por la base elevado una potencia aumentada unitariamente (partiendo del cero, 0) y, de la parte decimal, del punto decimal hacia la derecha, se multiplica cada dígito por la base elevado a una potencia disminuida unitariamente (partiendo del menos uno, -1). Entonces

$\displaystyle {(11001110.1010)}_{2} = (1 \times 2^7 )+(1 \times 2^6 )+(0 \times 2^5 )+(0 \times 2^4 )+(1 \times 2^3 )+(1 \times 2^3 )+(1 \times 2^1 )+(0 \times 2^0 )+(1 \times 2^{-1} )+(0 \times 2^{-2} )+(1 \times 2^{-3} )+(0 \times 2^{-4} )$