¿Cómo identificar una o varias raíces en una función dada?. Métodos numéricos.

Introducción

Métodos abiertos

$\displaystyle x_0 = \frac{a+b}{2}$

Métodos cerrados

$[x_0 , x_1 ]$

Problemas resueltos

Problema 1. Para la función $x^2 - 3x - 5 = 0$ , determinar sus raíces positivas y negativas.

Solución. Se lleva a cabo una tabulación en donde se empieza a tomar el valor de «x» de -3.

Por lo tanto, la función $x^2 - 3x - 5 = 0$ presenta dos cambios de signo (raíces) cuando $x = -2$ y $x = -1$ .

Problema 2. Para la función $\displaystyle e^x + 5 = 0$ , determinar sus raíces positivas y negativas.

Solución. Se elabora una tabulación donde el valor de «x» empieza a partir de -3 hasta $x=3$ .

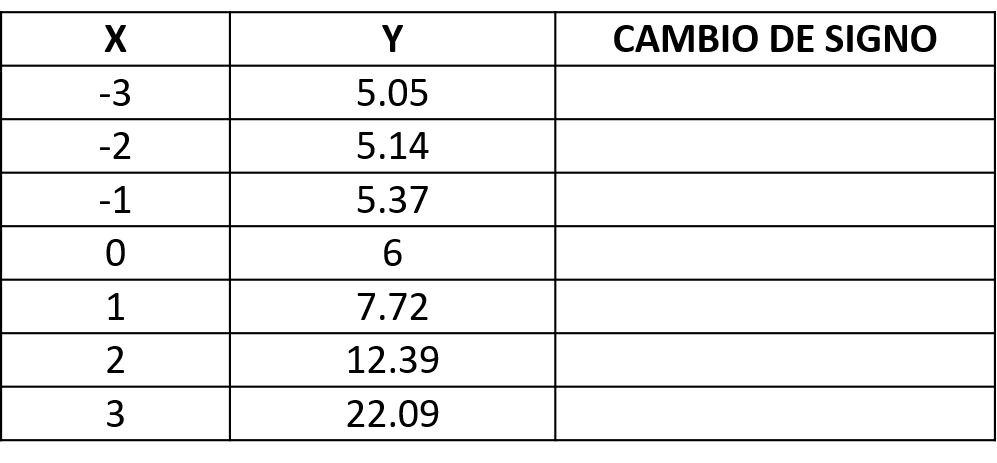
Por lo tanto, la función $e^x + 5 = 0$ no presenta cambios de signo.

Problema 3. Para la función $e^x - 3 = 0$ , determinar sus raíces positivas y negativas.

Solución. Se elabora una tabulación donde el valor de «x» comienza a partir de -2 y termina hasta 2.

Por lo tanto, la función $e^x - 3 = 0$ presenta cambio de signo cuando $x=1$ y $x=2$ .

Problema 4. Para la función $\sin{2x} + 2 = 0$ , determinar sus raíces positivas y negativas.

Solución. Se elabora una tabulación donde el valor de «x» comienza de 90° y culmina hasta -90°.

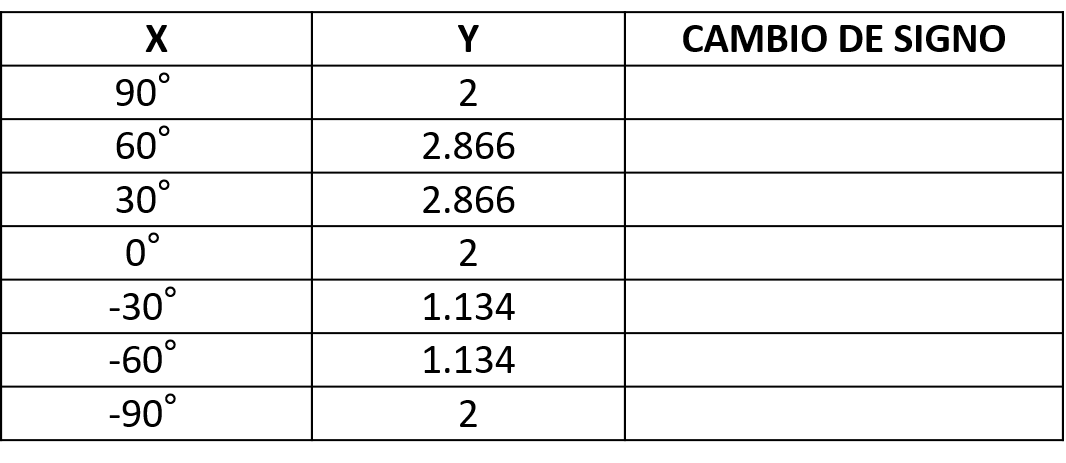
Por lo tanto, la función $\sin{2x} + 2 = 0$ no presenta cambios de signo.

Publicado por Cesar Reyes

Dedicado a compartir información temas referentes al cálculo básicos, intermedios y avanzados mediante presentaciones PDF, videos y publicaciones en este sitio web. Ver todas las entradas de Cesar Reyes

Deja un comentario Cancelar la respuesta

Este sitio utiliza Akismet para reducir el spam. Conoce cómo se procesan los datos de tus comentarios.