Método de aproximaciones sucesivas. Primer método abierto. Métodos numéricos.

Introducción

De una función $y = f(x)$ , igualándola a cero

$f(x) = 0$

Donde, la función $f(x)$ presenta al menos una raíz (cambio de signo) y a partir de allí se obtiene la solución aproximada (punto medio).

$x = x_0$

De la función $f(x)$ se despeja la variable «x» sólo una parte, quedando de la siguiente manera

$x = q(x)$

Sustituyendo $x = x_0$ en $q(x)$ , se obtiene $x_1$

$x_1 = q(x_0 )$

Y el primer error, $E_1$ , es

$E_1 = |x_1 - x_0 |$

Sustituyendo $x = x_1$ en $q(x)$ , se obtiene $x_2$

$x_2 = q(x_1 )$

Y el segundo error, $E_2$ , es

$E_2 = |x_2 - x_1 |$

Sustituyendo $x = x_2$ en $q(x)$ , se obtiene $x_3$

$x_3 = q(x_2 )$

Y el tercer error, $E_3$ , es

$E_3 = |x_3 - x_2 |$

Sustituyendo $x = x_n$ en $q(x)$ , se obtiene ${x}_{n+1}$

${x}_{n+1} = q(x_n )$

Y el «n» error, $E_n$ , es

${E}_{n+1} = |{x}_{n+1} - x_n |$

Donde $n = 0, 1, 2, ...$

Problemas resueltos

Problema 1. Encontrar la raíz positiva para $x^2 - 3x = 8$ con tolerancia de $1 \times {10}^{-2} = 0.01$ .

Solución. Se elabora una tabulación donde los valores de «x» serán positivos, comenzado a partir de $x=0$ .

En la tabulación, la función presenta un cambio de signo, entre x=4 y x=5. Entonces, los valores son a=4 y b=5.

Se calcula el punto medio

$\displaystyle x_0 = \frac{b+a}{n}$

$\displaystyle x_0 = \frac{5+4}{2} = \frac{9}{2}$

$x_0 = 4.5$

De la función dada, se despeja una variable $x$

$x^2 - 3x = 8$

$x^2 = 3x + 8$

$\displaystyle x = \pm \sqrt{3x+8}$

$\displaystyle x = \sqrt{3x+8}$

La función a usar es

$\displaystyle q(x) = \sqrt{3x+8}$

En la primera iteración, $x_0 = 4.5$

$\displaystyle x_1 = q(x_0 )$

$\displaystyle x_1 = q(4.5) = \sqrt{3(4.5)+8} = \sqrt{21.5}$

$x_1 = 4.637$

El primer error es

$E_1 = |x_1 - x_0 |$

$E_1 = |4.637 - 4.5| = |0.137|$

$E_1 = 0.137$

Comparando el valor de $E_1$ con el valor de la tolerancia

$0.137 > 0.01$

Este error es mayor que la tolerancia deseada por lo que se pasa a la siguiente iteración. En la segunda iteración, se utiliza el valor de $x_1$ .

$\displaystyle x_2 = q(x_1 ) = q(4.637)$

$\displaystyle x_2 = \sqrt{3(4.5)+8} = \sqrt{21.5}$

$x_2 = 4.681$

El segundo error es

$E_2 = |x_2 - x_1 |$

$E_2 = |4.681 - 4.637| = |0.044|$

$E_2 = 0.044$

Comparando con el valor de $E_2$ con el valor de la tolerancia

$0.044 > 0.01$

Este error es mayor que la tolerancia deseada por lo que se pasa a la siguiente iteración. En la tercera iteración, sustituyendo el valor de $x_2$

$\displaystyle x_3 = q(x_2 ) = q(4.681)$

$\displaystyle x_3 = \sqrt{3(4.681)+8} = \sqrt{22.043}$

$x_3 = 4.695$

El tercer error es

$E_3 = |x_1 - x_0 |$

$E_3 = |4.695 - 4.681|=|0.014|$

$E_3 = 0.014$

Comparando con el valor de $E_3$ con el valor de la tolerancia

$0.014 > 0.01$

Este error es mayor que la tolerancia por lo que se pasa a la siguiente iteración. En la cuarta iteración se utiliza el valor de $x_3$

$\displaystyle x_4 = q(x_3 ) = q(4.695)$

$\displaystyle x_4 = \sqrt{3(4.695)+8} = \sqrt{22.085}$

$x_4 = 4.699$

El cuarto error es

$E_4 = |x_4 - x_3 |$

$E_4 = |4.699 - 4.695| = |0.004|$

$E_4 = 0.004$

Comparando con el valor de $E_4$ con el valor de la tolerancia

$0.004 < 0.01$

Este error es menor que la tolerancia. Por lo tanto, la raíz encontrada es

$\therefore x = 4.699$

Problema 2. Encontrar las raíces para $5x^2 - e^x = 0$ con tolerancia de $1 \times 10^{-3} = 0.001$ .

Solución. Se elabora una tabulación tomando en cuenta primero los valores negativos de «x», luego el cero, y finalmente, los valores positivos; comenzando a partir de $x=-3$ hasta $x=3$ .

La función presenta tres cambios de signo, entre x=-1 y x=0, entre x=0 y x=1, y entre x=4 y x=5.

Para $[-1 , 0]$ , el valor de $x_0$ es

$\displaystyle x_0 = \frac{b+a}{n}$

$\displaystyle x_0 = \frac{0+(-1)}{2} = -\frac{1}{2}$

$x_0 = - 0.5$

De la función del problema, se despeja una variable «x» y estará ubicado en el primer miembro mientras que lo restante se coloca en el segundo miembro

$5x^2 - e^x = 0$

$5x^2 = e^x$

$\displaystyle x = \pm \sqrt{\frac{e^x}{5}} = - \sqrt{\frac{e^{-x}}{5}}$

$\displaystyle q(x) = - \sqrt{\frac{e^x}{5}}$

En la primera iteración (con $x_0 = -0.5$ )

$\displaystyle x_1 = q(x_0 ) = q(-0.5)$

$\displaystyle x_1 = -\sqrt{\frac{e^{-0.5}}{5}}$

$x_1 = -0.348$

El primer error es

$E_1 = |x_1 - x_0 |$

$E_1 = |(-0.348) - (-0.5)| = |-0.348 + 0.5| = |0.152|$

$E_1 = 0.152$

Comparando con el valor de $E_1$ con el valor de la tolerancia

$0.152 > 0.001$

Este error es mayor que la tolerancia, por lo que, se pasa a la segunda iteración (con $x_1 = -0.348$ ), y es

$\displaystyle x_2 = q(x_1 ) = q(-0.348)$

$\displaystyle x_2 = -\sqrt{\frac{e^{-0.348}}{5}}$

$x_2 = -0.376$

El segundo error es

$E_2 = |x_2 - x_1 |$

$E_2 = |(-0.376) - (-0.348)| = |-0.376+0.348| = |-0.028|$

$E_2 = 0.028$

Comparando con el valor de $E_2$ con el valor de la tolerancia

$0.028 > 0.01$

En la tercera iteración (con $x_2 = -0.376$ )

$\displaystyle x_3 = q(x_2 ) = q(-0.376)$

$\displaystyle x_3 = -\sqrt{\frac{e^{-0.376}}{5}}$

$x_3 = -0.371$

El tercer error es

$E_3 = |x_3 - x_2 |$

$E_3 = |(-0.371) - (-0.376)| = |-0.371+0.376| = |0.005|$

$E_3 = 0.005$

Comparando con el valor de $E_3$ con el valor de la tolerancia

$0.005 > 0.001$

En la cuarta iteración (con $x_3 = -0.371$ )

$\displaystyle x_4 = q(x_3 ) = q(-0.371)$

$\displaystyle x_4 = -\sqrt{\frac{e^{-0.371}}{5}}$

$x_4 = -0.371$

El cuarto error es

$E_4 = |x_4 - x_3 |$

$E_4 = |(-0.371) - (-0.371)| = |-0.371+0.371| = |0|$

$E_4 = 0$

Comparando con el valor de $E_4$ con el valor de la tolerancia

$0 < 0.001$

El error ya es menor que la tolerancia, por lo que, el último valor calculado (cuarta iteración, $x_4$ ) es el indicado para el intervalo [-1,0]. Finalmente

$\therefore x = -0.371$

Para $[0 , 1]$ , el valor de $x_0$ es

$\displaystyle x_0 = \frac{b+a}{n}$

$\displaystyle x_0 = \frac{1+0}{2} = \frac{1}{2}$

$x_0 = 0.5$

Utilizando la ecuación despejada que fue obtenida en el intervalo [-1,0]

$\displaystyle q(x) = +\sqrt{\frac{e^x}{5}} = \sqrt{\frac{e^x}{5}}$

En la primera iteración (con $x_0 = 0.5$ ) es

$x_1 = q(x_0 ) = q(0.5)$

$x_1 = \sqrt{\frac{e^{0.5}}{5}}$

$x_1 = 0.574$

El primer error es

$E_1 = |x_1 - x_0 |$

$E_1 = |0.574 - 0.5| = |0.074|$

$E_1 = 0.074$

Comparando con el valor de $E_1$ con el valor de la tolerancia

$0.074 > 0.001$

En la segunda iteración (con $x_1 = 0.574$ ) es

$\displaystyle x_2 = q(x_1 ) = q(0.574)$

$\displaystyle x_2 = \sqrt{\frac{e^{0.574}}{5}}$

$x_2 = 0.596$

El segundo error es

$E_2 = |x_2 - x_1 |$

$E_2 = |0.596 - 0.574| = |0.022|$

$E_2 = 0.022$

Comparando con el valor de $E_2$ con el valor de la tolerancia

$0.022 > 0.001$

La tercera iteración (con $x_2 = 0.596$ ) es

$x_3 = q(x_2 ) = q(0.596)$

$x_3 = \sqrt{\frac{e^{0.596}}{5}}$

$x_3 = 0.602$

El tercer error es

$E_3 = |x_3 - x_2 |$

$E_3 = |0.602 - 0.596| = |0.006|$

$E_3 = 0.006$

Comparando con el valor de $E_3$ con el valor de la tolerancia

$0.006 > 0.001$

La cuarta iteración (con $x_3 = 0.602$ ) es

$\displaystyle x_4 = q(x_3 ) = q(0.602)$

$\displaystyle x_4 = \sqrt{\frac{e^{0.602}}{5}}$

$x_4 = 0.604$

El cuarto error es

$E_4 = |x_4 - x_3 |$

$E_4 = |0.604 - 0.602| = |0.002|$

$E_4 = 0.002$

Comparando con el valor de $E_4$ con el valor de la tolerancia

$E_4 > Tolerancia$

La quinta iteración (con $x_4 = 0.604$ ) es

$\displaystyle x_5 = q(x_5 ) = q(0.604)$

$\displaystyle x_5 = \sqrt{\frac{e^{0.604}}{5}}$

$x_5 = 0.605$

El quinto error es

$E_5 = |x_5 - x_4 |$

$E_5 = |0.605 - 0.604| = |0.001|$

$E_5 = 0.001$

Comparando con el valor de $E_5$ con el valor de la tolerancia

$E_5 = \text{Tolerancia}$

$0.001 = 0.001$

Como el error ya es igual que la tolerancia, el último valor de «x» es el indicado (es decir, $x_5$ )

$\therefore x = 0.605$

Para $[4 , 5]$ , el valor de $x_0$ es

$\displaystyle x_0 = \frac{b+a}{2}$

$\displaystyle x_0 = \frac{5+4}{2} = \frac{9}{2}$

$x_0 = 4.5$

Se toma función despejada obtenida en el intervalo $[-1,0]$

$\displaystyle q(x) = +\sqrt{\frac{e^x}{5}} = \sqrt{e^x/5}$

Para la primera iteración (con $x_0 = 4.5$ ) es

$\displaystyle x_1 = q(x_0 ) = q(4.5)$

$\displaystyle x_1 = \sqrt{\frac{e^{4.5}}{5}}$

$x_1 = 4.243$

El primer error es

$E_1 = |x_1 - x_0 |$

$E_1 = |4.243 - 4.5| = |-0.257|$

$E_1 = 0.257$

Comparando con el valor de $E_1$ con el valor de la tolerancia

$0.257 > 0.001$

La segunda iteración (con $x_1 = 4.243$ ) es

$\displaystyle x_2 = q(x_1 ) = q(4.243)$

$\displaystyle x_2 = \sqrt{\frac{e^{4.243}}{5}}$

$x_2 = 3.731$

El segundo error es

$E_2 = |x_2 - x_1 |$

$E_2 = |3.731 - 4.243| = |-0.512|$

$E_2 = 0.512$

Comparando con el valor de $E_2$ con el valor de la tolerancia

$0.512 > 0.001$

La tercera iteración

$\displaystyle x_3 = q(x_2 ) = q(3.731)$

$\displaystyle x_3 = \sqrt{\frac{e^{3.731}}{5}}$

$x_3 = 2.889$

El tercer error es

$E_3 = |x_3 - x_2 |$

$E_3 = |2.889 - 3.731| = |0.842|$

$E_3 = 0.842$

Comparando con el valor de $E_3$ con el valor de la tolerancia

$0.842 > 0.001$

La cuarta iteración (con $x_3 = 2.889$ ) es

$x_4 = q(x_3 ) = q(2.889)$

$\displaystyle x_4 = \sqrt{\frac{e^{2.889}}{5}}$

$x_4 = 1.891$

El cuarto error es

$E_4 = |x_4 - x_3 |$

$E_4 = |1.891 - 2.889| = |0.998|$

$E_4 = 0.998$

Comparando con el valor de $E_4$ con el valor de la tolerancia

$0.998 > 0.001$

La quinta iteración (con $x_5 = 1.891$ ) es

$\displaystyle x_5 = q(x_5 ) = q(1.891)$

$\displaystyle x_5 = \sqrt{\frac{e^{1.891}}{5}}$

$x_5 = 1.151$

El quinto error es

$E_5 = |x_5 - x_4 |$

$E_5 = |1.151 - 1.891| = |-0.74|$

$E_5 = 0.74$

Comparando con el valor de $E_5$ con el valor de la tolerancia

$0.74 > 0.001$

La sexta iteración (con $x_5 = 1.151$ ) es

$\displaystyle x_6 = q(x_6 ) = q(1.151)$

$\displaystyle x_6 = \sqrt{\frac{e^{1.151}}{5}}$

$x_6 = 0.795$

El sexto error es

$E_6 = |x_6 - x_5 |$

$E_6 = |0.795 - 1.151| = |-0.356|$

$E_6 = 0.356$

Comparando con el valor de $E_6$ con el valor de la tolerancia

$0.356 > 0.001$

La séptima iteración (con $x_6 = 0.795$ ) es

$x_7 = q(x_7 ) = q(0.795)$

$x_7 = \sqrt{\frac{e^{0.795}}{5}}$

$x_7 = 0.665$

El séptimo error es

$E_7 = |x_7 - x_6 |$

$E_7 = |0.665 - 0.795| = |-0.13|$

$E_7 = 0.13$

Comparando con el valor de $E_7$ con el valor de la tolerancia

$0.13 > 0.001$

La octava iteración (con $x_7 = 0.665$ ) es

$\displaystyle x_8 = q(x_8 ) = q(0.665)$

$\displaystyle x_8 = \sqrt{\frac{e^{0.665}}{5}}$

$x_8 = 0.624$

El octavo error es

$E_8 = |x_8 - x_7 |$

$E_8 = |0.624 - 0.665|=|-0.031|$

$E_8 = 0.031$

Comparando con el valor de $E_8$ con el valor de la tolerancia

$E_8 > \text{Tolerancia}$

La novena iteración (con $x_8 = 0.624$ ) es

$\displaystyle x_9 = q(x_8 ) = q(0.624)$

$\displaystyle x_9 = \sqrt{\frac{e^{0.624}}{5}}$

$x_9 = 0.611$

El noveno error es

$E_9 = |x_9 - x_8 |$

$E_9 = |0.611 - 0.624|=|-0.013|$

$E_9 = 0.013$

Comparando con el valor de $E_9$ con el valor de la tolerancia

$0.013 > 0.01$

La décima iteración (con $x_9 = 0.611$ ) es

$\displaystyle x_{10} = q(x_9 ) = q(0.611)$

$\displaystyle x_{10} = \sqrt{\frac{e^{0.611}}{5}}$

$x_{10} = 0.607$

El décimo error es

$E_{10} = |x_{10} - x_9 |$

$E_{10} = |0.607 - 0.611|=|-0.004|$

$E_{10} = 0.004$

Comparando con el valor de $E_{10}$ con el valor de la tolerancia

$0.004 > 0.001$

La undécima iteración (con $x_{10} = 0.607$ ) es

$\displaystyle x_{11} = q(x_{10}) = q(0.607)$

$\displaystyle x_{11} = \sqrt{\frac{e^{0.607}}{5}}$

$x_{11} = 0.605$

El undécimo error es

$E_{11} = |x_{11} - x_{10}|$

$E_{11} = |0.605 - 0.607|=|-0.002|$

$E_{11} = 0.002$

Comparando con el valor de $E_{11}$ con el valor de la tolerancia

$0.002 > 0.001$

La duodécima iteración (con $x_{11} = 0.605$ ) es

$\displaystyle x_{12} = q(x_{11}) = q(0.605)$

$\displaystyle x_{12} = \sqrt{\frac{e^{0.605}}{5}}$

$x_{12} = 0.605$

El duodécima error es

$E_{12} = |x_{12} - x_{11}|$

$E_{12} = |0.605 - 0.605| = |0|$

$E_{12} = 0$

Comparando con el valor de $E_{12}$ con el valor de la tolerancia

$0 < 0.001$

Este último error ya es menor que la tolerancia, por lo tanto, el último valor de x (es decir, $x_{11}$ ) es el resultado final. Entonces

$\therefore x = 0.605$

Problema 3. Encontrar la raíz negativa para $x^3 - 2x + 5 = 0$ con tolerancia de $1 \times {10}^{-2}$ .

Solución. Se elabora una tabulación tomando sólo los valores negativos de «x» desde $x=-4$ hasta $x=0$ .

Existe un cambio de signo, entre $x=-3$ y $x=-2$ . El valor de $x_0$ es

$\displaystyle x_0 = \frac{b+a}{2}$

$\displaystyle x_0 = - \frac{5}{2}$

$x_0 = -2.5$

De la función dada por el problema, se despeja una variable «x» y se coloca en el primer miembro mientras que lo restante se posiciona en el segundo miembro

$x^3 - 2x + 5 = 0$

$x^3 = 2x - 5$

$\displaystyle x = \sqrt[3]{2x-5}$

$\displaystyle q(x) = \sqrt[3]{2x-5}$

La primera iteración (con $x_0 = -2.5$ ) es

$\displaystyle x_1 = q(x_0 ) = q(-2.5)$

$\displaystyle x_1 = \sqrt[3]{2(-2.5)-5}$

$x_1 = -2.154$

El primer error es

$E_1 = |x_1 - x_0 |$

$E_1 = |(-2.154) - (-2.5)| = |-2.154+2.5| = |0.346|$

$E_1 = 0.346$

Comparando con el valor de $E_1$ con el valor de la tolerancia

$0.346 > 0.01$

Este error es mayor que la tolerancia, por lo que, se pasa a la segunda iteración (con $x_1 = -2.154$ ), y es

$\displaystyle x_2 = q(x_1 ) = q(-2.154)$

$\displaystyle x_2 = \sqrt[3]{2(-2.154)-5}$

$x_2 = -2.104$

El segundo error es

$E_2 = |x_2 - x_1 |$

$E_2 = |(-2.104) - (-2.154)| = |-2.104+2.154| = |0.05|$

$E_2 = 0.05$

Comparando con el valor de $E_2$ con el valor de la tolerancia

$0.05 > 0.01$

La tercera iteración (con $x_2 = -2.104$ ) es

$\displaystyle x_3 = q(x_2 ) = q(-2.104)$

$\displaystyle x_3 = \sqrt[2]{2(-2.104)-5}$

$x_3 = -2.096$

El tercer error es

$E_3 = |x_3 - x_2 |$

$E_3 = |(-2.096) - (-2.104)|=|-2.096+2.104|=|0.008|$

$E_3 = 0.008$

Comparando con el valor de $E_3$ con el valor de la tolerancia

$0.008 < 0.01$

Este error ya es menor que la tolerancia, por lo tanto, el último valor de «x» calculado es el resultado final. Por lo tanto

$\therefore x = -2.096$

Problema 4. Encontrar la raíz positiva para $2x^2 - x - 4 = 0$ con tolerancia de $1 \times {10}^{-2} = 0.01$ .

Solución. Se lleva a cabo una tabulación tomando sólo los valores positivos de «x», comenzando desde $x=0$ hasta $x=3$ .

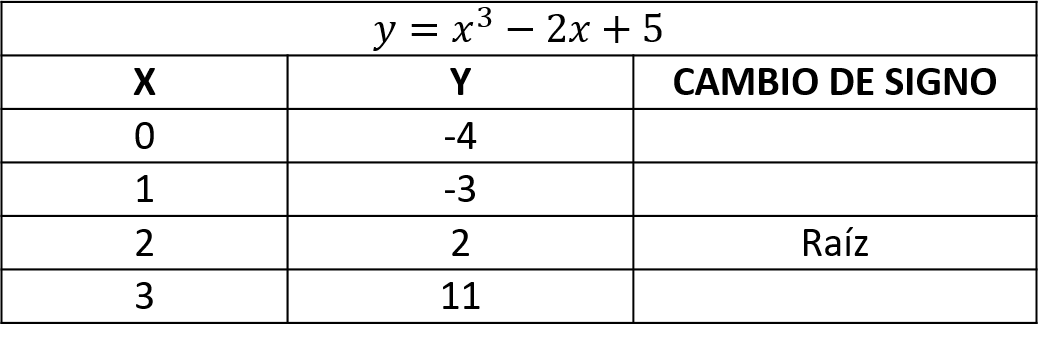
En la tabulación se presentan un sólo cambio de signo (raíz), entre $x=1$ y $x=2$ . El valor de $x_0$ es

$\displaystyle x_0 = \frac{b+a}{2}$

$\displaystyle x_0 = \frac{2+1}{2} = \frac{3}{2}$

$x_0 = 1.5$

De la función brindada por el problema se despeja solo una variable «x» (variable independiente) y se coloca en el primer miembro mientras que lo restante se ubicará en el segundo miembro

$2x^2 - x - 4 = 0$

$\displaystyle x^2 = \frac{(x+4}{2}$