Método de Newton – Raphson. Segundo método abierto. Métodos numéricos.

Introducción

Dada una función $f(x)$ que se representa en el plano $xy$ mostrado en la figura 1.

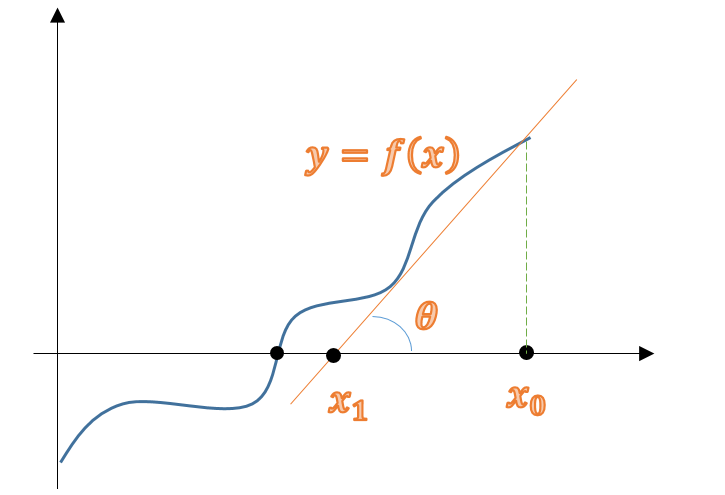
Imagen1 — *Figura 1. Representación gráfica de una función dada para el método de Newton – Raphson.*

El resultado de una derivada pertenece a un ángulo tangente

$\tan{\theta} = {f}^{'} (x_0 )$

Por la función trigonométrica de la tangente

$\displaystyle {f}^{'} (x_0 ) = \frac{f(x_0 )}{x_0-x_1}$

Despejando $x_0 - x_1$

$\displaystyle x_0 - x_1 = \frac{f(x_0 )}{{f}^{'} (x_0 )}$

Y despejando $x_1$

$\displaystyle -x_1 = \frac{f(x_0 )}{f^{'} (x_0 )} - x_0$

$\displaystyle x_1 = x_0 - \frac{f(x_0 )}{f^{'} (x_0 )}$

La cual solo es para la primera iteración. Para más iteraciones

$\displaystyle \therefore x_{n+1} = x_n - \frac{f(x_n )}{f^{'} (x_n )}$

donde $n = 0, 1, 2, ...$ .

Y el error es

$E_{n+1} = |x_{n+1} - x_n |$

Imagen2 — *Figura 2. Triángulo rectángulo.*

Problemas resueltos

Problema 1. Sea $x^2 - 2x - 7 = 0$ , encontrar raíz negativa con tolerancia de $1 \times {10}^{-3} = 0.001$ .

Solución. Por medio de la función se lleva a cabo una tabulación donde los valores de «x» son negativos comenzando desde $x=0$ hasta el valor de $x=-3$ .

Existe un cambio de signo, entre $x=-2$ y $x=-1$ . El valor de $x_0$ es

$\displaystyle x_0 = \frac{b+a}{2}$

$\displaystyle x_0= \frac{-2-1}{2} = -\frac{3}{2}$

$x_0 = -1.5$

Para la función dada por el problema, se calcula su primera derivada con respecto a la variable independiente

$f(x) = x^2 - 2x - 7$

$f^{'} (x) = 2x - 2$

Luego, la primera iteración (con $x_0 = -1.5$ ) es

$\displaystyle x_1 = x_0 - \frac{f(x_0 )}{f^{'} (x_0 )}$

$\displaystyle x_1 = -1.5 - \frac{f(-1.5)}{f^{'} (-1.5)}$

$\displaystyle x_1 = - 1.5 - \frac{(-1.5)^2-2(-1.5)-7}{2(-1.5)-2}$

$\displaystyle x_1 = -1.5 - \frac{(-1.75)}{(-5)}$

$x_1 = -1.5 - 0.35$

$x_1 = -1.85$

El primer error es

$E_1 = |x_1 - x_0 |$

$E_1 = |(-1.85) - (-1.5)| = |-1.85+1.5| = |-0.35|$

$E_1 = 0.35$

Comparando el valor de $E_1$ con el valor de la tolerancia

$0.35 > 0.001$

Este error es mayor que la tolerancia, por lo que, se pasa a la segunda iteración (con $x_1 = -1.85$ ), y es

$\displaystyle x_2 = x_1 - \frac{f(x_1 )}{f^{'} (x_1 )}$

$\displaystyle x_2 = -1.85 - \frac{f(-1.85)}{f^{'} (-1.85)}$

$\displaystyle x_2 = -1.85 - \frac{(-1.85)^2-2(-1.85)-7}{2(-1.85)-2}$

$\displaystyle x_2 = -1.85 - \frac{(0.123)}{(-5.7)}$

$x_2 = -1.85+0.022$

$x_2 = -1.828$

El segundo error es

$E_2=|x_2-x_1 |$

$E_2 = |(-1.872)-(-1.85)| =|-1.872+1.85| = |-0.022|$

$E_2 =0.022$

Comparando el valor de $E_2$ con el valor de la tolerancia

$0.022 > 0.001$

Este error es mayor que la tolerancia, por lo que, se pasa a la tercera iteración (con $x_2 = -1.872$ ), y es

$\displaystyle x_3 = x_2 - \frac{f(x_2 )}{f^{'} (x_2 )}$

$\displaystyle x_3=-1.828 - \frac{f(-1.828)}{f^{'} (-1.828)}$

$\displaystyle x_3 = -1.828 - \frac{(-1.828)^2-2(-1.828)-7}{2(-1.828)-2}$

$\displaystyle x_3 = -1.828 - \frac{(-0.002)}{(-5.656)}$

$x_3 = -1.828 - 0.000$

$x_3 = -1.828$

El tercer error es

$E_3 = |x_3 - x_2 |$

$E_3 = |(-1.828) - (-1.828)|$

$E_3 = |-1.828+1.828|$

$E_3 = 0$

Comparando el valor de $E_3$ con el valor de la tolerancia

$0 < 0.001$

Este error ya es menor que la tolerancia, por lo tanto, el último valor de «x» calculado es el valor esperado. Finalmente, el resultado final es

$\therefore x = -1.828$

Problema 2. Sea $\displaystyle x \sin{x} - \frac{3}{4} x = 0$ , encontrar raíz positiva con tolerancia de $1 \times {10}^{-4} = 0.0001$ .

Solución. Se lleva a cabo una tabulación tomando solo los valores positivo de $x$ comenzando con $x=0$ hasta $x=3$ .

Existe un cambio de signo, cuando $x=2$ y $x=3$ . El valor de $x_0$ es

$\displaystyle x_0 = \frac{b+a}{2}$

$\displaystyle x_0 = \frac{3+2}{2} = \frac{5}{2}$

$x_0 = 2.5$

De la función dada por el problema, se deriva una vez con respecto a la variable independiente

$\displaystyle f(x) = x \sin{x} - \frac{3}{4} x = x \sin{x} - 0.75x$

$\displaystyle f^{'} (x) = \sin{x} - x \cos{x} - 0.75$

La primera iteración (con $x_0 = 2.5$ ) es

$\displaystyle x_1 = x_0 - \frac{f(x_0 )}{f^{'} (x_0 )}$

$\displaystyle x_1 = 2.5 - \frac{f(2.5)}{f^{'} (2.5)}$

$\displaystyle x_1 =2.5 - \frac{(2.5)(\sin{2.5}) - (0.75)(2.5)}{\sin{2.5}-(2.5)(\cos{2.5})-0.75}$

$\displaystyle x_1 =2.5 - \frac{(-0.3788)}{(-2.1544)} = 2.5 - 0.1758$

$x_1 = 2.3242$

El primer error es

$E_1 = |x_1 - x_0 |$

$E_1 = |2.3242-2.5|=|-0.1758|$

$E_1 = 0.1758$

Comparando el valor de $E_1$ con el valor de la tolerancia

$0.1758 > 0.0001$

Este error es mayor que la tolerancia, por lo que, se pasa a la segunda iteración (con $x_1 = 2.3242$ ), y es

Para la segunda iteración.

$\displaystyle x_2 = x_1 - \frac{f(x_1 )}{f^{'} (x_1 )}$

$\displaystyle x_2 = 2.3242 - \frac{f(2.3242)}{f^{'} (2.3242)}$

$\displaystyle x_2 = 2.3242 - \frac{(2.3242)(\sin{2.3242})-(0.75)(2.3242)}{\sin{2.3242} - (2.3242)(\cos{2.3242}) - 0.75}$

$\displaystyle x_2 = 2.3242 - \frac{(-0.048)}{(-1.6107)} = 2.3242-0.0298$

$x_2 = 2.2944$

El segundo error es

$E_2 = |x_2-x_1 |$

$E_2 = |2.2944-2.3242|=|0.0298|$

$E_2 = 0.0298$

Comparando el valor de $E_2$ con el valor de la tolerancia

$0.0298 > 0.0001$

Este error es mayor que la tolerancia, por lo que, se pasa a la tercera iteración (con $x_2 = 2.2944$ ), y es

$\displaystyle x_3 = x_2 - \frac{f(x_2 )}{f^{'} (x_2 )}$

$\displaystyle x_3 = 2.2944 - \frac{f(2.2944)}{f^{'} (2.29.44)}$

$\displaystyle x_3 = 2.2944 - \frac{(2.2944)(\sin{2.2944}) - (0.75)(2.2944)}{(sin{2.2944} - (2.2944)(\cos{2.2944}) - 0.75}$

$\displaystyle x_3 = 2.2944 - \frac{(-0.0013)}{(-1.5197)} = 2.2944 - 0.0009$

$x_3 = 2.2935$

El tercer error es

$E_3 = |x_3 - x_2 |$

$E_3 = |2.2935-2.2944|=|0.0009|$

$E_3 = 0.0009$

Comparando el valor de $E_3$ con el valor de la tolerancia

$0.009 > 0.0001$

Este error es mayor que la tolerancia, por lo que, se pasa a la cuarta iteración (con $x_3 = 2.2935$ ), y es

$\displaystyle x_4 = x_3 - \frac{f(x_3 )}{f^{'} (x_3 )}$

$\displaystyle x_4 = 2.2935 - \frac{f(2.2935)}{f^{'} (2.2935)}$

$\displaystyle x_4 = 2.2935 - \frac{(2.2935)(\sin{2.2935})-(0.75)(2.2935)}{\sin{2.2935} - (2.2935)(\cos{2.2935}) - 0.75}$

$\displaystyle x_4 = 2.2935 - \frac{(-0.0001)}{(-1.5169)} = 2.2935 - 0.0001$

$x_4 = 2.2934$

El cuarto error es

$E_4 = |x_4 - x_3 |$

$E_4 = |2.2934 - 2.2935|=|-0.0001|$

$E_4 = 0.0001$

Comparando el valor de $E_4$ con el valor de la tolerancia

$0.0001 = 0.0001$

Como el valor del error ya es igual que la tolerancia, el último valor de «x» es el resultado final.

$\therefore x = 2.2934$

Problema 3. Sea $e^{2x} - x^2 = 0$ , encontrar raíz negativa con tolerancia de $1 \times {10}^{-3} = 0.001$ .

Solución. Se lleva a cabo una tabulación tomando los valores de «x» negativos comenzando con $x=0$ hasta $x=-3$ .

En la tabulación, la función presenta un cambio de signo cuando $x=0$ y $x=-1$ . El valor de $x=0$ es

$\displaystyle x_0 = \frac{b+a}{2}$

$\displaystyle x_0 = \frac{-1+0}{2} = -\frac{1}{2}$

$x_0 = -0.5$

De la función dada por el problema, se deriva una vez con respecto a la variable independiente

$f(x) = e^{2x} - x^2$

$f^{'} (x) = 2e^{2x} - 2x$

La primera iteración (con $x_0 = -0.5$ ) es

$\displaystyle x_1 = x_0 - \frac{f(x_0 )}{f^{'} (x_0 )}$

$\displaystyle x_1 = -0.5 - \frac{f(-0.5)}{f^{'} (-0.5)}$

$\displaystyle x_1 = -0.5 - \frac{e^{2(-0.5)} -(-0.5)^2}{2e^{2(-0.5)} -2(-0.5)}$

$\displaystyle x_1 = -0.5 - \frac{(0.1179)}{(1.7358)}= -0.5-0.0679$

$x_1 = -0.5679$

El primer error es

$E_1 = |x_1 - x_0 |$

$E_1 = |(-0.5679)-(-0.5)| =|-0.5679+0.5|=|-0.0679|$

$E_1 = 0.0679$

Comparando con el valor de $E_1$ con el valor de la tolerancia

$0.0679 > 0.001$

Este error es mayor que la tolerancia, por lo que, se pasa a la segunda iteración (con $x_1 = -0.5679$ ), y es

$\displaystyle x_2 = x_1 - \frac{f(x_1 )}{f^{'} (x_1 )}$

$\displaystyle x_2 = -0.5679 - \frac{f(-0.5679)}{f^{'} (-0.5679)}$

$\displaystyle x_2 = - 0.5679 - \frac{e^{2(-0.5679)} - (-0.5679)^2}{2e^{2(-0.5679)} - 2(-0.5679)}$

$\displaystyle x_2 = -0.5679 - \frac{(-0.0013)}{(1.7781)} = -0.5679 - 0.0007$

$x_2 = -0.5672$

El segundo error es

$E_2 = |x_1-x_0 |$

$E_2 = |(-0.5672)-(-0.5679)| = |-0.5672+0.5679|=|0.0007|$

$E_2 = 0.0007$

Comparando con el valor de $E_2$ con el valor de la tolerancia

$0.0007 > 0.001$

El resultado final es

$\therefore x_2 = -0.5672$

Método de Newton – Raphson. Segundo método abierto. Métodos numéricos.

Introducción

Problemas resueltos

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta

Método de Newton – Raphson. Segundo método abierto. Métodos numéricos.

Introducción

Problemas resueltos

Comparte esto:

Relacionado

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta