Método de la regla falsa. Primer método cerrado. Métodos numéricos.

Introducción

Sea $f(x)$ una función donde presenta dos valores: valor inferior y valor superior, representados en una gráfica en el plano.

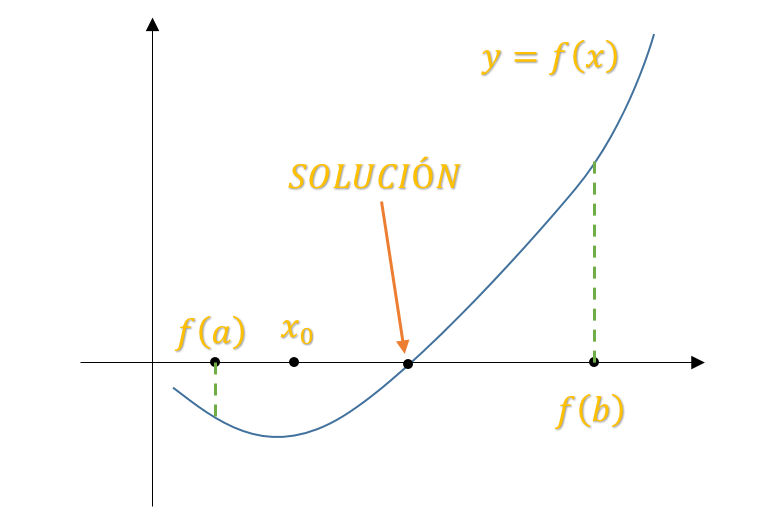
Imagen1 — *Figura 1. Representación gráfica de una función en el plano.*

Esto genera dos triángulos rectángulos y se puede analizar por semejanza de triángulos.

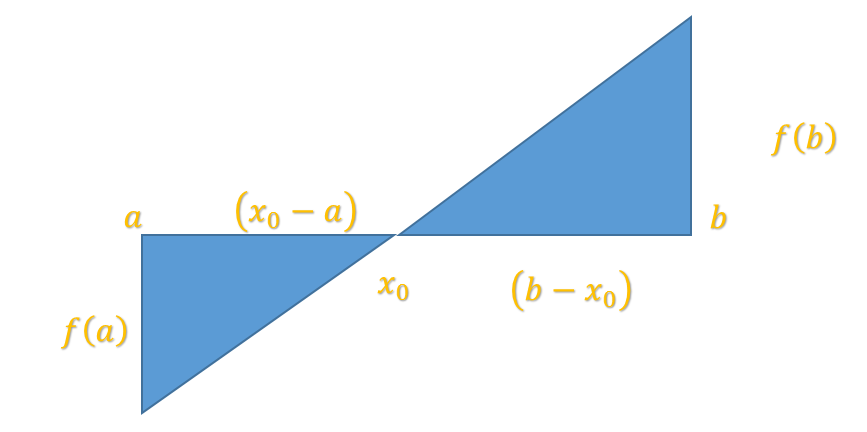
Imagen2 — *Figura 2. Análisis por triángulos semejantes*

Por triángulos semejantes, se despeja $x_0$

$\displaystyle \frac{f(b)}{b-x_0} = \frac{-f(a)}{x_0-a}$

$(x_0 - a)f(b) = -(b - x_0 )f(a)$

$x_0 f(b) - af(b) = -bf(a) + x_0 f(a)$

$x_0 f(b) - x_0 f(a) = -bf(a) + af(b)$

$x_0 [f(b) - f(a)] = af(b) - bf(a)$

$\displaystyle x_0 = \frac{af(b)-bf(a)}{f(b)-f(a)}$

La cual, esta fórmula sólo es para calcular el valor de x en la primera iteración. Para más iteraciones

$\displaystyle x_{n+1} = \frac{x_n f(k)-kf(x_n )}{f(k)-f(x_n ) }$

Donde

$k$ representa los valores que tomará de a o de b.
$f(x_0 )$ si esto es signo contrario de f(a) y f(b).

Para calcular el error

$E_{n+1} =|x_{n+1} - x_n |$

Problemas resueltos

Problema 1. Obtener raíz positiva de $x^2 - 2x - 8 = 0$ con tolerancia de $1 \times {10}^{-2} = 0.01$ .

Solución. Se elabora una tabulación tomando los valores de «x» positivos desde $x=0$ hasta $x=4$ .

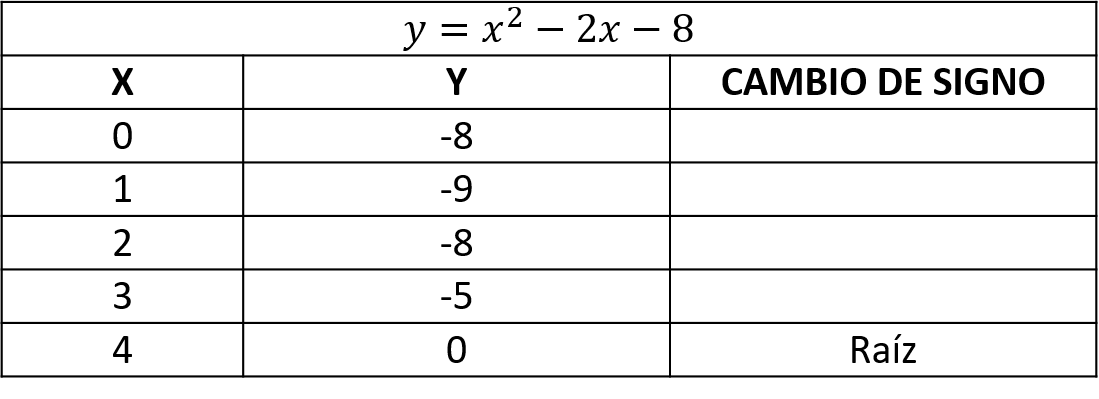
En la tabulación, la función presenta un cambio de signo entre $x=3$ y $x=4$ , por lo que, los valores de a y b son 3 y 4.

De $f(x) = x^2 - 2x - 8$ se evalúan los valores de a y b en esa función

Para obtener $x_0$ , se toma la fórmula de la regla falsa y se sustituyen los datos

$\displaystyle x_0 = \frac{af(b)-bf(a)}{f(b)-f(a)}$

$\displaystyle x_0 = \frac{(3)f(4)-(4)f(3)}{f(4)-f(3)}$

$\displaystyle x_0 = \frac{(-5)(0)-(4)(-5)}{0-(-5)}$

$\displaystyle x_0 = \frac{20}{5}$

$x_0 = 4$

Sustituyendo este resultado en la función del problema

$f(x_0 ) = f(4) = (4)^2 - 2(4) - 8$

$f(4) = 0$

Este resultado se considera positivo, sin embargo, para poder tomar el valor de $k$ debe brindar un valor numérico con signo opuesto al momento de evaluar la función $f(x)$ , por lo tanto, en vez de utilizar el valor de $b$ donde $f(b)$ da un valor numérico positivo, se utilizará el valor de $a$ donde $f(a)$ da un valor numérico negativo, y esto lleva a que el pivote es $k = a = 3$ .

Utilizando la fórmula de la regla falsa para obtener la primera iteración

$\displaystyle x_1 = \frac{x_0 f(k)-kf(x_0 )}{f(k)-f(x_0 )}$

$\displaystyle x_1 = \frac{(4)f(3)-3f(4)}{f(3)-f(4)}$

$\displaystyle x_1 = \frac{4(-5)-3(0)}{-5-0}$

$\displaystyle x_1 = \frac{(-20)}{(-5)}$

$x_1 = 4$

Calculando el primer error

$E_1 = |x_1 - x_0 |$

$E_1 = |4-4|$

$E_1 = 0$

Comparando el valor de $E_1$ con el valor de la tolerancia

$0 < 0.01$

Se observa que este error ya es menor que la tolerancia, por lo que, el último valor de «x» calculado es el indicado. Finalmente

$\therefore x = 4$

Problema 2. Obtener raíz positiva de $x^2 + x - 10 = 0$ con tolerancia de $1 \times {10}^{-2} = 0.01$

Solución. Se lleva a cabo una tabulación con solo valores de «x» positivos, comenzando desde $x=0$ hasta $x=3$ .

En la tabulación, la función presenta un cambio de signo (raíz), entre $x=2$ y $x=3$ . Entonces, el valor de a será $a=2$ y el valor de b será $b=3$ .

De la función dada, se evalúa, primero con el valor de «a» y después con el valor de «b».

$f(x) = x^2 + x - 10$

Por medio de la fórmula de la regla falsa, se calcula $x_0$

$\displaystyle x_0 = \frac{af(b)-bf(a)}{f(b)-f(a)}$

$\displaystyle x_0 = \frac{(2)f(3)-(3)f(2)}{f(3)-f(2)}$

$\displaystyle x_0 = \frac{(2)(2)-(3)(-4)}{2-(-4)}$

$\displaystyle x_0 = \frac{4+12}{2+4}$

$\displaystyle x_0 = \frac{16}{6}$

$\displaystyle x_0 = 2.667$

Sustituyendo el valor de $x_0$ en la función del problema

$f(x_0 ) = f(2.667) = (2.667)^2+(2.667)-10$

$f(x_0 ) = -0.222$

Este resultado es negativo, sin embargo, para poder tomar el valor de $k$ debe brindar un valor numérico con signo opuesto al momento de evaluar la función $f(x)$ , por lo tanto, en vez de utilizar el valor de $a$ donde $f(a)$ da un valor numérico negativo, se utilizará el valor de $b$ donde $f(b)$ da un valor numérico positivo, y esto lleva a que el pivote es $k = b = 3$ .

Utilizando la fórmula de la regla falsa para obtener la primera iteración

$\displaystyle x_1 = \frac{x_0 f(k)-kf(x_0 )}{f(k)-f(x_0 )}$

$\displaystyle x_1 = \frac{(2.667)f(3)-3f(2.667)}{f(3)-f(2.667)}$

$\displaystyle x_1 = \frac{2.667(2)-3(-0.222)}{2-(-0.222)}$

$\displaystyle x_1 = \frac{5.334+0.666}{2+0.222}$

$\displaystyle x_1 = \frac{6}{2.222}$

$x_1 = 2.7$

El valor del primer error es

$E_1 = |x_1 - x_0 |$

$E_1 = |2.7 - 2.667|=|0.033|$

$E_1 = 0.033$

Comparando el valor de $E_1$ con el valor de la tolerancia

$0.033 > 0.01$

Se dice que el error es mayor que la tolerancia, por lo que, se continua con la siguiente iteración. Evaluando el la función del problema con el valor de $x_1 = 2.7$

$f(x_1 ) = f(2.7) = (2.7)^2 + (2.7) - 10$

$f(x_1 ) = -0.010$

La segunda iteración es

$\displaystyle x_2 = \frac{x_2 f(k)-kf(x_2 )}{f(k)-f(x_2 )}$

$\displaystyle x_2 = \frac{(2.7)f(3)-3f(2.7)}{f(3)-f(2.7)}$

$\displaystyle x_2 = \frac{2.7(2)-3(-0.010)}{2-(-0.010)}$

$\displaystyle x_2 = \frac{5.4+0.030}{2+0.010}$

$\displaystyle x_2 = \frac{5.43}{2.01}$

$x_2 = 2.701$

Calculando el segundo error

$E_2 = |x_2 - x_1 |$

$E_2 = |2.701-2.7|=|0.001|$

$E_2 = 0.001$

Comparando el valor de $E_2$ con el valor de la tolerancia

$0.001 < 0.01$

El valor de este error ya es menor que la tolerancia, por lo tanto, el último valor de «x» calculado es el valor indicado. Finalmente

$\therefore x = 2.701$

Problema 3. Obtener raíz positiva de $\sin{2x} + x - 1 = 0$ con tolerancia de $1 \times {10}^{-2} = 0.01$ .

Solución. Se elabora una tabulación tomando la función del problema y los valores de «x» positivos, comenzando desde $x=0$ hasta $x=2$ .

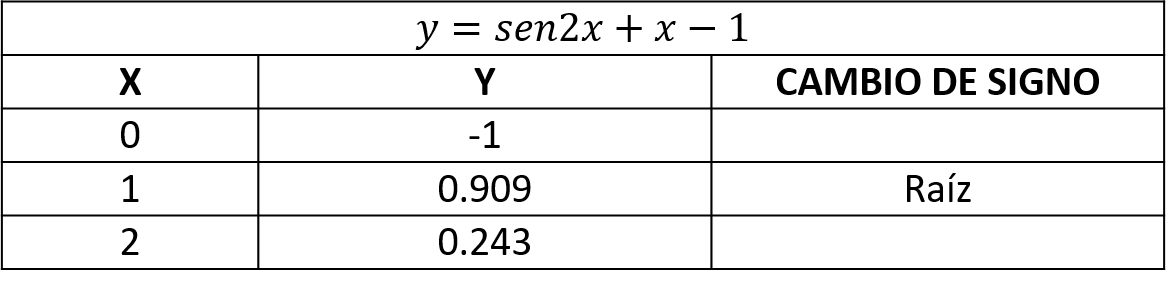
En la tabulación, la función presenta un cambio de signo (raíz), entre $x=0$ y $x=1$ , por lo que, los valores a tomar son $a=0$ y $b=1$ .

De la función del problema, se evalúa primero con el valor de $a$ y luego con el valor de $b$ .

$f(x) = \sin{2x} + x - 1$

$f(a) = f(0) = \sin{[2(0)]} + 0 - 1 = -1$

$f(b) = f(1) = \sin{[2(1)]} + 0 - 1 = 0.909$

Se calcula el valor de $x_0$ utilizando la fórmula de la regla falsa

$\displaystyle x_0 = \frac{af(b)-bf(a)}{f(b)-f(a)}$

$\displaystyle x_0 = \frac{(0)f(1)-(1)f(0)}{f(1)-f(0)}$

$\displaystyle x_0 = \frac{0(0.909)-(1)(-1)}{0.909-(-1)}$

$\displaystyle x_0 = \frac{0+1}{0.909+1}$

$\displaystyle x_0 = \frac{1}{1.909}$

$\displaystyle x_0 = 0.524$

Con este valor de $x_0$ se sustituye en la función dada por el problema

$f(x_0 ) = f(0.524) = \sin{(2 \cdot 0.524)} + 0.524 - 1$

$f(x_0 ) = 0.390$

Este resultado es positivo, sin embargo, para poder tomar el valor de $k$ debe brindar un valor numérico con signo opuesto al momento de evaluar la función $f(x)$ , por lo tanto, en vez de utilizar el valor de $b$ donde $f(b)$ da un valor numérico positivo, se utilizará el valor de $a$ donde $f(a)$ da un valor numérico negativo, y esto lleva a que el pivote es $k = a = 0$ .

La primera iteración es

$\displaystyle x_1 = \frac{x_0 f(k)-kf(x_0 )}{f(k)-f(x_0 )}$

$\displaystyle x_1 = \frac{(0.524)f(0)-(0)f(0.524)}{f(0)-f(0.524)}$

$\displaystyle x_1 = \frac{0.524(-1)-(0)(0.390)}{-1-0.390}$

$\displaystyle x_1 = \frac{-0.524+0}{-1-0.390}$

$\displaystyle x_1 = \frac{(-0.524)}{(-1.390)}$

$\displaystyle x_1 = 0.377$

El valor del primer error es

$E_1 = |x_1 - x_0 |$

$E_1 = |0.377-0.524|=|-0.147|$

$E_1 = 0.147$

Comparando con el valor de $E_1$ con el valor de la tolerancia

$0.147 > 0.01$

Este valor del error es mayor que la tolerancia, por lo que, se pasa a la siguiente iteración. Tomando el valor de $x_1$ y evaluándolo en la función del problema