Introducción
El polinomio de Lagrange es el siguiente
Donde
Si el problema o enunciado muestra sólo dos nodos, los parámetros a calcular son los siguientes
Y el polinomio interpolante esperado es
Si el problema o enunciado muestra sólo tres nodos, los parámetro a calcular son los siguientes
Y el polinomio interpolante esperado es
Si se desea saber que tan cerca es el valor evaluado en un polinomio interpolante (valor aproximado calculado con respecto a la función del problema (valor exacto) solo basta con determinar el error. Su fórmula es la siguiente
Donde
representa el error.
representa el valor exacto (función evaluada brindada por el problema).
representa el valor aproximado (polinomio evaluado calculado).
Problema resuelto
Problema 1. Sea con nodos
, usar el polinomio de Lagrange para hallar
y evaluar
(interpolar).
Solución. De los nodos brindados por el problema, se evalúan cada uno en la función .
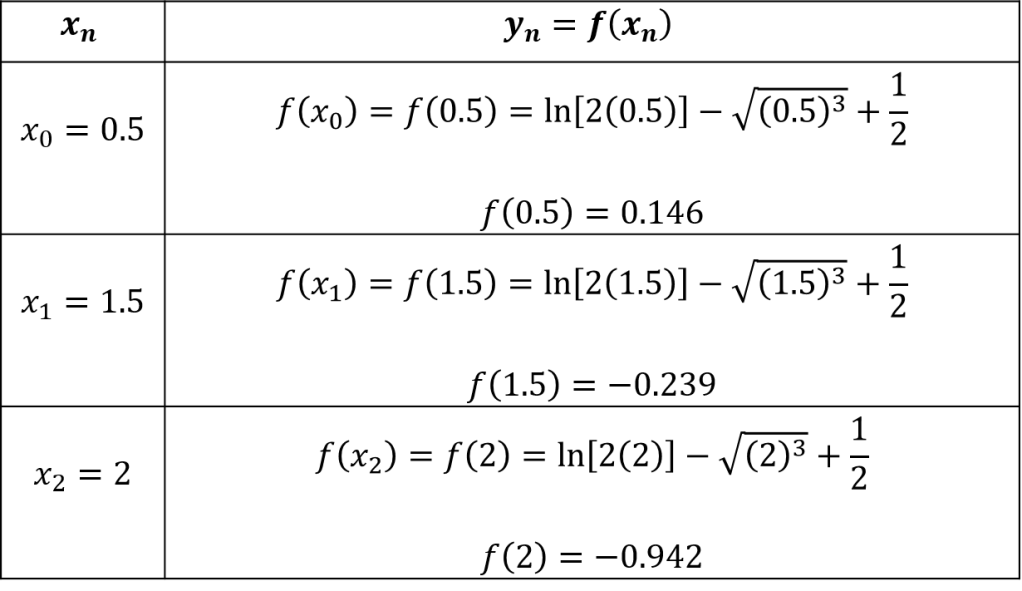
Calculando
Calculando
Calculando
Utilizando la fórmula del polinomio de Lagrange
Sustituyendo
Por lo tanto
Interpolando la función cuando (obtenido de
)
Antes de calcular el error, se evalúa la función del problema cuando
El valor del error
Esto se refiere a que entre el valor de y el valor de
existe una diferencia del 0.001 unidades.