Introducción
Una ecuación diferencial ordinaria lineal está representado de la siguiente manera
Y debe tener una condición inicial en un intervalo cerrado
. Con el método de Euler, si
y
, la condición inicial también puede escribirse de la siguiente manera
; remplazando
por
, el primer dato que toma este método es el siguiente
Con .
La fórmula general del método de Euler es
Donde
y
representan los valores de
y
por medio de
.
es el tamaño de paso y se calcula por la fórmula
es el valor inferior del intervalo cerrado
es el valor superior del intervalo cerrado
es el tamaño o las iteraciones a considerar (
)
es el valor de la abscisa anterior calculado basado en
, que es la variable a calcular y su fórmula es
Problema resuelto
Problema 1. Encontrar ,
para
, con valor inicial de
y con
.
Solución. En la ecuación diferencial, se observa que
Al analizar la condición inicial , se observa que
y
. El valor de
es
Por medio de la fórmula , se muestra los siguientes valores

Por el método de Euler
La primera iteración es (con )
La segunda iteración es (con )
La tercera iteración (con ) es
)
La cuarta iteración (con ) es
Finalmente, en un resumen se visualizan estos resultados aplicados por el método de Euler

Ahora, antes de calcular los valores exactos, primer se resuelve la ecuación diferencial aplicando el método de separación de variables.
Esta expresión es la solución general de la ecuación diferencial del problema. Obteniendo el valor de por medio del punto inicial
Entonces
Este resultado es la solución particular de la ecuación diferencial del problema. Tomando los valores de (desde
hasta
), se evalúan en la función
, obtenida de la ecuación diferencial; los resultados se muestran en la siguiente tabla
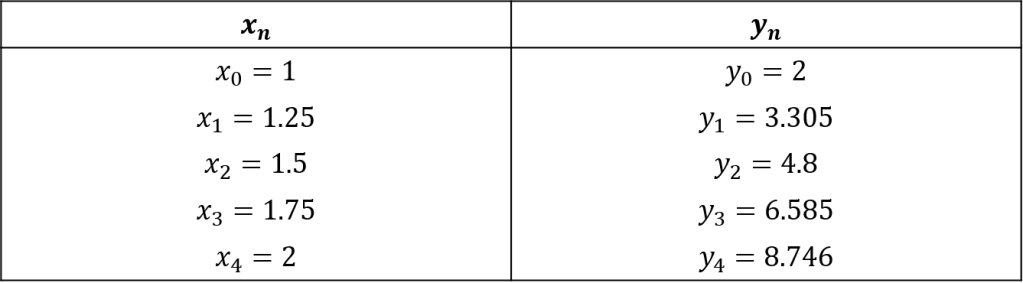
Al graficar los puntos calculados por el método de Euler (valores aproximados) y por evaluación directa (valores exactos), se tiene lo siguiente


