Solución de ecuaciones diferenciales lineales de primer orden utilizando el método de Heun. Métodos numéricos.

Introducción

Este método también es llamado como el método de Euler mejorado, y su fórmula es la siguiente

$\displaystyle y_{n+1} = y_n + \frac{h}{2} [f(x_n,y_n ) + f(x_{n+1},y_n ) + h \cdot f(x_n,y_n )]$

En la primera iteración $y_1 = y_0 + f(x_0, y_0 )$ predice un valor de $y(x_1 )$ , y

$\displaystyle y_1 + y_0 + \frac{h}{2} [f(x_0,y_0 ) + f(x_1,y_0 ) + h \cdot f(x_0,y_0 )]$

corrige la estimación anterior.

Problema resuelto

Problema 1. Dada la siguiente ecuación diferencial $y^{'} = x - y + 1$ para $y(0) = 1$ en $0 \le x \le 1$ , utilizar el método de Heun para obtener una aproximación de la solución hasta $n=10$ .

Solución. De la ecuación diferencial, sea $f(x,y) = x - y + 1$ , donde $f(x_n,y_n ) = x_n - y_n + 1$ y, $x_0 = 0$ y $y_0 = 1$ . Del intervalo $0 \le x \le 1$ , los valores de $a$ y $b$ son $0$ y $1$ respectivamente. Calculando $h$

$\displaystyle h = \frac{b-a}{n}$

$h = \frac{1-0}{10} = \frac{1}{10}$

$h=0.1$

Utilizando la fórmula de Heun, se determina, de la primera iteración (con n=0), el valor de $x_1$

$x_1 = x_0 + h$

$x_1 = 0 + 0.1$

$x_1 = 0.1$

Y el valor de $y_1$

$\displaystyle y_1 = y_0 + \frac{h}{2} [f(x_0,y_0 ) + f(x_1,y_0 ) + h \cdot f(x_0,y_0 )]$

$\displaystyle y_1 = 1 + \frac{0.1}{2} [f(0,1)+f(0.1,1)+(0.1)f(0,1)]$

$y_1 = 1+0.05[(0-1+1)+(0.1-1+1)+(0.1)(0-1+1)]$

$y_1=1+(0.05)(0+0.1+0)=1+(0.05)(0.1)$

$y_1=1.005$

En la segunda iteración (con $n=1$ ), el valor de $x_2$ es

$x_2 = x_1+h$

$x_2 =0.1+0.1$

$x_2=0.2$

Y el valor de $y_2$ es

$\displaystyle y_2 = y_1 + \frac{h}{2} [f(x_1,y_1 )+f(x_2,y_1 )+hf(x_1,y_1 )]$

$\displaystyle y_2 = 1.005 + \frac{0.1}{2} [f(0.1,1.005)+f(0.2,1.005)+(0.1) \cdot f(0.1,1.005)]$

$y_2 =1.005+0.05[(0.1-1.005+1)+(0.2-1.005+1)+(0.1)(0.1-1.005+1)]$

$y_2=1.005+(0.05)(0.095+0.195+0.0095)=1.005+(0.05)(0.2995)$

$y_2=1.02$

En la tercera iteración (con $n=2$ ), el valor de $x_3$ es

$x_3 = x_2+h$

$x_3 = 0.2+0.1$

$x_3=0.3$

Y el valor de $y_3$ es

$\displaystyle y_3 = y_2 + \frac{h}{2} [f(x_2,y_2 )+f(x_3,y_2 )+h \cdot f(x_2,y_2 )]$

$\displaystyle y_3 = 1.02 + \frac{0.1}{2} [f(0.2,1.02)+f(0.3,1.02)+(0.1) \cdot f(0.2,1.02)]$

$y_3 = 1.02+0.05[(0.2-1.02+1)+(0.3-1.02+1)+(0.1)(0.2-1.02+1)]$

$y_3 = 1.02+(0.05)(0.18+0.28+0.018)=1.02+(0.05)(0.478)$

$y_3 = 1.0439$

En la cuarta iteración (con $n=3$ ), el valor de $x_4$ es

$x_4 = x_3 + h$

$x_4 = 0.3 + 0.1$

$x_4 = 0.4$

Y el valor de $y_4$ es

$\displaystyle y_4 = y_3 + \frac{h}{2} [f(x_3,y_3 )+f(x_4,y_3 )+h \cdot f(x_3,y_3 )]$

$\displaystyle y_4 = 1.0439 + \frac{0.1}{2} [f(0.3,1.0439)+f(0.4,1.0439)+(0.1) \cdot f(0.3,1.0439)]$

$\displaystyle y_4 = 1.0439 + 0.05[(0.3-1.0439+1)+(0.4-1.0439+1)+(0.1)(0.3-1.0439+1)]$

$y_4 =1.0439+(0.05)(0.2561+0.3561+0.0256)=1.0439+(0.05)(0.6378)$

$y_4=1.0759$

En la quinta iteración (con $n=4$ ), el valor de $x_5$ es

$x_5=x_4+h$

$x_5=0.4+0.1$

$x_4=0.5$

Y el valor de $y_5$ es

$\displaystyle y_5 = y_4 + \frac{h}{2} [f(x_4,y_4 )+f(x_5,y_4 )+h \cdot f(x_4,y_4 )]$

$\displaystyle y_5 = 1.0759 + \frac{0.1}{2} [f(0.4,1.0759)+f(0.5,1.0759)+(0.1) \cdot f(0.4,1.0759)]$

$\displaystyle y_5=1.0759+0.05[(0.4-1.0759+1)+(0.5-1.0759+1)+(0.1)(0.4-1.0759+1)]$

$y_5 = 1.0759+(0.05)(0.3241+0.4241+0.0324)=1.0759+(0.05)(0.7806)$

$y_5=1.1149$

En la sexta iteración (con $n=5$ ), el valor de $x_6$ es

$x_6=x_5+h$

$x_6=0.5+0.1$

$x_6=0.6$

Y el valor de $y_6$ es

$\displaystyle y_6 = y_5 + \frac{h}{2} [f(x_5,y_5 )+f(x_6,y_5 )+h \cdot f(x_5,y_5 )]$

$\displaystyle y_6 = 1.1149 + \frac{0.1}{2} [f(0.5,1.1149)+f(0.6,1.1149)+(0.1) \cdot f(0.5,1.1149)]$

$\displaystyle y_6=1.1149+0.05[(0.5-1.1149+1)+(0.6-1.1149+1)+(0.1) \cdot (0.5-1.1149+1)]$

$y_6=1.1149+(0.05)(0.3851+0.4851+0.0385)=1.1149+(0.05) \cdot (0.9087)$

$y_6=1.1603$

En la séptima iteración (con $n=6$ ), el valor de $x_7$ es

$x_7=x_6+h$

$x_7=0.6+0.1$

$x_7 = 0.7$

Y el valor de $y_7$ es

$\displaystyle y_7 = y_6 + \frac{h}{2} [f(x_6,y_6 )+f(x_7,y_6 )+h \cdot f(x_6,y_6 )]$

$\displaystyle y_7 = 1.1603 + \frac{0.1}{2} [f(0.6,1.1603)+f(0.7,1.1603)+(0.1) \cdot f(0.6,1.1603)]$

$y_7=1.1603+0.05[(0.6-1.1603+1)+(0.7-1.1603+1)+(0.1)(0.6-1.1603+1)]$

$y_7=1.1603+(0.05)(0.4397+0.5397+0.044)=1.1603+(0.05)(1.0234)$

$y_7=1.2115$

En la octava iteración (con $n=7$ ), el valor de $x_8$ es

$x_8=x_7+h$

$x_8=0.7+0.1$

$x_8=0.8$

Y el valor de $y_8$ es

$\displaystyle y_8 = y_7 + \frac{h}{2} [f(x_7,y_7 )+f(x_8,y_7 )+h \cdot f(x_7,y_7 )]$

$\displaystyle y_8 = 1.2115 + \frac{0.1}{2} [f(0.7,1.2115)+f(0.8,1.2115)+(0.1) \cdot f(0.7,1.2115)]$

$y_8=1.2115+0.05[(0.7-1.2115+1)+(0.8-1.2115+1)+(0.1)(0.7-1.2115+1)]$

$y_8=1.2115+(0.05)(0.4885+0.5885+0.0489)=1.2115+(0.05)(1.1259)$

$y_8=1.2678$

En la novena iteración (con $n=8$ ), el valor de $x_9$ es

$x_9=x_8+h$

$x_9=0.8+0.1$

$x_9=0.9$

Y el valor de $y_9$ es

$\displaystyle y_9 = y_8 + \frac{h}{2} [f(x_8,y_8 )+f(x_9,y_8 )+h \cdot f(x_8,y_8 )]$

$\displaystyle y_9 = 1.2678 + \frac{0.1}{2} [f(0.8,1.2678)+f(0.9,1.2678)+(0.1) \cdot f(0.8,1.2678)]$

$y_9=1.2678+0.05[(0.8-1.2678+1)+(0.9-1.2678+1)+(0.1)(0.8-1.2678+1)]$

$y_9=1.2678+(0.05)(0.5322+0.6322+0.0532)=1.2678+(0.05)(1.2176)$

$y_9=1.3287$

En la décima iteración (con $n=9$ ), el valor de $x_10$ es

$x_10=x_9+h=0.9+0.1$

$x_10=1$

Y el valor de $y_{10}$ es

$\displaystyle y_{10} = y_9 + \frac{h}{2} [f(x_9,y_9 )+f(x_10,y_9 )+h \cdot f(x_9,y_9 )]$

$\displaystyle y_{10} = 1.3287 + \frac{0.1}{2} [f(0.9,1.3287)+f(1,1.3287)+(0.1)f(0.9,1.3287)]$

$y_{10} = 1.3287+0.05[(0.9-1.3287+1)+(1-1.3287+1)+(0.1)(0.9-1.3287+1)]$

$y_{10}=1.3287+(0.05)(0.5713+0.6713+0.0571)=1.3287+(0.05)(1.2997)$

$y_{10} = 1.3937$

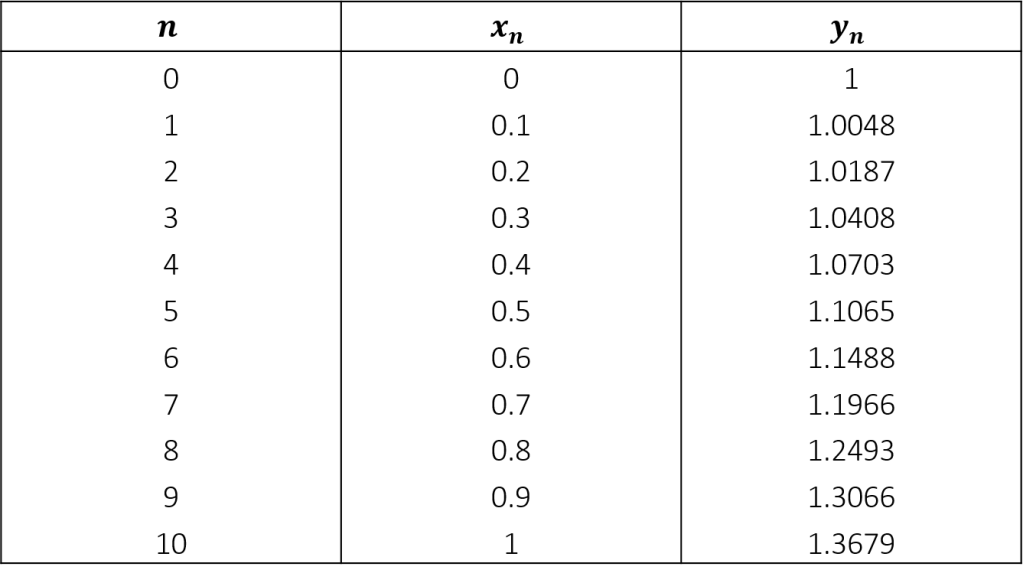
Extrayendo los resultados obtenidos durante el método de Heun, se muestran en la siguiente tabla.

Resolviendo la ecuación diferencial, por el método de ecuaciones diferenciales homogéneas y el método de separación de variables

$y^{'} = x - y + 1$

$dy = (x-y+1)dx$

Si $v = x - y$ y $dv = dx - dy$

$dx-dv=(v+1)dx$

$-dv=v \ dx$

$\displaystyle -\frac{dv}{v} = dx$

$\displaystyle -\int{\frac{dv}{v}} = \int{dx}$

$-\ln{v} = x + C$

Regresando a las variables que fueron reemplazadas (es decir, $v = x - y$ ) y despejando la variable « $y$ «

$\ln{(x-y)} = - x + C$

$\displaystyle y = x + Ce^{-x}$

Esta expresión es la solución general de la ecuación diferencial del problema. Utilizando la condición $y(0)=1$ .

$1=0+Ce^{(-0)}$

$C=1$

Entonces, la solución es

$\displaystyle y = x + e^{-x}$

Donde este resultado es la solución particular de la ecuación diferencial del problema. Comparando con los resultados exactos tan solo evaluando la función $y = x + e^{-x}$ .

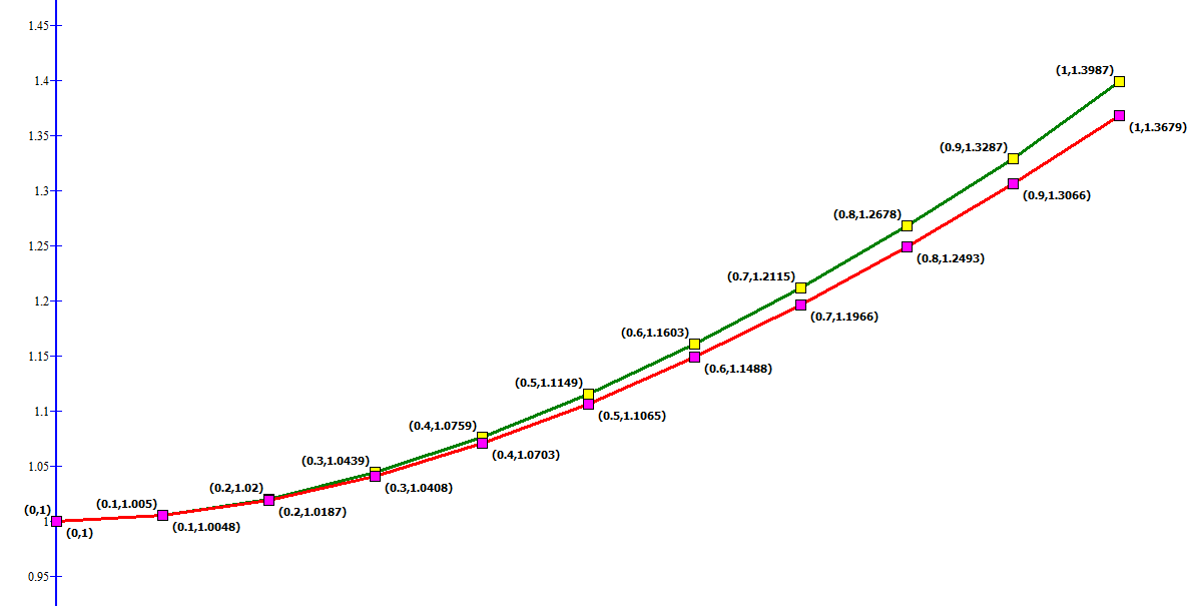
A continuación, la gráfica de todos los puntos; la línea verde es de los resultados obtenidos en el método de Heun y la línea roja es de los resultados obtenidos en la función “ $y$ ” (resuelto la ecuación diferencial).

mn-p1-s-heunimagen1 — Figura 1. Comparación de los valores calculados con el método de Heun (valores aproximado, línea verde) y la tabulación de la solución particular de la ecuación diferencial del problema (valores exactos, línea roja).

Solución de ecuaciones diferenciales lineales de primer orden utilizando el método de Heun. Métodos numéricos.

Introducción

Problema resuelto

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta

Solución de ecuaciones diferenciales lineales de primer orden utilizando el método de Heun. Métodos numéricos.

Introducción

Problema resuelto

Comparte esto:

Relacionado

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta