Teorema del muestreo y el efecto aliasing. Control digital.

Introducción

Si la frecuencia de muestreo es suficientemente alta, comparada con la componente de más alta frecuencia que se incluye en la señal en tiempo continuo, las características de amplitud de la señal en tiempo continuo se pueden preservar en la envolvente de la señal muestreada.

Para reconstruir la señal original a partir de una señal muestreada, existe una frecuencia mínima que la operación de muestreo debe satisfacer.

espectro en una frecuencia — Figura 1. Un espectro en frecuencia.

Teorema del muestreo

Teorema. Si $\omega_s$ , definida como $2\pi /T$ , donde $T$ es el período de muestreo, es mayor que $2\omega_1$ :

$\omega_s > 2\omega_1$

Donde $\omega_1$ es la componente de más alta frecuencia presente en la señal de tiempo continuo $late x(t)$, entonces la señal se puede reconstruir completamente a partir de la señal muestreada.

Para demostrar la validez de teorema del muestreo, se necesita encontrar el espectro en frecuencia de la señal muestreada $x^* (t)$ . Primero:

$\displaystyle X^{*} (s) = \frac{1}{T} \sum_{k=-\infty}^{\infty}{X(s+j\omega_s k)} + \frac{1}{2} x(0+) = \frac{1}{T} \sum_{k=-\infty}^{\infty}{X(s+j\omega_s k)}$

Si $s=j\omega$

$\displaystyle X^{*} (j\omega) = \frac{1}{T} \sum_{k=-\infty}^{\infty}{X(j\omega+j\omega_s k)} = \frac{1}{T} \sum_{k=-\infty}^{\infty}{X(j\omega+\omega_s k)}$

$\displaystyle X^{*} (j\omega) = \cdots + \frac{1}{T} X(j(\omega-\omega_s )) + \frac{1}{T} X(j(\omega)) + \frac{1}{T} X(j(\omega+\omega_s ))+\cdots$

$\displaystyle X^{*} (j\omega) = \cdots + 0 + \frac{1}{T} X(j\omega)+ 0 +\cdots$

$\displaystyle \therefore X^{*} (j\omega) = \frac{1}{T} X(j\omega)$

En la siguiente figura se observa que el espectro en frecuencia de una señal muestreada $x^* (t)$ mediante impulsos se produce un número infinito de veces y se atenúa en un factor de $\displaystyle \frac{1}{T}$ . De esta manera, el proceso de modulación mediante impulsos de una señal en tiempo continuo produce una serie de bandas laterales. Si $X^* (s)$ es periódica con un valor de $\displaystyle \frac{2\pi}{\omega_s}$ :

$X^* (s) = X^* (s \pm j\omega_s k)$ , $k=0, 1, 2, \cdots$

Si una función $X(s)$ tiene un polo en $s=s_1$ , entonces $X^* (s)$ tiene un polo en $s = s_1 \pm j\omega_s k$ ( $k=0, 1, 2, \cdots)$

Si $\omega_s > 2\omega_1$ , las componentes de $|X^* (j\omega)|$ no se traslaparán, y el espectro en frecuencia muestreada se repetirá cada $\omega_s$ (rad/s).

gráfica de esprectos en frecuencia 1 — Figura 2. Gráfica de espectros en frecuencia.

Si $\omega_s < 2\omega_1$ , la forma original de $X(j\omega)$ no parecen más en la gráfica de $|X^* (j\omega)|$ contra ω debido a la superposición de los espectros.

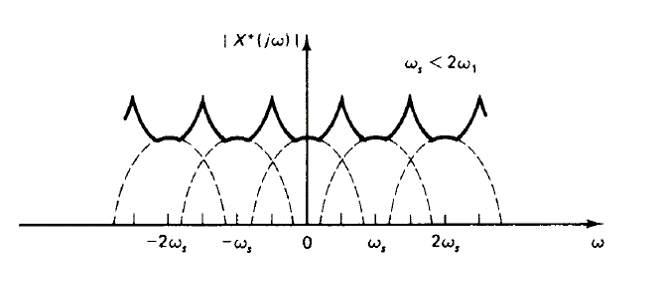
grafica de espectros en frecuencia — Figura 3. Gráfica de espectros en frecuencia.

Efecto aliasing

Este proceso es causado por un muestreo incorrecto de la señal que se está digitalizando, de modo que operan imperfecciones en la misma. Se define científicamente como el efecto que produce cuando una señales continuas distintas se vuelven indistinguibles al muestrearlas digitalmente. Es la alteración de la percepción de un determinado movimiento a través de nuestra percepción o de cualquier óptica.

Se necesitará un filtro antialiasing que limpie la señal antes de hacer una conversión análogo-digital. El propósito del filtro antialiasing es eliminar cualquier presencia de las frecuencias superiores a frecuencia de muestreo/2. Esta mitad de la frecuencia de muestreo viene del “Teorema de muestreo de Nyquist-Shannon”.

Teorema del muestreo y el efecto aliasing. Control digital.

Introducción

Teorema del muestreo

Efecto aliasing

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta

Teorema del muestreo y el efecto aliasing. Control digital.

Introducción

Teorema del muestreo

Efecto aliasing

Comparte esto:

Relacionado

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta