Cálculo de la presión ejercida por un fluido sobre superficies verticales. Cálculo integral.

Introducción

De acuerdo con la física, se sabe que cuanto más profundamente se sumerge un objeto, mayor es la presión que sufre (entendiendo como presión la fuerza ejercida sobre cada unidad de área). La fórmula que se calcula la presión es

$P = \overline{\omega} h$

Donde $P$ es la presión del fluido, $\overline{\omega}$ es la densidad del fluido (peso por unidad de volumen) y $h$ es la altura bajo la superficie (profundidad).

Por ejemplo, como el gramo es el peso de $1 \ \text{cm}^3$ de agua, el peso de $1 \ \text{m}^3$ es $1000 \ \text{kg}$ . Además, la densidad del agua es de $62.4 \ \text{ libras}/\text{pie}^3$ y por tanto, a una profundidad de 9 pies, la presión sobre un objeto sumergido es

$\displaystyle P = \overline{\omega} h$

$\displaystyle P = (62.4 \, \frac{\text{libras}}{\text{pie}^3})(9 \ \text{pies})$

$\displaystyle P = 561.6 \, \frac{\text{libras}}{\text{pie}^2}$

Esta presión corresponde al peso de la columna de agua de 9 pies de altura que soporta sobre sí cada pie cuadrado de área del objeto. Además, de acuerdo con el principio de Pascal, la presión ejercida por un fluido a una determinada profundidad es igual en todas direcciones. Entonces, la presión contra la pared del contenedor, a cierta profundidad, es igual a la ejercida sobre un objeto sumergido a la misma profundidad. De lo anterior se deduce que la presión ejercida por un fluido es independiente de la forma del recipiente. Esto quiere decir que 4 metros por debajo de la superficie, la presión sobre la pared de una piscina es igual a la que se ejerce sobre el frontal de una presa, supuesta una idéntica densidad del agua. La presión queda determinada por la profundidad únicamente; cualquier otra dimensión del contenedor es irrelevante. La mayor atención sobre el conocimiento de la presión de fluidos recae en el cálculo de la presión total ejercida por un fluido sobre las paredes de un contenedor. Si el contenedor es de paredes verticales, resulta fácil calcular la presión total sobre su fondo. La presión en el fondo es constante, y la presión total es el producto de dicha presión por el área del fondo. En general, para una región plana sumergida horizontalmente, se tiene que

$\displaystyle P = \overline{\omega}hA$

Donde $P$ es la presión total sobre una región plana, $\overline{\omega}$ es la densidad del fluido, $h$ es la altura bajo la superficie (profundidad), $A$ es el área de la región plana.

Si se desea calcular la presión total sobre las paredes verticales de un contenedor, se encuentra que la presión no es constante en cada punto, sino que crece con la profundidad.

Si $ABCD$ (de la figura 1) representa una parte de la superficie vertical de una pared de un aljibe, y si se desea conocer la presión total del fluido sobre dicha superficie, se trazan los ejes coordenados tal y como está indicado en la figura 1, ubicando el eje y sobre la superficie del fluido. Luego, se divide $AB$ en $n$ subintervalos y se construyen rectángulos horizontales dentro de la superficie $ABCD$ .

El área de uno, cualquiera, de los rectángulos (como $EP$ ) es $y \, \Delta x$ . Si este rectángulo fuese horizontal a la profundidad $x$ , la presión del fluido sobre él sería

$\displaystyle P = \overline{\omega} x \, y\Delta x$

Por el principio de Pascal, $P = \overline{\omega} x \, y\Delta x$ es, aproximadamente, la presión sobre el rectángulo $EP$ en su posición vertical. Por tanto, la suma

$\displaystyle \sum_{i=1}^n{\overline{\omega} {x}_{1} y_1 \Delta x_1}$

representa, aproximadamente, la presión sobre todos los rectángulos.

La presión sobre la superficie $ABCD$ es el límite de la suma y, por el teorema fundamental del cálculo integral, se tiene que

$\displaystyle \lim_{n \rightarrow \infty}{\sum_{i=1}^{n}{\overline{\omega} x_1 y_1 \Delta x_1}} = \int{\overline{\omega}x y \, dx}$

Por tanto, la presión de un fluido sobre una superficie vertical sumergida limitada por una curva, el eje x y las dos rectas horizontales $x=a$ y $x=b$ , se obtiene con la fórmula

$\displaystyle P = \overline{\omega} \int_a^b{xy \, dx}$

El valor de $y$ ha de sustituirse en términos de $x$ , deducido de la ecuación de la curva dada.

Problemas resueltos

Problema 1. Una cañería circular de 4 m de diámetro (figura 2) está medio llena de agua. Calcular la presión sobre la compuerta que cierra dicha cañería.

Solución. La ecuación del círculo es

$x^2+y^2=4$

Despejando $y$

$\displaystyle y = \pm \sqrt{4-x^2}$

Tomando sólo la parte positiva de la raíz cuadrada

$\displaystyle y = \sqrt{4-x^2}$

Como el gramo es el peso de $1 \, \text{cm}^3$ de agua, el peso de $1 \, \text{m}^3$ es de $1000 \, \text{kg}$ . Entonces $\overline{\omega} = 1000 \, \text{kg} / \text{m}^3$ . Los límites son $x=0$ y $x=2$ ; así, la presión a la derecha del eje $x$ es

$\displaystyle P = \overline{\omega} \int_a^b{xy \, dx} = 1000 \int_0^2{x \sqrt{4-x^2} \, dx}$

$\displaystyle P = 1000 \left[-\frac{1}{3} (4-x^2 )^{\frac{3}{2}} + C\right]_0^2 = 1000 \left[-\frac{1}{3} (4-2^2 )^{\frac{3}{2}} + C \right] - 1000 \left[-\frac{1}{3} (4-0^2)^{\frac{3}{2}} + C\right]$

$\displaystyle P = -1000 \left(-\frac{8}{3} \right) = \frac{8000}{3} \, kg$

Finalmente

$\displaystyle P_{\text{total}} = 2P = 2 \left(\frac{8000}{3} \, \text{kg} \right) = \frac{16000}{3} \, \text{kg}$

$\displaystyle \therefore P_{\text{total}} = \frac{16000}{3} \, \text{kg}$

La presión total sobre la compuerta que cierra la cañería es de 5333.333 kg.

Problema 2. Una presa tiene una compuerta vertical en forma de trapecio (figura 3) que mide 12 m en su lado superior, 8 m en su base y 4m de altura. ¿Cuál es la fuerza total ejercida sobre la compuerta si su lado superior está 4 m bajo la superficie del agua?

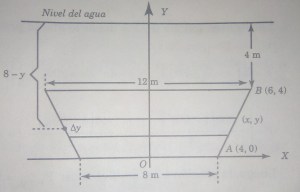
Solución. Con base en la figura 3, se tiene que

$dA=2x \, dy$

$h=8-y$

$\displaystyle dP = \overline{\omega} (8-y)2x \, dy$

Determinando la ecuación de la recta $AB$ , se tiene lo siguiente

$y - y_1 = m_{\tan} (x - x_1 )$

$\displaystyle y - y_1 = \left(\frac{y_2-y_1}{x_2-x_1} \right) (x-x_1 )$

$\displaystyle y - 0 = \left(\frac{4-0}{6-4} \right)(x-4)$

$y=2x-8$

Luego, despejando la variable x en la ecuación de la recta $AB$

$y=2x-8$

$2x=y+8$

$\displaystyle x = \frac{1}{2} y + 4$

Sustituyendo en $dP$

$\displaystyle dP = \overline{\omega}(8-y)2x \, dy$

$\displaystyle dP = \overline{\omega}(8-y)2(\frac{1}{2} y + 4) \, dy$

$\displaystyle dP = \overline{\omega}(8-y)(y+8) \, dy$

$\displaystyle dP = \overline{\omega}(64-y^2 ) \, dy$

Integrando en ambos miembros

$\displaystyle P = \int_0^4{\overline{\omega}(64-y^2 ) \, dy}$

$\displaystyle P = \overline{\omega} \int_0^4{(64-y^2 ) \, dy} = \overline{\omega} \left[64y - \frac{1}{3} y^3 + C\right]_0^4$

$\displaystyle P = \overline{\omega} \left\{ \left[64(4) - \frac{1}{3} (4)^3 \right] - \left[64(0) - \frac{1}{3} (0)^3 \right] \right\}$

$\displaystyle P = \overline{\omega} \left(256-\frac{64}{3} - 0 \right) = \frac{704}{3} \overline{\omega}$

Si $\overline{\omega} = 1000 \, \text{kg} / \text{m}^2$ , el resultado final es

$\displaystyle P = \frac{704}{3} \overline{\omega}$

$\displaystyle P = \frac{704}{3} (1000)$

$\therefore P = \frac{704000}{3} \approx 234666.667 \, \text{kg}$

Problema 3. Cada uno de los extremos de un tanque horizontal es una elipse cuyo eje horizontal es de 4 m y el eje vertical de 2 m. Calcular la presión sobre un extremo cuando el tanque está medio lleno de petróleo que pesa 800 $\text{kg} / \text{m}^3$ .

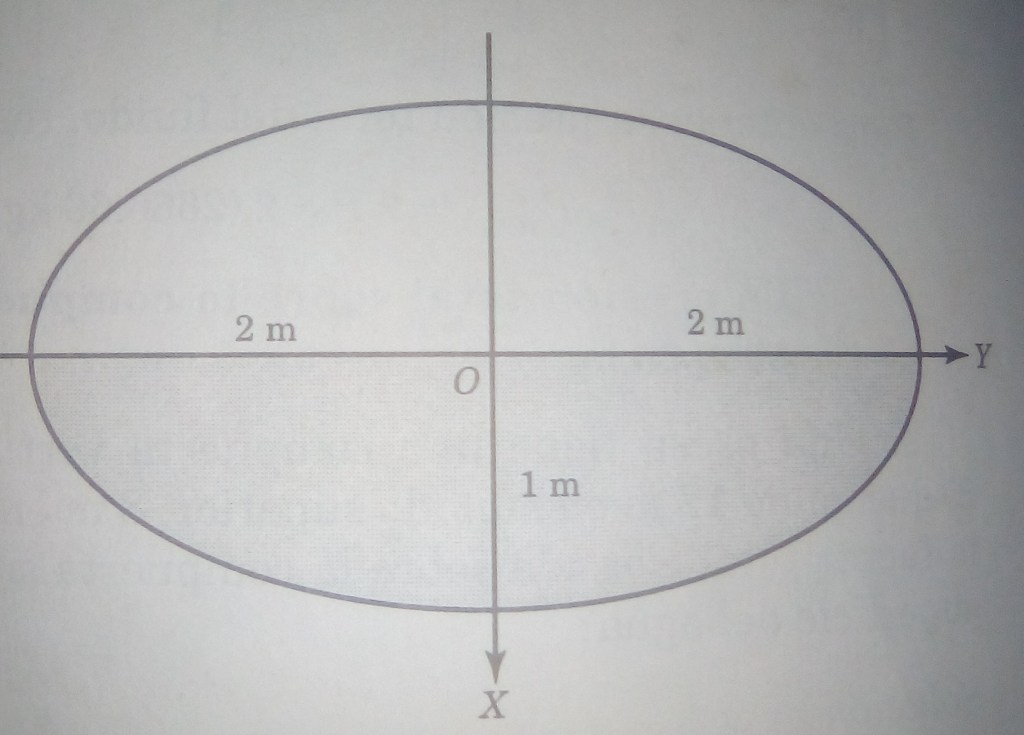
Solución. Con base en la figura 4, corresponde a una elipse, por lo que su ecuación canónica es

$\displaystyle \frac{x^2}{b^2} + \frac{y^2}{a^2} = 1$

Si $a=2$ y $b=1$

$\displaystyle x^2 + \frac{y^2}{4} = 1$

Despejando la variable $y$

$\displaystyle \frac{y^2}{4} = 1-x^2$

$y^2=4(1-x^2 )$

$\displaystyle y = \pm 2 \sqrt{1-x^2}$

$\displaystyle y = 2 \sqrt{1-x^2}$

Los límites a tomar son $x=0$ y $x=2$ , por lo que la presión a la derecha del eje $x$ es

$\displaystyle P = \overline{\omega} \int_a^b{xy \, dx}$

$\displaystyle P = \overline{\omega} \int_0^1{x \cdot 2 \sqrt{1-x^2} \, dx} = 2\overline{\omega} \int_0^1{x \sqrt{1-x^2} \, dx}$

$\displaystyle P = 2\overline{\omega} \left[-\frac{1}{3} (1-x^2 )^{\frac{3}{2}} + C\right]_0^1 = 2\overline{\omega} \left\{\left[-\frac{1}{3} (1-1^2)^{\frac{3}{2}} \right] - \left[-\frac{1}{3} (1-0^2)^{\frac{3}{2}} \right] \right\}$

$\displaystyle P = 2\overline{\omega} \left[(0) - \left(-\frac{1}{3} \right) \right] = \frac{2}{3} \overline{\omega}$

Si $\overline{\omega} = 800 \, \text{kg} / \text{m}^3$

$\displaystyle P = \frac{2}{3} \overline{\omega}$

$\displaystyle P = \frac{2}{3} (800) = \frac{1600}{3} \ \text{kg}$

Finalmente, la presión total del fluido es de

$\displaystyle P_{\text{total}} = 2P$

$\displaystyle P_{\text{total}} = 2 \left(\frac{1600}{3} \right) = \frac{3200}{3} \ \text{kg}$

$\displaystyle \therefore P_{\text{total}} = \frac{3200}{3} \ \text{kg} = 1066.667 \, kg$

La presión sobre un extremo del tanque es de 1066.667 kg.

Problema 4. Una superficie plana, cuya forma es la de un segmento parabólico de 12 m de base y 4 m de altura, está sumergida en el agua de manera que su base se encuentra en la superficie libre del líquido. Calcular la fuerza ejercida sobre una de las caras de la superficie.

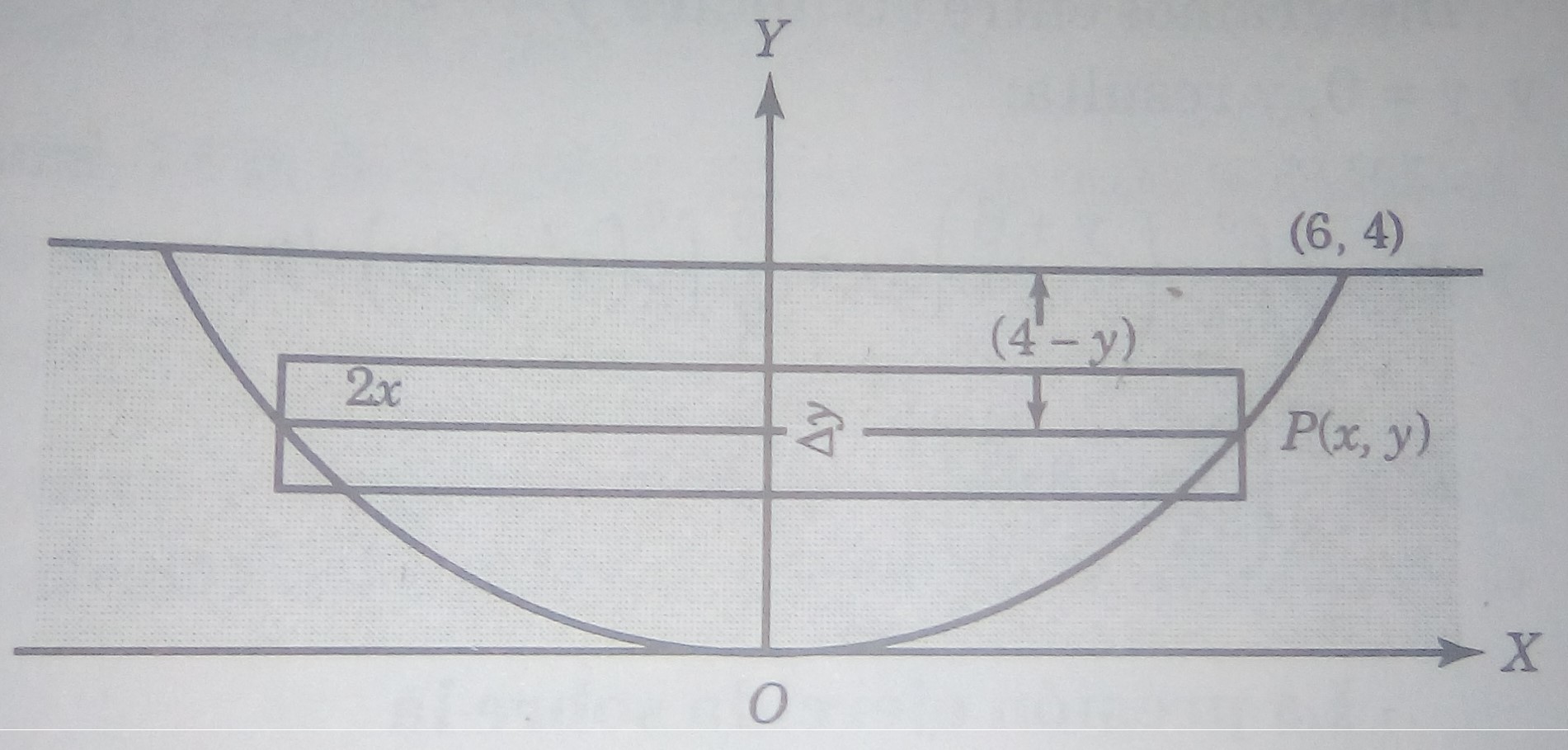
Solución. Con base en la figura 5, se denota que la ecuación canónica de la parábola es

$x^2=4py$

Sustituyendo el punto $(6,4)$ dentro de la ecuación de la parábola, resulta que

$6^2=4p(4)$

$36=16p$

$\displaystyle p = \frac{36}{16}$

$\displaystyle p = \frac{9}{4}$

así, la ecuación del segmento parabólico es

$\displaystyle x^2=4py$

$\displaystyle x^2 = 4(\frac{9}{4})y$

$\displaystyle x^2=9y$

Despejando $x$

$\displaystyle x = \pm \sqrt{9}y$

$\displaystyle x = 3\sqrt{y}$

El área del rectángulo genérico es 2x ∆y; la profundidad de su centro geométrico es $(4-y)$ . Sean los límites $y=0$ y $y=4$ . Aplicando la fórmula $P=\overline{\omega}hA$ , resulta

$\displaystyle P = \overline{\omega}hA$

$\displaystyle P = \overline{\omega}(4-y)2x \, \Delta y$

$\displaystyle P = \overline{\omega}(4-y)2(3\sqrt{y})\Delta y$

$\displaystyle P = 6\overline{\omega}(4y^{\frac{1}{2}} - y^{\frac{3}{2}} ) \Delta y$

Integrando

$\displaystyle P = \int_0^4{6\overline{\omega} (4y^{\frac{1}{2}} - y^{\frac{3}{2}}) \, dy} = 6\overline{\omega} \int_0^4{(4y^{\frac{1}{2}} - y^{\frac{3}{2}}) \, dy}$

$\displaystyle P = 6 \overline{\omega} \left[\frac{8}{3} y^{\frac{3}{2}} - \frac{2}{5} y^{\frac{5}{2}} + C \right]_0^4 = 6\overline{\omega} \left\{\left[\frac{8}{3} (4)^{\frac{3}{2}} - \frac{2}{5} (4)^{\frac{5}{2}} \right] - \left[\frac{8}{3} (0)^{\frac{3}{2}} - \frac{2}{5} (0)^{\frac{5}{2}} \right] \right\}$

$\displaystyle P = 6\overline{\omega} \left(\frac{64}{3} - \frac{64}{5} \right) = \frac{256}{5} \overline{\omega}$

Si $\overline{\omega} = 1000 \, \text{kg}/ \text{m}^3$ , resulta

$\displaystyle P = \frac{256}{5} \overline{\omega}$

$\displaystyle P = \frac{256}{5} (1000) = \frac{256000}{5} = 51200 \, \text{kg}$

$\displaystyle \therefore P=51200 \, \text{kg}$

La fuerza ejercida sobre una de las caras de la superficie es de 51200 kg.

Problema 5. En el siguiente problema el eje y se dirige verticalmente hacia arriba, y el eje x está al nivel de la superficie de un fluido. El peso de la unidad cúbica del fluido está representado por $\overline{\omega}$ . Calcular la presión ejercida sobre la superficie que se forma uniendo con líneas rectas la serie de puntos, en el orden dado: (0,0), (3,0), (0,-6) y (0,0).

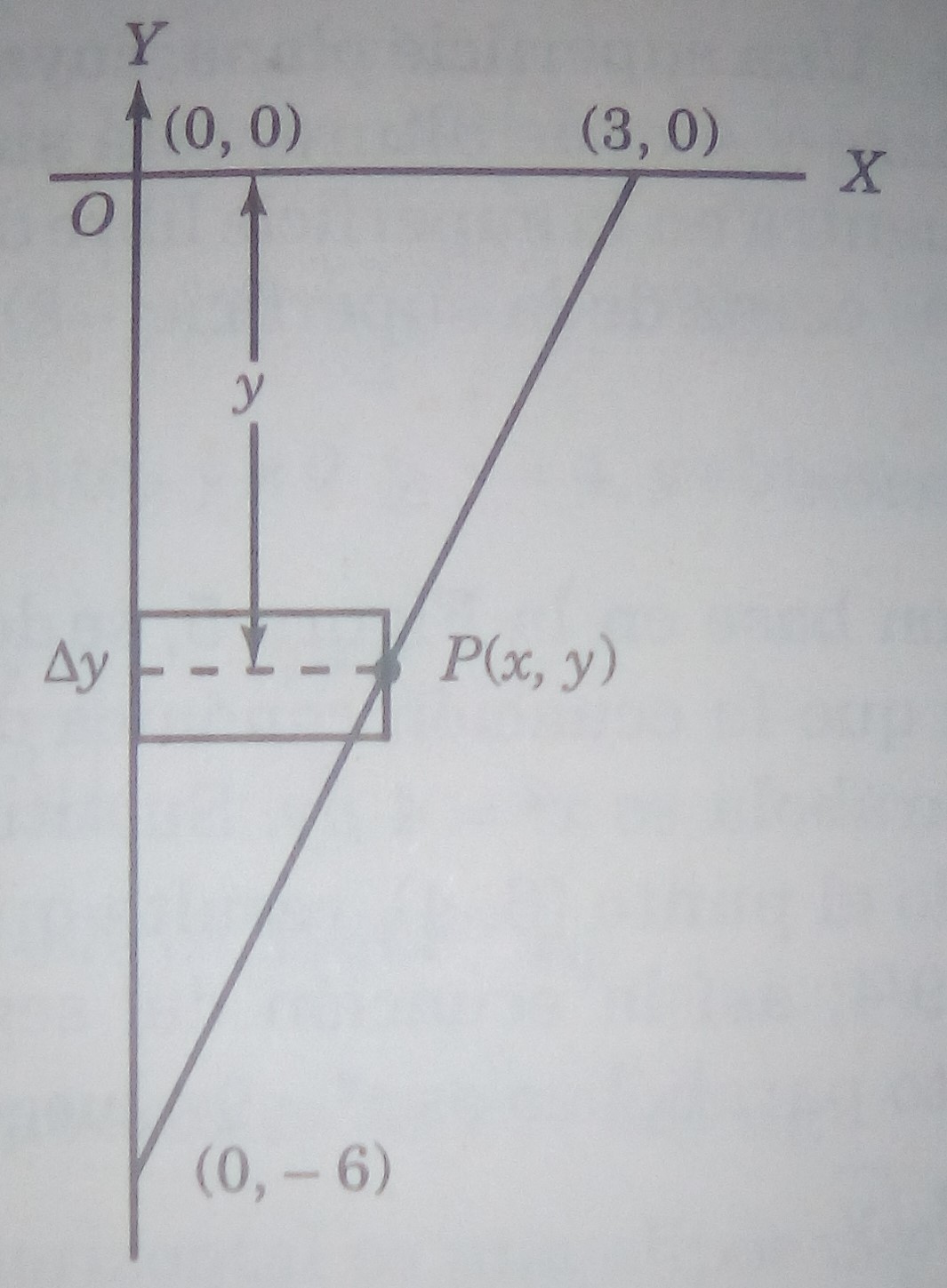
Solución. Con base en la figura 6, se denota que la superficie sumergida está acotada por las rectas $x=0$ , $y=0$ y $2x-y-6=0$ .

Despejando la variable $x$ de la ecuación $2x-y-6=0$

$2x-y-6=0$

$2x=y+6$

$\displaystyle x = \frac{y+6}{2}$

El área del rectángulo genérico es $x \, \Delta y$ , y la profundidad es $y$ .

Aplicando la fórmula $P=\overline{\omega}hA$ , se tiene lo siguiente

$\displaystyle P = \overline{\omega}y \, x\Delta y$

$\displaystyle P = \overline{\omega}y \left(\frac{y+6}{2} \right) \Delta y$

Integrando entre los límites $y=-6$ y $y=0$ , y resulta

$\displaystyle P = \int_{-6}^0{\overline{\omega} y \left( \frac{y+6}{2} \right) \, dy} = \frac{\overline{\omega}}{2} \int_{-6}^0{y(y+6) \, dy}$

$\displaystyle P = \frac{\overline{\omega}}{2} \int_{-6}^0{(y^2+6y) \, dy} = \frac{\overline{\omega}}{2} \left[\frac{1}{3} y^3 + 3y^2+ C \right]_{-6}^0$

$\displaystyle P = \frac{\overline{\omega}}{2} \left\{\left[\frac{1}{3} (0)^3 + 3(0)^2 \right] - \left[\frac{1}{3} (-6)^3 + 3(-6)^2 \right] \right\}$

$\displaystyle P = \frac{\overline{\omega}}{2} \left\{(0) - \left[\frac{1}{3} (-216) + 3(36) \right] \right\}$

$\displaystyle P = \frac{\overline{\omega}}{2} \left[0 - (-72+108) \right] = \frac{\overline{\omega}}{2} (-36) = -18\overline{\omega}$

Finalmente

$\therefore P = 18 \overline{\omega}$

La presión ejercida sobre la superficie es de $18\overline{\omega}$ .

Cálculo de la presión ejercida por un fluido sobre superficies verticales. Cálculo integral.

Introducción

Problemas resueltos

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta

Cálculo de la presión ejercida por un fluido sobre superficies verticales. Cálculo integral.

Introducción

Problemas resueltos

Comparte esto:

Relacionado

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta