Cálculo del trabajo realizado por una fuerza variable. Cálculo integral.

Trabajo realizado por una fuerza constante

Para los científicos e ingenieros, el concepto de trabajo resulta ser importante al momento de calcular la energía requerida para realizar algunas tareas de tipo físico. Por ejemplo, es útil saber la cantidad de trabajo desarrollado al elevar una viga con una grúa, al comprimir un muelle, cuando un camión transporta una carga o al disparar un rifle.

En general, se establece que se ha realizado un trabajo cada vez que una fuerza aplicada mueve un objeto cierta distancia; el trabajo realizado por esa fuerza se define como

$\displaystyle T=F \cdot d$

El trabajo puede expresarse en distintas unidades (libras por pies, libras por pulgada, kg por cm, etc.) En el sistema métrico, las unidades fundamentales de trabajo son dina por cm (erg) y el N por m (J, es decir, joule), donde $1 \, J =10^7 \, \text{ergs}$ .

Problemas resueltos

Problema 1. Calcular el trabajo realizado al levantar un objeto de 150 kg con una altura de 4 m.

Solución. Si la fuerza es de 150 kg y la distancia de 4 m (medido desde el suelo hasta la parte final el objeto), el trabajo realizado es

$T = F \cdot d$

$T = (150 \, \text{kg})(4 \, \text{m})$

$\displaystyle T = 600 \, \frac{\text{kg}}{\text{m}}$

Finalmente, el trabajo realizado al levantar un objeto es de 600 kg/m.

Trabajo realizado por una fuerza variable

Al aplicar una fuerza variable a un objeto, la determinación del trabajo realizado se obtiene por los métodos del cálculo integral, debido a que la fuerza necesaria para mover el objeto cambia al variar la posición de dicho objeto. Entonces, la fuerza requerida para comprimir un resorte crece conforme se comprime dicho resorte. Ahora se analizará el trabajo que se realiza al vaciar un aljibe (trabajo de bombeo) cuya forma es de un sólido de revolución con eje vertical. Se va a suponer que el eje x de la cuerva que gira sea vertical y que el eje y esté en el plano de la parte superior del aljibe; tal como se muestra en la figura 4.10.1. Se debe calcular el trabajo que se realiza al variarlo, si la superficie del líquido pasa de la profundidad a hasta la profundidad b.

Dividiendo $AB$ en $n$ subintervalos, por estos puntos de división se hacen pasar planos perpendiculares al eje de revolución que constituyen cilindros de revolución.

El volumen de uno, cualquiera, de dichos cilindros es $\pi y^2 \Delta x$ y $\overline{\omega}$ es el peso de la unidad cúbica del líquido; resulta

$\overline{\omega} \pi y^2 \Delta x$

El trabajo que se efectúa al subir un peso es igual al producto del peso por la altura vertical; por tanto, el trabajo de subir dicho cilindro de líquido a la altura $x$ es $\overline{\omega} \pi y^2 \, x\Delta x$ . La suma del trabajo realizado al subir todos estos cilindros es

$\displaystyle \sum_{i=1}^n{\overline{\omega} \pi y_i^2 x_i \Delta x_i}$

El trabajo efectuado al vaciar la parte $AB$ del aljibe es, lógicamente, el límite de dicha suma y, por el teorema fundamental del cálculo integral, resulta

$\displaystyle \lim_{n \rightarrow \infty}{\sum_{i=1}^n{\overline{\omega} \pi y_i^2 x_i \Delta x_i }} = \int{\overline{\omega} \pi y^2 x \, dx}$

Entonces, el trabajo efectuado al vaciar un aljibe en forma de un sólido de revolución, de tal manera que la superficie del líquido pase desde la profundidad a hasta la profundidad b, está dado por la fórmula:

$\displaystyle T = \overline{\omega} \pi \int_a^b{y^2 \, dx}$

Aquí el valor de $y$ ha de sustituirse en términos de x obtenido de la ecuación de la curva que gira.

El principio fundamental para este razonamiento es que el elemento de trabajo ( $dT$ ) que se realiza al levantar un elemento ( $dV$ ) de volumen a una altura h es

$\displaystyle dT = \overline{\omega} h \, dV$

Tomando en cuenta lo anterior, se puede elegir los ejes de coordenadas de cualquier modo que convenga.

Problemas resueltos

Problema 1. Calcular el trabajo que se realiza al bombear el agua que llena su aljibe hemisférico de 5 m de profundidad (figura 2).

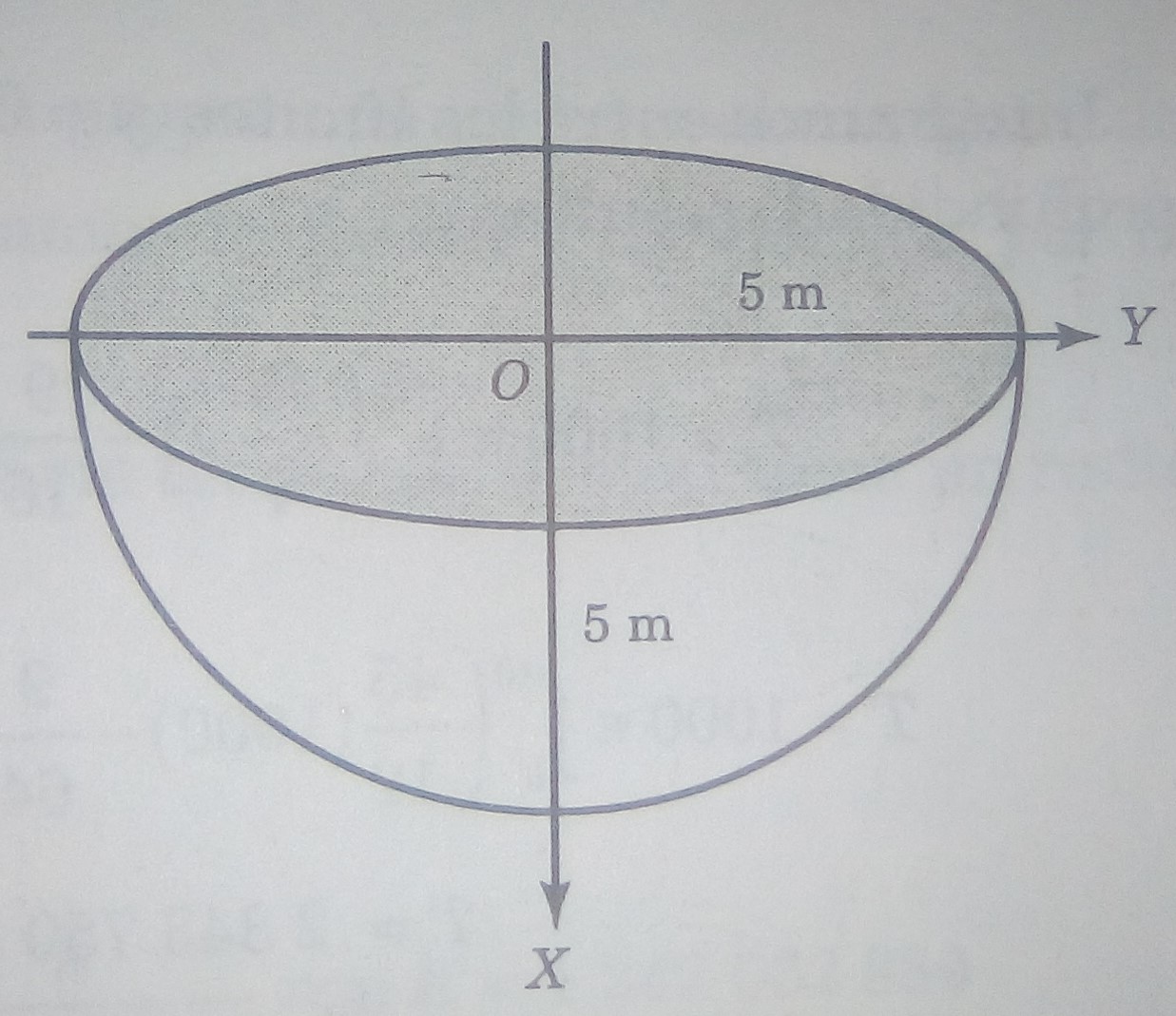
Solución. De la figura 2, la ecuación del círculo es

$x^2+y^2=25$

Despejando $y^2$

$y^2=25-x^2$

Si $\overline{\omega} = 1000$ y los límites inferior y superior son $x=0$ y $x=10$ , el trabajo realizado es

$\displaystyle T = \int_a^b{\overline{\omega}\pi y^2 x \, dx} = \int_0^5{(1000) \pi (25-x^2)x \, dx}$

$\displaystyle T = 1000 \pi \int_0^5{(25x-x^3 ) \, dx} = 1000\pi \left[\frac{25}{2} x^2 - \frac{1}{4} x^4 + C\right]_0^5$

$\displaystyle T = 1000\pi \left\{ \left[ \frac{25}{2} (5)^2 - \frac{1}{4} (5)^4 \right] - \left[\frac{25}{2} (0)^2 - \frac{1}{4} (0)^4 \right] \right\}$

$\displaystyle = 1000\pi \left[\frac{25}{2} (25) - \frac{1}{4} (625) - 0 \right] = 1000\pi (156.25) = 156250 \pi$

Finalmente

$\displaystyle \therefore T = 156250 \pi \, (kg \cdot m)$

Problema 2. Una cisterna cónica tiene 30 m de diámetro superior y 20 m de profundidad. Si la superficie del agua está 10 m más abajo que la parte de arriba, calcular el trabajo que se hace al bombear hasta arriba el agua de la cisterna.

Solución. Por la gráfica, se tiene lo siguiente: $dV = \pi x^2 \, dy$ y altura de $h=20-y$ . Sustituyendo

$\displaystyle dT = \overline{\omega} h \, dV$

$\displaystyle dT = \overline{\omega}(20-y)(\pi x^2 \, dy)$

$\displaystyle dT = \overline{\omega} \pi (20-y) x^2 \, dy$

Luego, la ecuación de la recta $OA$ es

$\displaystyle y - y_1 = m_{\tan} (x-x_1)$

$\displaystyle y - y_1 = \left(\frac{x_2-x_1}{y_2-y_1} \right)(x-x_1 )$

$\displaystyle y-0 = (\frac{20-0}{15-0})(x-0)$

$\displaystyle y = \frac{4}{3} x$

Despejando $x$

$\displaystyle x = \frac{3}{4} y$

Sustituyendo en la ecuación $dT$

$\displaystyle dT = \overline{\omega} \pi (20-y) x^2 \, dy$

$\displaystyle dT = \overline{\omega} \pi (20-y) (\frac{3}{4} y)^2 \, dy$

$\displaystyle dT = \overline{\omega} \pi (20-y)(\frac{9}{16} x^2 ) \, dy$

$\displaystyle dT = \overline{\omega} \pi \left(\frac{180}{16} y^2 - \frac{9}{16} y^3 \right) \, dy$

Integrando entre los límites $y=0$ y $y=10$ (debido a que el agua tiene 10 m de profundidad) con $\overline{\omega} = 1000$ , resulta que

$\displaystyle T = \int_0^{10}{(1000)\pi \left(\frac{180}{16} y^2 - \frac{9}{16} y^3 \right) \, dy} = 1000\pi \left[\frac{180}{48} y^3 - \frac{9}{64} y^4 + C\right]_0^{10}$

$\displaystyle T = 1000\pi \left\{\left[\frac{180}{48} (10)^3 - \frac{9}{64} (10)^4 \right] - \left[\frac{180}{48} (0)^3 - \frac{9}{64} (0)^4\right] \right\}$

$\displaystyle T = 1000\pi \left[\frac{180}{48} (1000) - \frac{9}{64} (10000) - 0 \right]$

$\displaystyle T = 1000\pi \left(\frac{180000}{48} - \frac{90000}{64} \right) = 1000\pi \left(\frac{9375}{4} \right) = 2343750\pi$

Finalmente

$\displaystyle \therefore T =2343750\pi \, \text{kg} \cdot \text{m}$

Problema 3. Para comprimir un resorte desde una longitud natural de 15 cm hasta 12 cm, se requiere una fuerza de 75 kg. Calcular el trabajo realizado al comprimirlo 3 cm más (aplicar la ley de Hooke).

Solución. Por la ley de Hooke, se estable que la fuerza $F(x)$ necesaria para comprimir o extender un resorte $x$ unidades desde su longitud natural es $F(x)=kx$ , donde $k$ es una constante que depende del resorte en cuestión.

Entonces

$F(x)=kx$

$F(3)=k(3)$

$75=k(3)$

$k=25$

Luego, sustituyendo en la ecuación de Hooke

$F(x)=25x$

Para calcular el incremento de trabajo, se supondrá que la fuerza requerida para comprimir el resorte en $\Delta x$ es constante.

Entonces el incremento de trabajo es

∆T = (fuerza)(incremento de d)

$\Delta T = (25x)\Delta x$

Puesto que el resorte se comprime entre $x=3$ y $x=6$ cm menos que su longitud natural, el trabajo realizado es

$\displaystyle T = \int_3^6{25x \, dx}$

$\displaystyle T = 25 \int_3^6{x \, dx} = 25 \left[\frac{1}{2} x^2 + C\right]_3^6$

$\displaystyle T = 25 \left[\frac{1}{2} (6)^2 - \frac{1}{2} (3)^2 \right] = 25 (18 - 4.5)$

$T = 25 (13.5) = 337.5 \, \text{kg} \cdot \text{cm}$

Finalmente

$\therefore T = 337.5 \, \text{kg} \cdot \text{cm}$

Problema 4. Si un módulo espacial pesa 30 toneladas en la superficie terrestre, entonces, despreciando la resistencia del aire, ¿cuánto trabajo se requiere para elevarlo hasta una altura de 2500 km?

Solución. Como el peso de un cuerpo varía en proporción inversa al cuadrado de su distancia al centro de la tierra, se expresa la fuerza $F(x)$ ejercida por la gravedad mediante

$\displaystyle F(x) = \frac{k}{x^2}$

El módulo pesa 30 toneladas en la superficie terrestre, la cual tiene un radio aproximado de 6436 km.

Sustituyendo

$\displaystyle F(x) = \frac{k}{x^2}$

$\displaystyle 30 = \frac{k}{(6436)^2}$

$k=1242662880$

Por lo que

$\displaystyle F(x) = \frac{1 242 662 880}{x^2}$

Entonces el incremento de trabajo es

∆T=(fuerza)(incremento de d)

$\displaystyle \Delta T = \frac{1 242 662 880}{x^2} \Delta x$

Al propulsar el módulo desde 6436 hasta 8936 km, el trabajo desarrollado es

$\displaystyle T = \int_{6436}^{8936}{\frac{1 242 662 880}{x^2} \, dx} = 1 242 662 880 \int_{6436}^{8936}{\frac{1}{x^2} \, dx}$

$\displaystyle T = 1 242 662 880 \left[-\frac{1}{x} + C \right]_{6436}^{8936}$

$\displaystyle T = 1 242 662 880 \left[-\frac{1}{8936} - \left(-\frac{1}{6436} \right) \right] \approx 54017.457$

$\therefore T =$ 54017.575 toneladas ⋅ km

Problema 5. El depósito de la figura 3 tiene 8 m de altura y 2 m de radio en su parte superior. Si se llena hasta una altura de 6 m con un líquido que pesa 50 $kg/m^3$ , calcular el trabajo necesario para bombear todo ese líquido sobre el borde superior del depósito.

Solución. Considerando el líquido subdividido en capas de anchura $\Delta y$ , se puede determinar el trabajo requerido para bombear cada capa, describiendo principalmente el peso de dicha capa como el incremento de fuerza.

∆F = peso

∆F = (peso)(incremento de la capa)

$\Delta F = (50)(\pi r^2 h)$

Aquí $r=x$ es el radio y $h=\Delta y$ es la altura.

Entonces, como $y=2x^2$ , es decir, $\displaystyle x^2 = \frac{y}{2}$ , se tiene que

$\displaystyle \Delta F = (50)(\pi r^2 h) = (50)(\pi x^2 h) = (50)(\pi \frac{y}{2} \Delta y) = 25\pi y \, \Delta y$

Puesto que cada capa se desplaza $8-y$ metros, el incremento de trabajo es

∆T = (incremento de fuerza)(distancia)

$\Delta T = \Delta F \cdot d$

$\displaystyle Delta T = (25\pi y \Delta y)(8-y)$

$\displaystyle \Delta T = 25\pi (8y-y^2 ) \, dy$

Puesto que las alturas de las diversas capas van desde $y=0$ hasta $y=6$ , el trabajo requerido para vaciar el depósito es

$\displaystyle T = \int_0^6{25\pi (8y-y^2) \, dy} = 25\pi \int_0^6{(8y-y^2) \, dy}$

$\displaystyle T = 25\pi \left[4y^2 - \frac{1}{3} y^3 + C \right]_0^6 = 25\pi \left\{ \left[4(6)^2 - \frac{1}{3} (6)^3 \right] - \left[4(0)^2 - \frac{1}{3} (0)^3 \right] \right\}$

$\displaystyle T = 25\pi \left(144 - \frac{216}{3} - 0 \right) = 25\pi (72) = 1800\pi$

Finalmente

$\displaystyle \therefore T = 1800\pi \approx 5654.88 \, kg \cdot m$

Trabajo de un gas al dilatarse

Si al dilatarse un gas en un cilindro empuja la cabeza de un émbolo de manera que el volumen del gas pase del volumen inicial en metros cúbicos ( $V_i$ ) hasta el volumen final en metros cúbicos ( $V_f$ ), el trabajo exterior que se realiza es, en kilográmetros

Trabajo $\displaystyle (T) = \int_{V_i}^{V_f}{P \, dV}$

donde $P$ es la presión en $\text{kg} / \text{m}^2$ .

Lo anterior se demuestra si se supondría que el volumen aumenta de $V$ a $VT \, dV$ . Sea $A$ el área de la sección transversal del cilindro. Entonces $\displaystyle \frac{dV}{A}$ es la distancia que mueve el émbolo. Dado que $P \, A$ es la fuerza que causa la dilatación $dV$ , se tiene que

$\displaystyle \text{Elemento del trabajo realizado} = PA(\frac{dV}{A}) = P \, dV$

De esta última igualdad se obtiene

$\displaystyle T = \int_{V_i}^{V_f}{P \, dV}$

al aplicar el teorema fundamental del cálculo integral.

Para aplicar $\displaystyle T = \int_{V_i}^{V_f}{P \, dV}$ , debe conocerse la relación entre $P$ y $V$ durante la dilatación. Dicha relación es $PV^n=C$ , siendo $C$ y $n$ constantes.

Al constituirse el diagrama de presión y volumen, con los volúmenes como abscisas y las presiones como ordenadas, el área bajo la curva es numéricamente igual al trabajo que se obtiene con $\displaystyle T = \int_{V_i}^{V_f}{P \, dV}$ .

Dilatación isoterma

Si la temperatura permanece constante, se presenta la dilatación isoterma. Entonces $n=1$ y la relación entre la presión y el volumen es $PV=P_i V_i=P_f V_f$ . Su representación gráfica da lugar a una hipérbola equilátera.

Problemas resueltos

Problema 1. La dilatación del gas contenido en un depósito cilíndrico desplaza un émbolo de manera que el volumen del gas aumenta de 15 a 25 $\text{cm}^2$ . Suponiendo que la relación entre la presión ( $\text{kp} / \text{cm}^2$ ) y el volumen ( $\text{cm}^3$ ) viene dada por $PV^1.4=60$ , calcular el trabajo realizado en la expansión.

Solución. Sea A el área de la sección del cilindro; en dichas condiciones, la fuerza ejercida por el gas es $P \, A$ . Un aumento de volumen $\Delta V$ hace suponer la elevación del pistón $\displaystyle \frac{\Delta V}{A}$ , donde el trabajo correspondiente a dicho desplazamiento es

$\displaystyle PA \left(\frac{\Delta V}{A} \right) = P \Delta V$

De $PV^{1.4}=60$ , se tiene que $\displaystyle P=\frac{60}{V^{1.4}}$ ; luego, $\displaystyle P \Delta V = \left(\frac{60}{V^{1.4}} \right) \Delta V$

Entonces

$\displaystyle T = \int_{15}^{25}{\frac{60}{V^{1.4}} \, dV} = 60\int_{15}^{25}{V^{-1.4} \, dV}$

$\displaystyle T = 60 \left[-\frac{1}{0.4} V^{-0.4} + C\right]_{15}^{25} = 60 \left\{ \left[-\frac{1}{0.4} (25)^{-0.4} \right] - \left[-\frac{1}{0.4} {(15)}^{-0.4} \right] \right\}$

$\therefore T = 9.384 \, \text{kp} \cdot \text{cm}$

Problema 2. Un cilindro contiene un volumen de aire sobre el que se apoya un émbolo. Sabiendo que cuando la presión es de 20 ( $\text{kp} / \text{m}^2$ ) el volumen es de 100 $\text{m}^3$ , calcular el trabajo realizado por el émbolo para comprimir el aire hasta 2 $\text{m}^3$ :

a) Suponiendo que $PV=C$

b) Suponiendo que $PV^{1.4}=C$

Solución del a). Considerando la relación entre la presión y el volumen está dada por $PV=C$ , $\displaystyle (20 \, \frac{\text{kp}}{\text{m}^2} )(100 \, \text{m}^3 )=2000 \, \text{kp} \cdot \text{m}$ .

Si $A$ es el área de la sección del cilindro, en tales condiciones la fuerza ejercida por el gas es $PA$ . Una disminución de volumen $dV$ hacer suponer la compresión del pistón de $\displaystyle \frac{dV}{A}$ , donde el trabajo realizado es

$\displaystyle PA \left(\frac{dV}{A} \right) = P \, dV$

De $PV=2000$ , se tiene $\displaystyle P = \frac{2000}{V}$ ; luego $\displaystyle P \, dV = \left(\frac{2000}{V} \right) \, dV$ . Entonces

$\displaystyle T = \int_{2}^{100}{\frac{2000}{V} \, dV} = \left[2000 \ln{V} + C \right]_2^{100}$

$\displaystyle T = 2000 \ln{100} - 2000 \ln{2} = 7824.046$

$\displaystyle \therefore T = 7824.046 \, kp \cdot m$

Solución del b). Considerando la relación entre la presión y el volumen está dada por $PV^{1.4} = C$ , entonces $\displaystyle \left(20 \, \frac{\text{kp}}{\text{m}^2} \right) (100 \ \text{m}^3 )^{1.4} = 12 619.147 \, \text{kg} \cdot \text{m}$ .

Si $A$ es el área de la sección del cilindro, en tales condiciones fuerza ejercida por el gas es $PA$ . Una disminución de volumen $dV$ hace suponer una compresión del pistón de $\displaystyle \frac{dV}{A}$ , donde el trabajo realizado es

$\displaystyle PA \left(\frac{dV}{A} \right) = P \, dV$

De $PV^{1.4} = 12 619.147$ , se tiene que

$\displaystyle P = \frac{12619.147}{V^{1.4}}$

Luego

$\displaystyle P \, dV = \frac{12619.147}{V^{1.4}} \, dV$

Entonces

$\displaystyle T = \int_2^{100}{\frac{12619.147}{V^{1.4}} \, dV}$

$\displaystyle T = 12619.147 \int_2^{100}{V^{-1.4} \, dV} = -\frac{12619.147}{0.4} \left[V^{-0.4} + C \right]_2^{100}$

$\displaystyle T = -\frac{12619.147}{0.4} \left({100}^{-0.4} - 2^{-0.4} \right) = 18 908.813$

$\displaystyle \therefore T = 18 908.913 \, \text{kp} \cdot \text{m}$

Problema 3. Nueve metros cúbicos de aire a la presión de 2 $kg/cm^2$ se comprimen a la presión de 8 $\text{kg} / \text{cm}^2$ .

a) Calcular el volumen y el trabajo realiza si se aplica la ley isoterma, es decir, $PV=C$ .
b) Calcular el volumen final y el trabajo realizado si se aplica la ley adiabática, es decir, $PV^{1.4}=C$ .

Solución del a). Puesto que $\displaystyle P_i = 2 \ \frac{\text{kg}}{\text{cm}^2}$ , $V_i=9 \, \text{m}^3=9 000 000 \, \text{cm}^3$ y $P_f = 8 \, \frac{\text{kg}}{\text{cm}^2}$ , entonces por

$\displaystyle P_i V_i=P_f V_f$

Se tiene que

$\displaystyle V_f = \frac{P_i V_i}{P_f} = \left(2 \ \frac{\text{kg}}{\text{cm}^2} \right) \frac{9 000 000 cm^3}{8 \frac{\text{kg}}{\text{cm}^2}}$

$\displaystyle \therefore V_f = 2 250 000 \, \text{cm}^3 = 2.25 \, \text{m}^3$

Considerando que la relación entre la presión y el volumen está dada por $PV=C$ , es decir, $\displaystyle \left(2 \, \frac{\text{kg}}{\text{cm}^2} \right)(9 000 000 \, \text{cm}^3) = 18 000 000 \, \text{kg} \cdot \text{cm} = 180 000 \, \text{kg} \cdot \text{m}$ .

De $PV=180 000$ , se tiene que

$\displaystyle P = {180 000}{V}$

Finalmente

$\displaystyle T = \int_{2.25}^{9}{\frac{180 000}{V} \, dV} = 180 000 \left[\ln{V} + C\right]_{2.25}^9$

$\displaystyle = 180000 \ln{9} - 180000 \ln{2.25} = 249 532.985$

$\displaystyle \therefore T = 249 532.985 \ \text{kg} \cdot \text{m}$

Se concluye que el volumen final y el trabajo realizado aplicando la ley isoterma es $2.25 \, \text{m}^3$ y $249 532.985 \, \text{kg} \cdot \text{m}$ , respectivamente.

Solución del b). Puesto que $\displaystyle P_i = 2 \, \frac{\text{kg}}{\text{cm}^2}$ , $V_i = 9 \, \text{m}^3 = 9 000 000 \text{cm}^3$ , $\displaystyle P_f = 8 \, \frac{\text{kg}}{\text{cm}^2}$ , entonces por

$\displaystyle P_i {V_i}^{1.4} = P_f {V_f}^{1.4}$

Despejando $V_f$ se tiene lo siguiente

$\displaystyle V_f = \sqrt[1.4]{P_i \, \frac{{V_i}^{1.4}}{P_f}} = \sqrt[1.4]{2 \cdot \frac{9 000 000^{1.4}}{8}}$

$\displaystyle \therefore V_f = 3 343 487.15 \, \text{cm}^3 = 3.343 \, \text{m}^3$

Considerando que la relación entre la presión y el volumen está dada por $PV^{1.4} = C$ , se tiene que $(2 \, \text{kg}/\text{cm}^2) (9 \, \text{m}^3)^{1.4} = (20 000 \, \text{kg}/\text{m}^2) (9 \, \text{m}^3)^{1.4} = 433 480.443 \, \text{kg} \cdot \text{m}$ .

De $PV^{1.4} = 433 480.443$ , despejando $P$ resulta

$\displaystyle P = \frac{433 480.443}{V^{1.4}}$

Entonces

$\displaystyle T = \int_{3.343}^9{\frac{433 480.443}{V^{1.4}} \, dV} = 433 480.443 \int_{3.343}^9{\frac{dV}{V^{1.4}}}$

$\displaystyle T = 433 480.443 \left[-\frac{1}{0.4} V^{-0.4} + C\right]_{3.343}^9$

$\displaystyle T = 433 480.443 \left[-\frac{1}{0.4} (9)^{-0.4} - \left(-\frac{1}{0.4} {(3.343)}^{-0.4} \right) \right]$

$\displaystyle \therefore T = 218 736.407 \, \text{kg} \cdot \text{m}$

Se concluye que el volumen final y el trabajo realizado aplicando la ley diabática es 3.343 $\text{m}^3$ y 218 736.407 $\text{kg} \cdot \text{m}$ , respectivamente.

Cálculo del trabajo realizado por una fuerza variable. Cálculo integral.

Trabajo realizado por una fuerza constante

Problemas resueltos

Trabajo realizado por una fuerza variable

Problemas resueltos

Trabajo de un gas al dilatarse

Dilatación isoterma

Problemas resueltos

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta

Cálculo del trabajo realizado por una fuerza variable. Cálculo integral.

Trabajo realizado por una fuerza constante

Problemas resueltos

Trabajo realizado por una fuerza variable

Problemas resueltos

Trabajo de un gas al dilatarse

Dilatación isoterma

Problemas resueltos

Comparte esto:

Relacionado

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta