Teoremas

Teorema 1. La transformada de Fourier de una función impulso

\displaystyle \mathcal{F}[\delta (t)] = \int_{-\infty}^{\infty}{\delta (t) e^{-j \omega t} \, dt} = 1

Teorema 2. La transformada inversa de Fourier de una unidad

\displaystyle \delta(t) = \mathcal{F}^{-1}[1] = \frac{1}{2\pi} \int_{-\infty}^{\infty}{e^{j\omega t} \, d\omega}

Nota. Se debe observar que la integral \displaystyle \frac{1}{2\pi} \int_{-\infty}^{\infty}{e^{j\omega t} \, d\omega} no tiene significado en este caso; por lo que, se debe interpretar el dato del teorema 5.1.2 como una función generalizada (o función simbólica), es decir que esta integral converge hacia a \delta(t) en el sentido de la función generalizada.

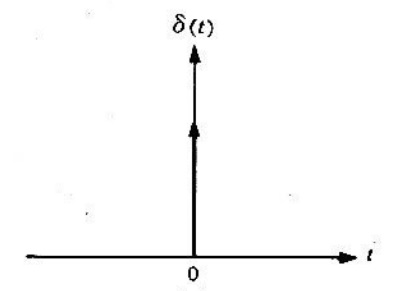
  • Figura 1. Función impulso unitario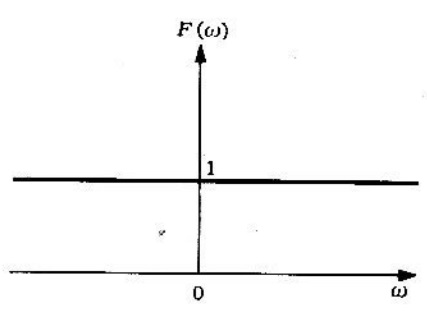
  • Figura 2. Transformada de Fourier de la función impulso unitario

Teorema 3. Representación integral de \delta(t)

\displaystyle \delta(t) = \frac{1}{2\pi} \int_{-\infty}^{\infty}{e^{j\omega t} \, d\omega} = \frac{1}{2\pi} \int_{-\infty}^{\infty}{(\cos{\omega t} + j \sin{\omega t}) \, d\omega} = \frac{1}{\pi} \int_{0}^{\infty}{\cos{\omega t} \, d\omega}

Teorema 4. Expresión general para \delta (y)

\displaystyle \delta(y) = \frac{1}{2\pi} \int_{-\infty}^{\infty}{e^{j x y} \, dx} = \frac{1}{\pi} \int_{0}^{\infty}{\cos{xy} \, dx}

Teorema 5. La transformada de Fourier de la función impulso desplazada \delta (t - t_0)

\displaystyle \mathcal{F}[\delta(t-t_0)] = \int_{-\infty}^{\infty}{\delta (t-t_0) e^{-j \omega t} \, dt} = e^{-j\omega t_0}

Teorema 6. La transformada de inversa de Fourier de la función impulso desplazada e^{-j\omega t_0}

\displaystyle \mathcal{F}^{-1} [e^{-j\omega t_0}] = \frac{1}{2\pi} \int_{-\infty}^{\infty}{e^{-j \omega t_0} e^{j\omega t} \, d\omega} = \frac{1}{2\pi} \int_{-\infty}^{\infty}{e^{j \omega (t - t_0)} \, d\omega} = \delta(t-t_0)

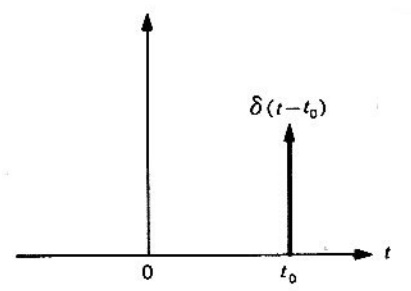
  • Figura 3. Función impulso desplazada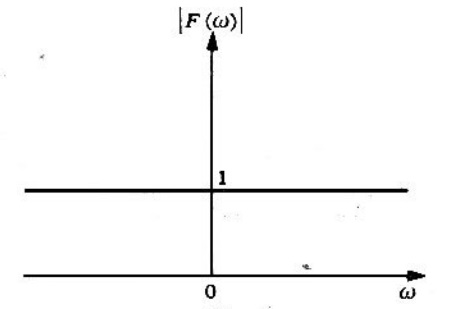
  • Figura 4. Transformada de Fourier de la función impulso desplazada

Alternativa para determinar la fórmula de la inversión de la transformada de Fourier (transformada inversa de Fourier)

Sabiendo que

\displaystyle f(t) = \mathcal{F}^{-1} [F(\omega)]

Entonces

\displaystyle \mathcal{F}^{-1} [F(\omega)] = \frac{1}{2 \pi} \int_{-\infty}^{\infty}{F(\omega) e^{j \omega t} \, d\omega} = \frac{1}{2 \pi} \int_{-\infty}^{\infty}{\left[\int_{-\infty}^{\infty}{f(y) e^{-j \omega y} \, dy} \right] e^{j \omega t} \, d\omega}

Multiplicando

\displaystyle \mathcal{F}^{-1} [F(\omega)] = \frac{1}{2 \pi} \int_{-\infty}^{\infty}{\int_{-\infty}^{\infty}{f(y) e^{-j \omega y} e^{j \omega t} \, dy} \, d\omega}= \frac{1}{2 \pi} \int_{-\infty}^{\infty}{\int_{-\infty}^{\infty}{f(y) e^{(-j \omega y + j \omega t)} \, dy} \, d\omega}

Factorizando las potencias e intercambiando el orden de integración y los parámetros pertenecientes a él

\displaystyle \mathcal{F}^{-1} [F(\omega)] = \frac{1}{2 \pi} \int_{-\infty}^{\infty}{\int_{-\infty}^{\infty}{f(y) e^{j \omega (t-y)} \, dy} \, d\omega}= \int_{-\infty}^{\infty}{f(y) \left[ \frac{1}{2 \pi} \int_{-\infty}^{\infty}{e^{j \omega (t-y)} \, d\omega} \right] \, dy}

Finalmente

\displaystyle \mathcal{F}^{-1} [F(\omega)] = \int_{-\infty}^{\infty}{f(y) \, \delta(t-y) \, dy} = f(t)

Nota. Se ha tomado la variable y como la variable comodín con el fin de no ocasionar confusiones.

Avatar de Desconocido

Publicado por Cesar Reyes

Dedicado a compartir información temas referentes al cálculo básicos, intermedios y avanzados mediante presentaciones PDF, videos y publicaciones en este sitio web.

Deja un comentario

Este sitio utiliza Akismet para reducir el spam. Conoce cómo se procesan los datos de tus comentarios.