Introducción
La función escalón unitario está definido como
Después, se va a suponer que
Se recuerda que , se observa también que
Donde está definido por
Por lo que
excpeto cuando . Por la linealidad de la transformada de Fourier
Ahora, se agrega una nueva suposición
donde es una función ordinaria y
es una constante.
Se recuerda que , por lo que
de donde se concluye que , y
es una función impar.
Para encontrar , se determina de la siguiente manera
Como
Regresando
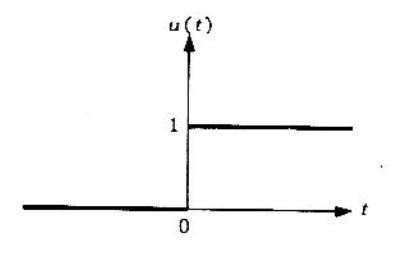
Figura 1. Función escalón unitario. 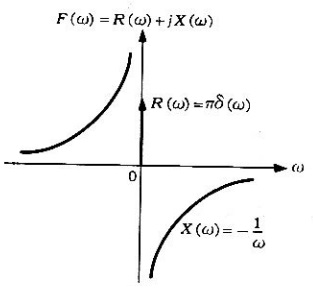
Figura 2. Transformada de Fourier de la función escalón unitario. 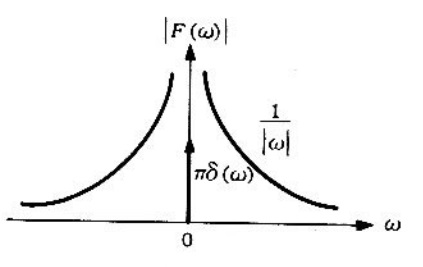
Figura 3. Espectro de la función escalón unitario.
La función signum
Sea y
. La función
se llama signum y está definido como
Como la función es una función impar de la figura 4,
será imaginaria pura, en consecuencia, es una función impar de
.
Ahora, se sabe que
Continuando
Donde es una constante arbitraria. Como
debe ser imaginaria pura impar,
. De donde
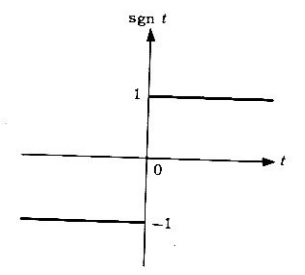
Figura 4. Función sgn t 
Figura 5. Espectro de la función sgn t
Teorema
Teorema 1. Como , se observa que
debido a que .
Entonces, si , por lo tanto