Transformada de Fourier de una función periódica «f(t)»
Una función periódica con período
, se puede expresar como
,
Aplicando la transformada de Fourier en ambos miembros
Esta ecuación establece que la transformada de Fourier de una función periódica, consta de una sucesión de impulsos equidistantes localizados en las frecuencias armónicas de la función.
Teorema 1. La sucesión de pulsos equidistantes
,
,
es la transformada de Fourier de una función periódica con período
.
Demostración. De la transformada de Fourier de una función periódica
la función periódica es
Como , se tiene
;
es decir, es una función periódica con período
Transformada de Fourier de un tren de impulsos unitarios «δT(t)«
El tren de impulsos unitarios está definido como
Como es una función periódica con período
, la serie de Fourier de esa función está dada por
donde , entonces, aplicando la transformada de Fourier en ambos miembros
Este expresión también se puede interpretar de otra manera

Figura 1. Tren de impulsos unitarios. 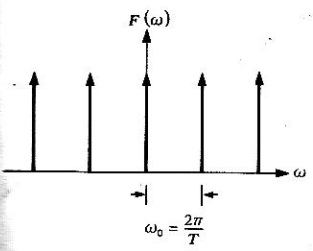
Figura 2. Transformada de Fourier del tren de impulsos unitarios.
Teorema 2. Los coeficientes complejos de la expansión en serie de Fourier de una función periódica
con período
igualan a los valores de la transformada de Fourier
de la función
en
multiplicada por
, donde
está definido por
Demostración. La función periódica con período
se puede expresar como
,
donde
Ahora
Haciendo que , resulta que
Finalmente
Por lo que se concluye que los coeficientes complejos de la expansión en serie de Fourier de una función periódica
con período
igualan a los valores de la transformada de Fourier
de la función
en
multiplicada por
.
Problemas resueltos
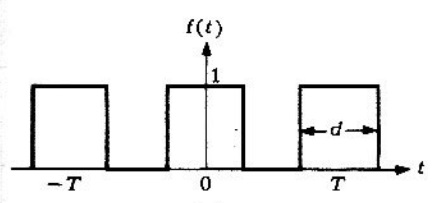
Problema 1. Encontrar los coeficientes complejos de la serie de Fourier de un tren de pulsos rectangulares cuyo ancho es y cuyo período es
, como se muestra en la figura 5.4.3.
Solución. Sea
,
Después, el pulso rectangular definido por
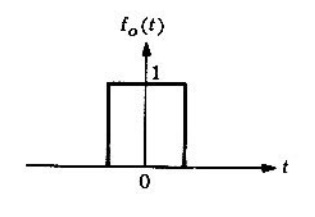
Por lo que su transformada de Fourier es
Por analogía
Cambiando por
, resulta que
Por lo tanto, los coeficientes de la serie de Fourier de
están dados por
Problema 2. Hallar la transformada de Fourier del tren de pulsos rectangulares de ancho y período
, el cual se muestra en la figura 5.

Del resultado obtenido del problema 1
Recordando que
Sustituyendo en la serie de Fourier
Aplicando la transformada de Fourier en ambos miembros
donde .
Este último resultado indica que la transformada de Fourier de un tren de pulsos rectangulares consta de impulsos localizados en , etc. La intensidad del impulso localizado en
está dada por
. El espectro se muestra en la figura 6 (para
).
