Funciones operacionales del sistema. Fourier.

Al denotar $d/dt$ por el operador $p$ , tal que

$\displaystyle p \, f(t) = \frac{d}{dt}[f(t)]$ , $\displaystyle p^n \, f(t) = \frac{d^n}{dt^n}[f(t)]$

Ahora, de la ecuación

$\displaystyle a_n \frac{d^n}{dt^n}[f_o (t)] + a_{n-1} \frac{d^{n-1}}{dt^{n-1}} + \cdots + a_1 \frac{d}{dt}[f_o (t)] + a_0 f_o(t)$

$\displaystyle = b_m \frac{d^m}{dt^m}[f_1 (t)] + b_{m-1} \frac{d^{m-1}}{dt^{m-1}} + \cdots + b_1 \frac{d}{dt}[f_1(t)] + b_0 f_1(t)$

– – – (1)

se puede expresar de la siguiente manera

$\displaystyle \sum_{n=0}^{n}{a_n \frac{d^n}{dt^n} \, [f_o (t)]} = \sum_{m=0}^{m}{b_m \frac{d^m}{dt^m} \, [f_o(t)]}$

$\displaystyle \sum_{n=0}^{n}{a_n \, p^n f_o (t)} = \sum_{m=0}^{m}{b_m \, p^m f_o(t)}$

$\displaystyle A(p) f_o (t) = B(p) f_1 (t)$

– – – (2)

donde

$\displaystyle A(p) = a_n p^n + a_{n-1} p^{n-1} + \cdots a_1 p + a_n$ ,

$\displaystyle B(p) = b_m p^m + b_{m-1} p^{m-1} + \cdots b_1 p + b_n$

En un sistema lineal los coeficientes $a_n$ y $b_m$ son independientes de la función de respuesta. En el sistema invariante (o de parámetros constantes) los coeficientes $a_n$ y $b_n$ son constantes.

De la ecuación (2), puede expresarse simbólicamente en la forma

$\displaystyle f_o (t) - \frac{B(p)}{A(p)} f_i (t) = H(p) f_i(t)$

– – – (3)

donde $H(p) = B(p)/A(p)$ . Se entiende que la ecuación (4) es una expresión operacional de la ecuación diferencial (1). El operador $H(p)$ que opera sobre la función de entrada para producir la función de salida, se denomina operacional del sistema. Utilizando el símbolo $L$ para $H(p)$ , la ecuación (3) se puede expresar como

$\displaystyle L \left\{f_1(t) \right\} = f_o(t)$

– – – (4)

El símbolo u operador lineal $L$ en la ecuación (4) indica la ley que determina la función de salida, $f_o(t)$ , dada la función de entrada, $f_1(t)$ . A veces se menciona la ecuación (4) como una transformación $L$ de la función $f_1(t)$ en la función $f_o(t)$ .

Con la notación de (4), un sistema lineal e invariante en el tiempo está defindo por

$L \left\{a_1 {f_i}_1 (t) + a_2 {f_i}_2 (t) \right\} = a_1 L \left\{{f_i}_1 (t)\right\} + a_2 L \left\{{f_i}_2 (t) \right\}$

$\displaystyle L \left\{f_i (t + t_0) \right\} = f_o (t+t_0)$

donde $t_0$ es una constante arbitraria.

Problemas resueltos

Problema 1. Obtener la expresión operacional para la respuesta de la corriente $i(t)$ , al voltaje $v(t)$ , del circuito que se muestra en la figura 1.

Figura 6.2.1 Circuito del problema 1. — *Figura 1. Circuito del problema 1.*

Solución. La fuente es el voltaje aplicado $v(t)$ , y la respuesta es la corriente $i(t)$ , como se muestra en la figura 2.

Figura 6.2.2 Sistema del circuito del problema 1. — *Figura 2. Sistema del circuito del problema 1.*

La ecuación diferencial que relaciona $i(t)$ y $v(t)$ se puede obtener utilizando la ley de voltaje de Kirchhoff; entonces

$\displaystyle \sum{V} = 0$

$\displaystyle V_R + V_L + V_C - V = 0$

$\displaystyle V_R + V_L + V_C = V$

$\displaystyle R i(t) + L \frac{d}{dt}[i(t)] + \frac{1}{C} \int_{-\infty}^{t}{i(t) \, dt} = v(t)$

Diferenciando en ambos miembros

$\displaystyle \frac{d}{dt} \left[R i(t) + L \frac{d}{dt}[i(t)] + \frac{1}{C} \int_{-\infty}^{t}{i(t) \, dt} \right] = \frac{d}{dt}[v(t)]$

$\displaystyle \frac{d}{dt} [R i(t)] + \frac{d}{dt} \left[L \frac{d}{dt}[i(t)] \right] + \frac{d}{dt} \left[\frac{1}{C} \int_{-\infty}^{t}{i(t) \, dt} \right] = \frac{d}{dt}[v(t)]$

$\displaystyle R \frac{d}{dt} [i(t)] + L \frac{d^2}{dt^2}[i(t)] + \frac{1}{C} i(t) = \frac{d}{dt}[v(t)]$

$\displaystyle L \frac{d^2}{dt^2}[i(t)] + R \frac{d}{dt} [i(t)] + \frac{1}{C} i(t) = \frac{d}{dt}[v(t)]$

– – – – (5)

Nota. En esta última expresión, el símbolo $L$ representa la inductancia y no al operador L.

Utilizando el operador $\displaystyle p = \frac{d}{dt}$ (y también $\displaystyle p^2 = \frac{d^2}{dt^2}$ ), la ecuación (5) se expresa de la siguiente manera

$\displaystyle L p^2 i(t) + R p i(t) + \frac{1}{C} i(t) = p \,v(t)$

Factorizando

$\displaystyle \left(L p^2 + R p + \frac{1}{C} \right) i(t) = p \, v(t)$

Despejando $i(t)$

$\displaystyle i(t) = \frac{p \, v(t)}{ \left(L p^2 + R p + \frac{1}{C} \right)}$

$\displaystyle i(t) = \frac{p}{ \left(L p^2 + R p + \frac{1}{C} \right)} v(t)$

$\displaystyle i(t) = H(p) v(t)$

Donde

$\displaystyle H(p) = \frac{p}{ \left(L p^2 + R p + \frac{1}{C} \right)}$

$\displaystyle H(p) = \frac{1}{\left(Lp + R + \frac{1}{Cp} \right)}$

$\displaystyle H(p) = \frac{1}{Z(p)} = Y(p)$

En el circuito eléctrico de la figura 1, $Y(p)$ se denomina función de admitancia operacional, y $Z(p) = 1/Y(p)$ se denomina función de la impedancia operacional.

Problema 2. Considerar el sistema mecánico simple que se muestra en la figura 3. Obtener la expresión operacional $x(t)$ , que representa el desplazamiento de una masa $m$ desde su posición de equilibrio.

Fgura 6.2.3 Sistema mecánico del problema 2. — *Figura 3. Sistema mecánico del problema 2.*

Solución. La fuente es la fuerza aplicada $f(t)$ , y la respuesta es el desplazamiento $x(t)$ de la masa $m$ desde su posición de equilibrio.

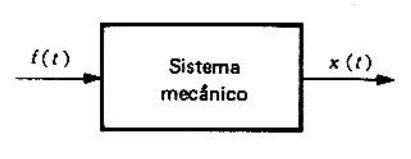
Fgura 6.2.4 Representación del sistema mecánico del problema 2. — *Figura 4. Representación del sistema mecánico del problema 2.*

Las fuerzas que acúan sobre la masa son:

la fuerza aplicada $f(t)$ ;
la reacción por inercia $\displaystyle \left(-m \frac{d^2x}{dt^2}\right)$ ;
la fuerza de amortiguamiento (resistencia por fricción) $\displaystyle \left(-k_d \frac{dx}{dt} \right)$ , y
la fuerza restauradora elástica $(-k_s x)$ .