Respuesta a funciones exponenciales de entrada – funciones propias y funciones del sistema. Fourier.

Respuesta de un sistema lineal e invariable a una función exponencial

La respuesta de un sistema lineal e invariable a una función exponencial $e^{j \omega t}$ , también es una función exponencial y proporcional a la entrada; es decir,

$L \left\{e^{j\omega t} \right\} = k e^{j\omega t}$

Demostración.

Primera interpretación. Sea $f_o (t)$ la respuesta a $e^{j\omega t}$ . Entonces,

$L \left\{e^{j\omega t} \right\} = f_o (t)$

Como el sistema es invariante, se tiene que

$L \left\{e^{j\omega (t + t_0)} \right\} = f_o (t + t_0)$

Además

$L \left\{e^{j\omega (t + t_0)} \right\} = L \left\{e^{j\omega t} e^{j\omega t_0} \right\} = e^{j\omega t_0} L \left\{e^{j\omega t} \right\} = e^{j\omega t_0} f_o(t)$

Así que

$L \left\{e^{j\omega (t + t_0)} \right\} = f_o (t + t_0)$

$e^{j\omega t_0} f_o(t) = f_o (t + t_0)$

Haciendo $t=0$ , se obtiene lo siguiente

$e^{j\omega t_0} f_o (0) = f_o (0 + t_0)$

$e^{j\omega t_0} f_o (0) = f_o (t_0)$

Como $t_0$ es arbitrario, se puede cambiar $t_0$ por $t$ y esta última expresión se muestra de la siguiente manera

$e^{j\omega t} f_o (0) = f_o (t)$

$f_o (t) = e^{j\omega t} f_o (0)$

$f_o (t) = f_o (0) e^{j\omega t}$

$f_o (t) = k \, e^{j\omega t}$

Esto quiere decir que la salida es proporcional a la entrada, siendo $k=f_o(0)$ la constante de proporcionalidad. En general, $k$ es compleja y depende de $\omega$ .

Segunda interpretación. Suponiendo que la excitación de la ecuación

$A(p) f_o(t) = B(p) f_i (t)$

es la función $f_i(t) = e^{j \omega t}$ ; entonces

$A(p) f_o(t) = B(p) e^{j \omega t}$

donde $f_o (t)$ es la respuesta del sistema. Ahora bien,

$B(p) = b_m p^m + b_{m-1} p^{m-1} + \cdots + b_1 p + b_0$ ,

$B(p) e^{j \omega t} = B(j\omega) e^{j \omega t}$

dado que

$\displaystyle p^m e^{j \omega t} = \frac{d^m}{dt^m} (e^{j \omega t}) = (j \omega)^m e^{j \omega t}$

Por tanto, la respuesta $f_o (t)$ está definida por la ecuación diferencial lineal

$\displaystyle A(p) f_o (t) = B(j\omega) e^{j \omega t}$

La función excitadora de esta última ecuación es $B(j\omega) e^{j \omega t}$ , una función exponencial, y según la teoría de ecuaciones diferenciales, se puede suponer que la respuesta $f_o (t)$ también es exponencial. De donde, si $f_o (t) = k_1 e^{j \omega t}$ , entonces

$A(p) f_o(t) = A(p) [k_1 e^{j \omega t}] = k_1 A(p) [e^{j \omega t}] = k_1 A(j\omega) e^{j \omega t} = A(j\omega) f_o (t)$

Sustituyendo, resulta lo siguiente

$\displaystyle A(p) f_o (t) = B(j\omega) e^{j \omega t}$

$\displaystyle A(j \omega) f_o (t) = B(j\omega) e^{j \omega t}$

Si $A(j \omega) \ne 0$

$\displaystyle f_o (t) = \frac{B(j \omega)}{A(j \omega)} e^{j \omega t} = H(j\omega) e^{j \omega t}$

La figura muestra un diagrama que ilustra la relación entre la entrada y la salida, dada por esta ecuación última obtenida.

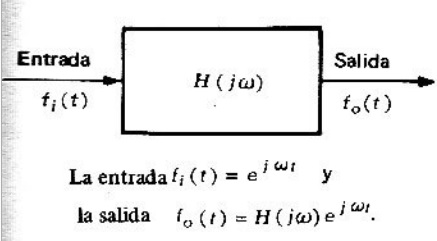
Figura 6.3.1 Función del sistema — *Figura 1. Función del sistema.*

La ecuación calculada se puede expresar en forma simbólica como

$\displaystyle L \left\{e^{j \omega t} \right\} = H(j \omega) e^{j \omega t}$

– – – (1)

En lenguaje matemático, una función $f(t)$ que satisface la siguiente ecuación

$\displaystyle L \left\{f(t) \right\} = k \, f(t)$

– – – (2)

se denomina función propia (o función característica) y el valor correspondiente de $k$ , valor propio (o valor característico). Según la ecuación (1), se puede decir que la función característica de un sistema lineal e invariante es una función exponencial. El valor propio $H(j \omega)$ del sistema está definido como la función del sistema.

Si se deseara hallar la respuesta del sistema especificado por $H(j\omega)$ , a una constante $K$ , solo se toma la ecuación (1) y la linealidad del sistema, se tiene lo siguiente

$L \left\{K \right\} = K \, H(0)$

donde

$\displaystyle H(0) = \left. H(j\omega) \right|_{\omega = 0}$

Determinando la respuesta de un sistema lineal, cuando la función de entrada es una función periódica

Si la función de entrada de un sistema lineal especificado por $H(j\omega)$ es una función periódica, con período $T$ , ¿cómo será su respuesta?

Se sabe que la función de entrada $f_i (t)$ es periódica

$\displaystyle f_i (t) = \sum_{n=-\infty}^{\infty}{c_n e^{jn\omega_0 t}}$ , $\displaystyle \omega_0 = \frac{2\pi}{T}$

donde

$\displaystyle c_n = \frac{1}{T} \int_{-T/2}^{T/2}{f_i (t) e^{-jn\omega_0 t} \, dt}$

Después

$f_{on} (t) = H(jn\omega_0) \, c_n \, e^{j n \omega_0 t}$

es la salida en respuesta a la componente de entrada

$\displaystyle f_{in} (t) = c_n \, e^{jn\omega_0 t}$

Como el sistema lineal, su respuesta total a $f_i (t)$ es la suma de las componentes $f_{on} (t)$ . De este modo

$\displaystyle \therefore f_o (t) = \sum_{n=-\infty}^{\infty}{c_n \, H(j n \omega_0) \, e^{j n \omega_0 t}}$

– – – (3)

La ecuación (3) indica que si la entrada a un sistema lineal es periódica, entonces la salida también es periódica. Se debe observar que la expresión (3) es la respuesta en estado estacionario.

Respuesta a funciones exponenciales de entrada – funciones propias y funciones del sistema. Fourier.

Respuesta de un sistema lineal e invariable a una función exponencial

Determinando la respuesta de un sistema lineal, cuando la función de entrada es una función periódica

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta

Respuesta a funciones exponenciales de entrada – funciones propias y funciones del sistema. Fourier.

Respuesta de un sistema lineal e invariable a una función exponencial

Determinando la respuesta de un sistema lineal, cuando la función de entrada es una función periódica

Comparte esto:

Relacionado

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta