Aplicaciones a circuitos eléctricos. Fourier.

Problemas resueltos

Problema 1. Una fuente de voltaje $v(t) = v_m \cos{(\omega t + \beta)}$ se aplica al circuito en serie RLC, que se muestra en la figura 1. Hallar la corriente de respuesta $i_s (t)$ en estado estacionario.

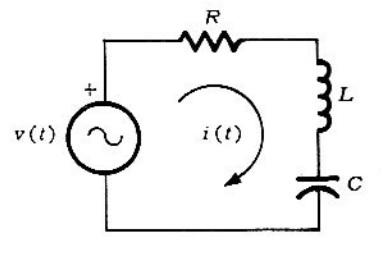
Figura 6.5.1 Circuito en serie RLC del problema 1. — *Figura 1. Circuito en serie RLC del problema 1.*

Solución. La ecuación diferencial que relaciona $i(t)$ y $v(t)$ se puede obtener utilizando la ley de voltaje de Kirchhoff; entonces

$\displaystyle \sum{V} = 0$

$\displaystyle V_R + V_L + V_C - V = 0$

$\displaystyle V_R + V_L + V_C = V$

$\displaystyle R i(t) + L \frac{d}{dt}[i(t)] + \frac{1}{C} \int_{-\infty}^{t}{i(t) \, dt} = v(t)$

Diferenciando en ambos miembros

$\displaystyle \frac{d}{dt} \left[R i(t) + L \frac{d}{dt}[i(t)] + \frac{1}{C} \int_{-\infty}^{t}{i(t) \, dt} \right] = \frac{d}{dt}[v(t)]$

$\displaystyle \frac{d}{dt} [R i(t)] + \frac{d}{dt} \left[L \frac{d}{dt}[i(t)] \right] + \frac{d}{dt} \left[\frac{1}{C} \int_{-\infty}^{t}{i(t) \, dt} \right] = \frac{d}{dt}[v(t)]$

$\displaystyle R \frac{d}{dt} [i(t)] + L \frac{d^2}{dt^2}[i(t)] + \frac{1}{C} i(t) = \frac{d}{dt}[v(t)]$

$\displaystyle L \frac{d^2}{dt^2}[i(t)] + R \frac{d}{dt} [i(t)] + \frac{1}{C} i(t) = \frac{d}{dt}[v(t)]$

Utilizando el operador $\displaystyle p = \frac{d}{dt}$ (y también $\displaystyle p^2 = \frac{d^2}{dt^2}$ ), la ecuación (5) se expresa de la siguiente manera

$\displaystyle L p^2 i(t) + R p i(t) + \frac{1}{C} i(t) = p \,v(t)$

Factorizando

$\displaystyle \left(L p^2 + R p + \frac{1}{C} \right) i(t) = p \, v(t)$

Despejando $i(t)$

$\displaystyle i(t) = \frac{p \, v(t)}{ \left(L p^2 + R p + \frac{1}{C} \right)}$

$\displaystyle i(t) = \frac{p}{ \left(L p^2 + R p + \frac{1}{C} \right)} \ v(t)$

$\displaystyle i(t) = H(p) \ v(t)$

Donde

$\displaystyle H(p) = \frac{p}{ \left(L p^2 + R p + \frac{1}{C} \right)}$

$\displaystyle H(p) = \frac{1}{\left(Lp + R + \frac{1}{Cp} \right)}$

$\displaystyle H(p) = \frac{1}{Z(p)} = Y(p)$

Utilizando la notación fasorial, se tiene que

$v(t) = v_m \cos{(\omega t + \beta)} = \text{Re} [\mathbf{V}_m \ e^{j \omega t}]$

donde $\mathbf{V}_m = v_m e^{j \beta}$ .

Entonces, la respuesta senuoidal en estado estacionario $i_s (t)$ , está dada por

$\displaystyle i_s (t) = \text{Re} \left[\frac{1}{Z(j \omega)} \mathbf{V}_m e^{j \omega t} \right]$

Después

$\displaystyle Z(j\omega) = R + j\omega L + \frac{1}{j \omega C}$

$\displaystyle Z(j\omega) = R + j \left(\omega L - \frac{1}{\omega C} \right) = |Z(j \omega)| e^{j \theta(\omega)}$

$\displaystyle Z(j\omega) = |Z(j\omega)| \measuredangle \theta(\omega)$

donde

$\displaystyle |Z (j\omega)| = \sqrt{R^2 + \left(\omega L - \frac{1}{\omega C} \right)^2}$

$\displaystyle \theta (\omega) = \tan^{-1} \left(\frac{\omega L - \frac{1}{\omega C}}{R} \right)$

Finalmente

$\displaystyle \therefore i_s (t) = \frac{v_m}{|Z(j \omega)|} \cos{[\omega t + \beta - \theta(\omega)]}$

Mediante la notación fasorial, la ecuación

$\displaystyle i_s (t) = \text{Re} \left[\frac{1}{Z(j \omega)} \mathbf{V}_m e^{j \omega t} \right]$

se puede expresar como

$\displaystyle i_s (t) = \text{Re} [\mathbf{I}_m e^{j \omega t}]$

Entonces, el fasor $\mathbf{I}_m$ , que representa a $i_s (t)$ , está relacionado con el fasor $\mathbf{V}_m$ , que representa a $v(t)$ , por

$\displaystyle \mathbf{I}_m = \frac{1}{Z(j \omega)} \mathbf{V}_m = Y(j \omega) \mathbf{V}_m$

o también,

$\displaystyle \frac{\mathbf{V}_m}{\mathbf{I}_m} = Z(j \omega)$

$\displaystyle \frac{\mathbf{I}_m}{\mathbf{V}_m} = Y(j \omega)$

donde $Z(j \omega)$ y $Y(j \omega)$ se denominan funciones senusoidales de impedancia y admitancia del circuito, respectivamente.

Problema 2. Una fuente de voltaje $v(t)$ , cuya forma es una onda cuadrada, como se observa en la siguiente figura 2, se aplica al circuito en serie RL que se muestra en la figura 3. Hallar la respuesta $i_s (t)$ , en estado estacionario.

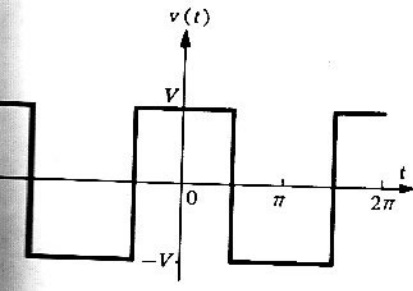
Figura 6.5.2 Forma de onda de la fuente de voltaje del problema 2. — *Figura 2. Forma de onda de la fuente de voltaje del problema 2.*

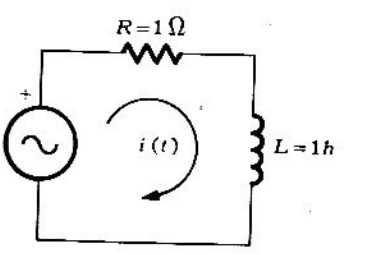
Figura 6.5.3 Circuito en serie RL del problema 2. — *Figura 3. Circuito en serie RL del problema 2.*

Solución. Primero se determinar la expansión en serie de Fourier de la onda cuadrada. Se observa que

$v(-t) = v(t)$ y $\displaystyle v \left(t + \frac{1}{2} T \right) = - v(t)$

Y esto quiere decir que la función $v(t)$ tiene simetría de cuarto de onda par. Por lo que, la serie de Fourier esperado es

$v(t) = \displaystyle \sum_{n=1}^{\infty}{a_{2n-1} \cos{(2n-1) \omega_0 t}}$

Calculando $a_{2n-1}$

$\displaystyle a_{2n-1} = \frac{8}{T} \int_{0}^{T/4}{v(t) \cos{(2n-1) \omega_0 t} \, dt}$

$\displaystyle a_{2n-1} = \frac{8}{T} \int_{0}^{T/4}{(V) \cdot \cos{(2n-1) \omega_0 t} \, dt}$

$\displaystyle a_{2n-1} = \frac{8V}{T} \int_{0}^{T/4}{\cos{(2n-1) \omega_0 t} \, dt}$

$\displaystyle a_{2n-1} = \frac{8V}{T} \left[ \frac{1}{(2n-1) \omega_0} \sin{(2n-1) \omega_0 t} + C \right]_{0}^{T/4}$

$\displaystyle a_{2n-1} = \frac{8V}{T} \left[ \frac{1}{(2n-1) \omega_0} \sin{(2n-1) \omega_0 (\frac{T}{2})} - \frac{1}{(2n-1) \omega_0} \sin{(2n-1) \omega_0 (0)} \right]$

$\displaystyle a_{2n-1} = \frac{8V}{T} \left[ \frac{1}{(2n-1) \omega_0} \sin{(2n-1) (\frac{2\pi}{T}) (\frac{T}{4})} - \frac{1}{(2n-1) \omega_0} \sin{(0)} \right]$

$\displaystyle a_{2n-1} = \frac{8V}{T} \left[ \frac{1}{(2n-1) \omega_0} \sin{(2n-1) \frac{\pi}{2}} \right] = \frac{8}{T} \left[ \frac{1}{(2n-1) \frac{2\pi}{T}} \sin{(2n-1) \frac{\pi}{2}} \right]$

$\displaystyle a_{2n-1} = \frac{8V}{T} \left[ \frac{T}{2 (2n-1) \pi} \sin{(2n-1) \frac{\pi}{2}} \right] = \frac{4}{(2n-1) \pi} \sin{(2n-1) \frac{\pi}{2}}$

Si $n=1,3,5, \cdots$

$\displaystyle a_{2n-1} = \frac{4V}{(2n-1) \pi} \sin{(2n-1) \frac{\pi}{2}}$

$\displaystyle a_{2n-1} = \frac{4V}{(2n-1) \pi} (1) = \frac{4V}{(2n-1) \pi}$

$\displaystyle a_{2n-1} = \frac{4V}{(2n-1) \pi}$

Si $n=2,4,6, \cdots$

$\displaystyle a_{2n-1} = \frac{4V}{(2n-1) \pi} \sin{(2n-1) \frac{\pi}{2}}$

$\displaystyle a_{2n-1} = \frac{4V}{(2n-1) \pi} (-1) = - \frac{4V}{(2n-1) \pi}$

$\displaystyle a_{2n-1} = - \frac{4V}{(2n-1) \pi}$

Entonces $a_{2n-1}$ es

$\displaystyle \large a_{2n-1} = \left\{ \begin{matrix} \frac{4V}{(2n-1) \pi} & , & n=1,3,5, \cdots \\ - \frac{4V}{(2n-1) \pi} & , & n =2,4,6, \cdots \end{matrix} \right.$

Regresando, la expansión de la serie de Fourier para la forma de onda de la figura 2 es

$\displaystyle v(t) = \sum_{n=1}^{\infty}{a_{2n-1} \cos{(2n-1) \omega_0 t}}$

$\displaystyle v(t) = \sum_{n=1}^{\infty}{\frac{4V}{(2n-1) \pi} \sin{(2n-1) \frac{\pi}{2}} \cdot \cos{(2n-1) \omega_0 t}}$

$\displaystyle v(t) = \frac{4V}{\pi} \sum_{n=1}^{\infty}{\left(\frac{1}{2n-1} \right) \sin{(2n-1) \frac{\pi}{2}} \cdot \cos{(2n-1) \omega_0 t}}$

$\displaystyle v(t) = \frac{4V}{\pi} \left(\cos{\omega_0 t} - \frac{1}{3} \cos{3 \omega_0 t} + \frac{1}{5} \cos{5 \omega_0 t} - \cdots \right)$

Como $T=2\pi$ , $\displaystyle \omega_0 = \frac{2\pi}{T} = \frac{2\pi}{2\pi} = 1$ , por lo que

$\displaystyle v(t) = \frac{4V}{\pi} \left(\cos{t} - \frac{1}{3} \cos{3t} + \frac{1}{5} \cos{5t} - \cdots \right)$

La impedancia del circuito RL (figura 3) a cualquier frecuencia angular $\omega$ está dada por

$Z(j \omega) = R + j\omega L$

Por consiguiente, para el armónico enésimo la impedancia es

$\displaystyle Z(j n \omega_o) = R + jn\omega_o L$

Como el problema brinda $R=1\Omega$ y $L=1 \ H$ (sin olvidar a $\omega_0 = 1$ ), entonces

$\displaystyle Z(j n \omega_o) = 1 + jn = |Z(jn)| \measuredangle \theta(n)$

donde

$\displaystyle |Z(jn)| = \sqrt{1 + n^2}$

$\displaystyle \theta(n) = \tan^{-1}(n)$

Según el principio de superposición, se sigue que la respuesta en estado estacionario $i_s(t)$ , está dada por

$\displaystyle i_s (t) = \frac{v_m}{|Z(j n)|} \cos{[nt + \beta - \theta(n)]} = \frac{1}{|Z(j n)|} \cdot v_m \cdot \cos{[nt + \beta - \theta(n)]}$

$\displaystyle i_s (t) = v_m \cdot \frac{1}{|Z(j n)|} \cos{[nt + \beta - \theta(n)]}$

$\displaystyle i_s(t) = \frac{4V}{\pi} \left[ \frac{1}{\sqrt{1+1^2}} \cos{(t - \tan^{-1}{1})} - \frac{1}{\sqrt{1+3^2}} \ \frac{1}{3} \cos{(3t - \tan^{-1}{3})} + \frac{1}{\sqrt{1+5^2}} \ \frac{1}{5} \cos{(5t - \tan^{-1}{5})} - \cdots \right]$

Finalmente, el resultado final es

$\displaystyle \therefore i_s(t) = \frac{4V}{\pi} \left[ \frac{1}{\sqrt{2}} \cos{(t - \tan^{-1}{1})} - \frac{1}{3\sqrt{10}} \cos{(3t - \tan^{-1}{3})} + \frac{1}{5 \sqrt{26}} \cos{(5t - \tan^{-1}{5})} - \cdots \right]$

Problema 3. El voltaje de entrada al circuito RC, de dos fuentes, que se muestra en la figura 4, es la serie finita de Fourier

$\displaystyle v(t) = 100 \cos{t} + 10 \cos{3t} + \cos{5t}$

Hallar la respuesta resultante $v_{os} (t)$ en estado estacionario.

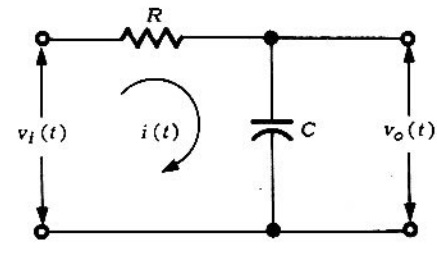
Figura 6.5.4 Circuito RC de dos fuentes. — *Figura 4. El circuito RC de dos fuentes.*

Solución. La fuente es

$\displaystyle v_i (t) = R \ i(t) + \frac{1}{C} \int_{-\infty}^{t}{i(t) \, dt}$

$\displaystyle v_i (t) = R \ i(t) + \frac{1}{C} \ \frac{1}{p} \ i(t)$

$\displaystyle v_i (t) = R \ i(t) + \frac{1}{pC} \ i (t)$

$\displaystyle v_i (t) = \left(R + \frac{1}{pC} \right) i (t)$

La respuesta es

$\displaystyle v_o (t) = \frac{1}{C} \int_{-\infty}^{t}{i(t) \, dt}$

$\displaystyle v_o (t) = \frac{1}{C} \ \frac{1}{p} i(t)$

$\displaystyle v_o (t) = \frac{1}{pC} i(t)$

Realizando la siguiente división

$\displaystyle \frac{v_o (t)}{v_i (t)} = \frac{\frac{1}{pC} i(t)}{\left(R + \frac{1}{pC} \right) i (t)}$

$\displaystyle \frac{v_o (t)}{v_i (t)} = \frac{\frac{1}{pC}}{\left(R + \frac{1}{pC} \right)} = \frac{\frac{1}{pC}}{\frac{\left(pRC + 1 \right)}{pC}}$

$\displaystyle \frac{v_o (t)}{v_i (t)} = \frac{1}{pRC + 1}$

Por consiguiente, la respuesta $v_o (t)$ y la entrada $v_i (t)$ están relacionados por

$\displaystyle \frac{v_o (t)}{v_i (t)} = \frac{1}{pRC + 1}$

$\displaystyle v_o (t) = \frac{1}{pRC + 1} v_i (t)$

$\displaystyle v_o (t) = H(p) v_i (t)$

Donde

$\displaystyle H(p) = \frac{1}{pRC + 1}$

Ahora, la razón de fasores $\mathbf{V}_o / \mathbf{V}_i$ a cualquier frecuencia angular $\omega$ es

$\displaystyle \frac{\mathbf{V}_o}{\mathbf{V}_i} = \mathbf{H}(j\omega)$

$\displaystyle \frac{\mathbf{V}_o}{\mathbf{V}_i} = \frac{1}{j \omega RC + 1} = \frac{1}{1 + j \omega RC}$

$\displaystyle \frac{\mathbf{V}_o}{\mathbf{V}_i} = \frac{1}{\sqrt{1+(\omega R C)^2}} \angle -\tan^{-1}{(\omega RC)}$

Como $\omega_o =1$ , la razón de fasores del armónico enésimo es

$\displaystyle \left. \frac{\mathbf{V}_o}{\mathbf{V}_i} \right|_n = \mathbf{H}(jn\omega_0) = \frac{1}{\sqrt{1+(\omega n R C)^2}} \angle -\tan^{-1}{(\omega n RC)}$

$\displaystyle \left. \frac{\mathbf{V}_o}{\mathbf{V}_i} \right|_n = H(jn) = \frac{1}{\sqrt{1+[(1)nR C]^2}} \angle -\tan^{-1}{[(1)nRC]}$

$\displaystyle \left. \frac{\mathbf{V}_o}{\mathbf{V}_i} \right|_n = H(jn) = \frac{1}{\sqrt{1+(nR C)^2}} \angle -\tan^{-1}{(nRC)}$

Por el principio de superposición se sigue que la respuesta en estado estacionario, $v_{os} (t)$ , está dada por

$\displaystyle v_{os} (t) = 100 \cdot \frac{1}{\sqrt{1 + (1 \cdot RC)^2}} \cos{[t -\tan^{-1}{(1 \cdot RC)}]} + 10 \cdot \frac{1}{\sqrt{1 + (3 \cdot RC)^2}} \cos{[3t - \tan^{-1}{(3 \cdot RC)}]} + \frac{1}{1 + (5 \cdot RC)^2} \cos{[5t - \tan^{-1}{(5 \cdot RC)}]}$

$\displaystyle v_{os} (t) = \frac{100}{\sqrt{1 + (RC)^2}} \cos{[t -\tan^{-1}{(RC)}]} + \frac{10}{\sqrt{1 + (3RC)^2}} \cos{[3t - \tan^{-1}{(3RC)}]} + \frac{1}{1 + (5RC)^2} \cos{[5t - \tan^{-1}{(5RC)}]}$

Finalmente

$\displaystyle \therefore v_{os} (t) = \frac{100}{\sqrt{1 + R^2 C^2}} \cos{[t -\tan^{-1}{(RC)}]} + \frac{10}{\sqrt{1 + 9R^2 C^2}} \cos{[3t - \tan^{-1}{(3RC)}]} + \frac{1}{1 + 25 R^2 C^2} \cos{[5t - \tan^{-1}{(5RC)}]}$

Cálculo de potencia en estado estacionario

El voltaje $v_{ab} (t)$ , en los terminales «a-b» del circuito de la figura 6.5.5, es periódico y está definido por la serie de Fourier

$\displaystyle v_{ab} (t) = V_o + \sum_{n=1}^{\infty}{V_o \cos{(n \omega_0 t + \beta_n)}}$

Y la corriente $i_s (t)$ , en estado estacionario que entra por el terminal «a» es

$\displaystyle i_s (t) = I_o + \sum_{n=1}^{\infty}{I_n \cos{(n \omega_o t + \alpha_n)}}$

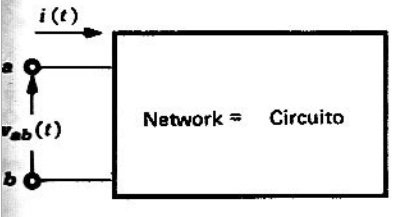
Figura 6.5.5 Circuito — *Figura 5. Circuito que contiene las terminales «a-b».*

Por lo que, la potencia promedio de entrada $P_{ab}$ está definida por

$\displaystyle P_{ab} = \frac{1}{T} \int_{-T/2}^{T/2}{v_{ab} (t) \ i_s (t) \, dt}$

Y que es igual a

$\displaystyle P_{ab} = V_o I_o + \frac{1}{2} \sum_{n=1}^{\infty}{V_n I_n \cos{(\beta_n + \alpha_n)}}$

Otra manera de expresar el resultado anterior, comienza de la siguiente manera. Denotando la raíz cuadrada media del armónico enésimo del voltaje por $V_{\text{eff},n}$ y la del armónico enésimo de la corriente por $I_{\text{eff},n}$ , se tiene

$\displaystyle \frac{1}{2} V_n I_n = V_{\text{eff},n} \ I_{\text{eff},n}$

Sea $\theta_n = \beta_n - \alpha_n$ . Entonces $\theta_n$ denota la diferencia de fase entre los armónicos enésimos del voltaje y de la corriente. Entonces

$\displaystyle P_{ab} = V_o I_o + \frac{1}{2} \sum_{n=1}^{\infty}{V_n I_n \cos{(\beta_n + \alpha_n)}}$

$\displaystyle P_{ab} = V_o I_o + \sum_{n=1}^{\infty}{\frac{1}{2} V_n I_n \cos{(\beta_n + \alpha_n)}}$

$\displaystyle P_{ab} = V_o I_o + \sum_{n=1}^{\infty}{V_{\text{eff},n} \ I_{\text{eff},n} \cos{\theta_n}}$

$\displaystyle P_{ab} = P_0 + P_1 + P_2 + \cdots$

$\displaystyle P_{ab} = \sum_{n=0}^{\infty}{P_n}$

donde $P_n$ es la potencia promedio del armónico enésimo.

Esta segunda interpretación muestra que la potencia promedio entregada por una excitación periódica a un circuito es la suma de la potencia promedio entregada por los armónicos individuales. No hay contribuciones a la potencia promedio, por parte de la corriente a una frecuencia y del voltaje a otra frecuencia.

Aplicaciones a circuitos eléctricos. Fourier.

Problemas resueltos

Cálculo de potencia en estado estacionario

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta

Aplicaciones a circuitos eléctricos. Fourier.

Problemas resueltos

Cálculo de potencia en estado estacionario

Comparte esto:

Relacionado

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta