Introducción

Se considera un sistema mecánico ilustrado por la figura 1 que contene un resorte, una masa y un amortiguador. Si ese sistema se perturba por una fuerza , el desplazamiento
, de la respuesta en estado estacionario, están determinados de la siguiente manera.
La resuesta y la función excitadora
están relacionadas por la siguiente ecuación diferencial.
donde representa la masa,
representa el coeficiente de amortiguamiento y
, la constante del resorte. La ecuación diferencial se puede expresar en forma operacional
Donde
Para encontrar el respuesta en estado estacionario, se usa la notación fasorial, por lo que resulta lo siguiente
donde . Por lo que, la respuesta en estado estacionario es
De la función , remplazando
por
, resulta que
donde
Y
Finalmente
donde se denomina ángulo de fase en retraso.
Problema resuelto
Problema 1. Analizar el movimiento en estado estacionario del sistema que se muestra en la figura 2, si la fuerza perturbadora es la que se muestra en la figura 3.
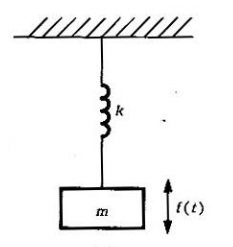
Figura 2. Sistema mecánico del problema 1. 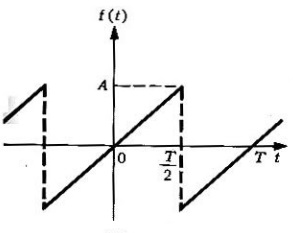
Figura 3. Fuerza perturbadora del problema 1.
Solución. La respuesta , el desplazamiento de la masa
desde su posición de equilibrio, y la fuerza perturbadora están relacionadas por
continuando
donde
La expansión en serie de Fourier de que se mostró en la figura 6.6.3 se determina de la siguiente manera. Determinando la función
, resulta
Como es una función impar, se observa que
,
Calculando el coeficiente
Si
Si
Regresando
Y la expansión esperada es
Puesto que solo interesa el movimiento forzado o el movimiento en estado estacionario del sistema, se puede utilizar la notación fasorial. Para ello,
Y
Con
°
Donde .
Finalmente, el resultado final es