Filtros ideales. Fourier.

Introducción

La siguiente ecuación muestra que en el espectro de frecuencia de la respuesta, $F_o (j\omega)$ , está relacionado con el espectro de frecuencia de la fuente, $F_i (j\omega)$ , por medio de la función del sistema, $H(j\omega)$ , según

$F_o (j\omega) = F_i (j\omega) \ H(j\omega)$

– – – – (1)

Esto se ilustra en la figura 1.

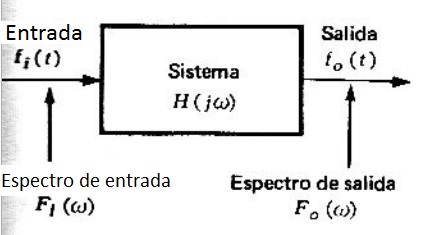
Figura 6.10.1 Ilustración de la ecuación (1)..jpg — Figura 1. Ilustración de la ecuación (1).

Se observa que $H(j\omega)$ actúa como una función ponderadora de las componentes de diferente frecuencia en la entrada. En este sentido, la relación de la ecuación (1) indica la característica de filtro del sistema lineal. Si la característica ponderadora o característica de filtro es el interés principal, entonces generalmente se hace referencia al sistema como al filtro.

El filtro ideal para frecuencias bajas se define como un sistema para el cual la función del sistema, $H(j\omega)$ , está dada por

$\displaystyle H(j\omega) = \left\{ \begin{matrix} e^{-j \omega t_0} & \mbox{para} \quad |\omega|<\omega_c \\ 0 & \mbox{para} \ \ \quad \omega>\omega_c \end{matrix} \right.$

donde a $\omega_c$ se le conoce como la frecuencia de corte.

Problema resuelto

Problema 1. Hallar $h(t)$ , la respuesta al impulso unitario, de un filtro ideal para frecuencias bajas.

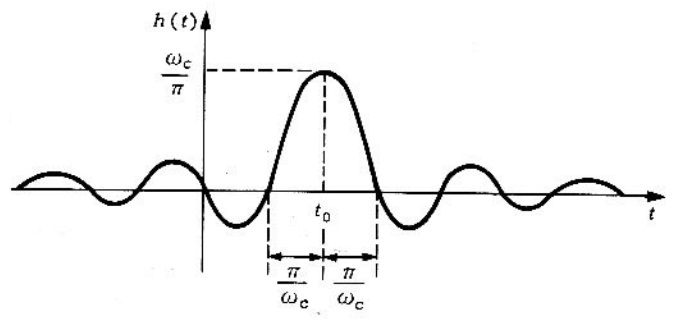
Solución. La figura 2 muestra las características de un filtro ideal para frecuencias bajas.

Figura 6.10.2 Características de frecuencia de un filtro ideal para frecuencias bajas — Figura 2. Características de la frecuencia de un filtro ideal para frecuencias bajas.

La respuesta al impulso unitario, $h(t)$ , se obtiene por

$\displaystyle h(t) = \mathcal{F}^{-1}[H(j\omega)]$

$\displaystyle h(t) = \frac{1}{2\pi} \int_{-\infty}^{\infty}{H(j\omega) \ e^{j\omega t} \, d\omega}$

$\displaystyle h(t) = \frac{1}{2\pi} \int_{-\infty}^{-\omega_c}{H(j\omega) \ e^{j\omega t} \, d\omega} + \frac{1}{2\pi} \int_{-\omega_c}^{\omega_c}{H(j\omega) \ e^{j\omega t} \, d\omega} + \frac{1}{2\pi} \int_{\omega_c}^{\infty}{H(j\omega) \ e^{j\omega t} \, d\omega}$

$\displaystyle h(t) = 0 + \frac{1}{2\pi} \int_{-\omega_c}^{\omega_c}{H(j\omega) \ e^{j\omega t} \, d\omega} + 0 = \frac{1}{2\pi} \int_{-\omega_c}^{\omega_c}{H(j\omega) \ e^{j\omega t} \, d\omega}$

$\displaystyle h(t) = \frac{1}{2\pi} \int_{-\omega_c}^{\omega_c}{e^{-j\omega t_0} \ e^{j\omega t} \, d\omega} = \frac{1}{2\pi} \int_{-\omega_c}^{\omega_c}{e^{-j\omega t_0 + j\omega t} \, d\omega}$

$\displaystyle h(t) = \frac{1}{2\pi} \int_{-\omega_c}^{\omega_c}{e^{j\omega (t - t_0)} \, d\omega} = \frac{1}{2\pi} \left[\frac{1}{j(t-t_0)} e^{j\omega (t - t_0)} + C \right]_{-\omega_c}^{\omega_c}$

$\displaystyle h(t) = \frac{1}{2\pi} \left[\frac{1}{j(t-t_0)} e^{j\omega_c (t - t_0)} - \frac{1}{j(t-t_0)} e^{-j\omega_c (t - t_0)} \right]$

$\displaystyle h(t) = \frac{1}{j2\pi(t-t_0)} \left[e^{j\omega_c (t - t_0)} -e^{-j\omega_c (t - t_0)} \right]$

$\displaystyle h(t) = \frac{1}{\pi(t-t_0)} \left[\frac{e^{j\omega_c (t - t_0)} -e^{-j\omega_c (t - t_0)}}{j2} \right]$

$\displaystyle h(t) = \frac{1}{\pi(t-t_0)} \sin{\omega_c (t-t_0)} = \frac{\omega_c}{\omega_c} \cdot \frac{1}{\pi(t-t_0)} \sin{\omega_c (t-t_0)}$

$\displaystyle h(t) = \frac{\omega_c}{\pi(t-t_0)} \ \frac{\sin{\omega_c (t-t_0)}}{\omega_c}$

$\displaystyle \therefore h(t) = \frac{\omega_c}{\pi} \ \frac{\sin{\omega_c (t-t_0)}}{\omega_c (t-t_0)}$

Este resultado se puede graficar. Esto se observa en la figura 3, de la cual se dan las siguientes conclusiones:

La entrada aplicada es distorsionada por el sistema, debido al hecho de que el filtro transmite sólo una limitada banda de frecuencias.
El valor pico de la respuesta $\omega_c / \pi$ es proporcional a la frecuencia de corte $\omega_c$ . El ancho del pulso principal es $2\pi / \omega_c$ ; se puede hacer referencia a esta cantidad, como la duración efectiva del pulso de salida, $T_d$ . Se observa que cuando $\omega_c \rightarrow \infty$ (es decir, cuando el filtro permite el paso de todas las frecuencias), $T_d \rightarrow 0$ , y el pico de la respuesta $\rightarrow \infty$ ; en otros términos la respuesta se aproxima a un impulso, tal como debe ser.
También se observa que la respuesta no es cero antes de $t=0$ , es decir, antes de se aplique la entrada. Esta es la característica de un sistema físicamente no realizable. Los filtros ideales no son físicamente realizables, y por consiguiente, no son necesariamente sistemas casuales.

Figura 6.10.3 La respuesta al impulso unitario de un filtro ideal para frecuencias bajas — Figura 3. La respuesta al impulso unitario de un filtro ideal para frecuencias bajas.

Función seno – integral

La función seno – integral (del límite superior $y$ ) es

$\displaystyle Si (y) = \int_{0}^{y}{\frac{\sin{x}}{x} \, dx} = \int_{0}^{y}{Sa (x) \, dx}$

Problema resuelto

Problema 2.

(a) Evaluar la función seno-integral.
(b) Hallar $a(t)$ , la respuesta al escalón unitario de un filtro ideal para frecuencias.

Solución (a). Dado que $\displaystyle Sa(x) = \frac{\sin{x}}{x}$ es una función par, entonces

$\displaystyle Si (-y) = - Si (y)$

Según la definición, cuando $y=0$ , entonces

$\displaystyle Si (0) = 0$

Dado que

$\displaystyle \int_{-\infty}^{\infty}{\frac{\sin{x}}{x} \, dx} = 2 \int_{0}^{\infty}{\frac{\sin{x}}{x} \, dx} = \pi$

Entonces, si

$\displaystyle Si (y) = \int_{0}^{y}{\frac{\sin{x}}{x} \, dx}$

Cuando $y=\infty$ , resulta que

$\displaystyle Si (\infty) = \int_{0}^{\infty}{\frac{\sin{x}}{x} \, dx} = \frac{\pi}{2}$

Y cuando $y=-\infty$ , resulta que

$\displaystyle Si (-\infty) = \int_{0}^{-\infty}{\frac{\sin{x}}{x} \, dx} = - \int_{-\infty}^{0}{\frac{\sin{x}}{x} \, dx} = - \frac{\pi}{2}$

En la figura 4 se muestra una gráfica de $Si(y)$ .

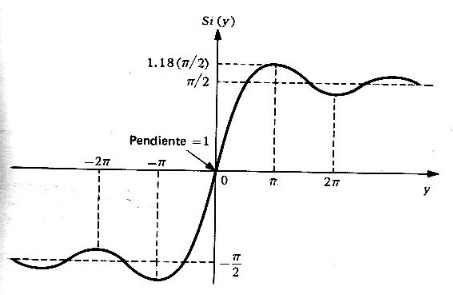
Figura 6.10.4 Función seno-integral — Figura 4. Función seno – integral.

Solución (b). Recordando que la respuesta al impulso unitario, de un filtro ideal para frecuencias bajas fue de

$\displaystyle h(t) = \frac{\omega_c}{\pi} \ \frac{\sin{\omega_c (t-t_0)}}{\omega_c (t-t_0)}$

lo cual, cambiando la variable $t$ por $\tau$ , se tiene

$\displaystyle h(\tau) = \frac{\omega_c}{\pi} \ \frac{\sin{\omega_c (\tau-t_0)}}{\omega_c (\tau-t_0)}$

La respuesta al escalón unitario, se puede obtener de $h(t)$ , la respuesta al impulso unitario; es decir,

$\displaystyle a(t) = \int_{-\infty}^{t}{h(\tau) \, d\tau}$

$\displaystyle a(t) = \int_{-\infty}^{t}{\frac{\omega_c}{\pi} \ \frac{\sin{\omega_c (\tau-t_0)}}{\omega_c (\tau-t_0)} \, d\tau} = \int_{-\infty}^{t}{\frac{1}{\pi} \ \frac{\sin{\omega_c (\tau-t_0)}}{(\tau-t_0)} \, d\tau}$

$\displaystyle a(t) = \frac{1}{\pi} \int_{-\infty}^{t}{\frac{\sin{\omega_c (\tau-t_0)}}{(\tau-t_0)} \, d\tau}$

Remplazando la variable $\omega_0 (t - t_0)$ por $x$

$\displaystyle a(t) = \frac{1}{\pi} \int_{-\infty}^{t}{\frac{\sin{\omega_c (\tau-t_0)}}{(\tau-t_0)} \, d\tau} = \frac{1}{\pi} \int_{-\infty}^{\omega_c (t - t_0)}{\frac{\sin{x}}{x} \, dx}$

$\displaystyle a(t) = \frac{1}{\pi} \int_{-\infty}^{0}{\frac{\sin{x}}{x} \, dx} + \frac{1}{\pi} \int_{0}^{\omega_c (t - t_0)}{\frac{\sin{x}}{x} \, dx}$

$\displaystyle a(t) = \frac{1}{\pi} \int_{0}^{\infty}{\frac{\sin{x}}{x} \, dx} + \frac{1}{\pi} \int_{0}^{\omega_c (t - t_0)}{\frac{\sin{x}}{x} \, dx}$

Mediante la función seno-integral, la ecuación se puede expresar como

$\displaystyle a(t) = \frac{1}{\pi} \int_{0}^{\infty}{\frac{\sin{x}}{x} \, dx} + \frac{1}{\pi} \int_{0}^{\omega_c (t - t_0)}{\frac{\sin{x}}{x} \, dx}$

$\displaystyle a(t) = \frac{1}{\pi} \cdot \frac{\pi}{2} + \frac{1}{\pi} \cdot \text{Si} \left[ \omega_c (t - t_0) \right]$

$\displaystyle \therefore a(t) = \frac{1}{2} + \frac{1}{\pi} \text{Si} \left[ \omega_c (t - t_0) \right]$

En la figura 5 se muestra la gráfica de $a(t)$ , la respuesta al escalón unitario.

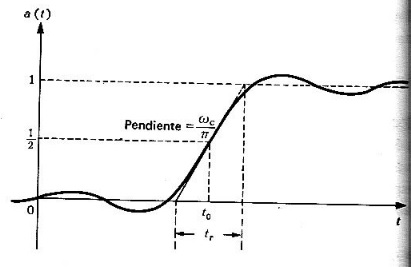
Figura 6.10.5 Respuesta al escalón unitario de un filtro ideal para frecuencias bajas — Figura 5. Respuesta al escalón unitario de un filtro ideal para frecuencias bajas.

En el resultado anterior se observa lo siguiente:

se observa nuevamente la distorsión debida a la banda limitada del filtro;
se observa nuevamente que la respuesta no es cero antes de $t=0$ ;
utilizando $\displaystyle \text{Si} (\pm \infty) = \pm \frac{\pi}{2}$ , se observa que cuando $\omega_c \rightarrow \infty$ ,

$\displaystyle a(t) = \frac{1}{2} + \frac{1}{\pi} \text{Si} \left[ \omega_c (t - t_0) \right] = \frac{1}{2} - \frac{1}{2} =0 \quad \mbox{para} \quad t<t_0$

$\displaystyle a(t) = \frac{1}{2} + \frac{1}{\pi} \text{Si} \left[ \omega_c (t - t_0) \right] = \frac{1}{2} + \frac{1}{2} = 1 \quad \mbox{para} \quad t>t_0$

y la respuesta se convierte en $u(t-t_0)$ , un escalón unitario retardado, tal como debe de ser, y

4. la entrada, un escalón unitario, tiene un súbito ascenso mientras la respuesta muestra un ascenso gradual.

Si se define el tiempo de ascenso de la respuesta $a(t)$ , como al intervalo $t_r$ entre las intercepciones de la tangente en $r=t_0$ , con las líneas $a(t) = 0$ y $a(\infty) = 1$ , entonces, como es evidente según en la figura 5, se tiene

$\displaystyle \left. \frac{d}{dt}[a(t)] \right|_{t=t_0} = \frac{1}{t_r} = \frac{\omega_c}{\pi}$

– – – – (2)

Por tanto,

$\displaystyle t_r = \frac{\pi}{\omega_c}$

– – – – (3)

$\displaystyle \omega_c t_r = \pi$

– – – – (4)

El tiempo de ascenso (o tiempo de súbida) $t_r$ está dado por la ecuación (3) y es inversamente proporcional al ancho de banda del filtro. La ecuación (4) indica que

$(\mbox{ancho de banda}) \times (\mbox{tiempo de ascenso}) = \mbox{constante}$

Filtros ideales. Fourier.

Introducción

Problema resuelto

Función seno – integral

Problema resuelto

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta

Filtros ideales. Fourier.

Introducción

Problema resuelto

Función seno – integral

Problema resuelto

Comparte esto:

Relacionado

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta