Circuitos magnéticos. Problema 5. Máquinas eléctricas.

Problema 5.

El núcleo que se muestra en la figura 1.1.9 es de acero, con una curva de magnetización que se muestra en la figura 1.1.10. Las corrientes $i_1$ e $i_2$ son de 0.5 A y 1 A respectivamente. Si $\mu_r$ no es constante, ¿cuánto flujo producen en el núcleo las corrientes especificadas? ¿Cuál es la permeabilidad de éste núcleo en éstas condiciones? La permeabilidad relativa es de 1200, ¿es buena suposición para estas condiciones? ¿Es una buena suposición en general?

Figura 1.1.9 Núcleo de acero.

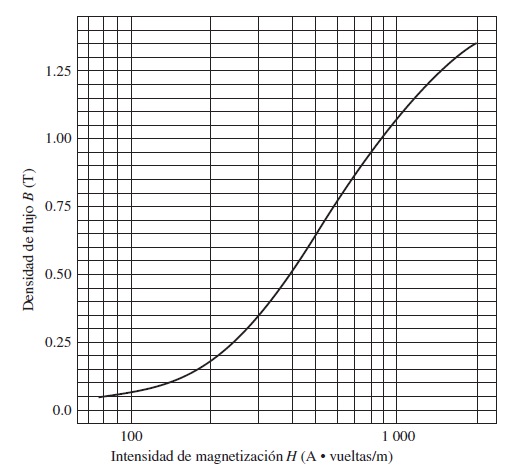
Figura 1.1.10 Curva de magnetización perteneciente al núcleo de acero.

Solución.

Primero se determina la fuerza magnetomotriz total. De acuerdo con la descripción de la figura 1.1.9, $N_1 = 600$ espiras y $N_2 = 200$ espiras, y del enunciado del problema, $i_1 = 0.5 \ A$ y $i_2 = 1 \ A$ . Entonces

$\mathcal{F} = N_1 \ i_1 + N_2 \ i_2$

$\mathcal{F} = (600 \ espiras)(0.5 \ A) + (200 \ espiras)(1 \ A)$

$\mathcal{F} = 500 \ A \cdot espiras$

Después, se determina el área de la sección transversal.

$A = (0.15 \ m)(0.15 \ m)$

$A = 0.0225 \ m^2$

Luego, se calcula la longitud total del núcleo. Se tomará completo debido a que las dimensiones del núcleo son iguales de lado y lado. Se debe recordar que la longitud debe estar expresada en metros.

$l = 7.5 + 50 + 7.5 + 7.5 + 50 + 7.5 + 7.5 + 50 + 7.5 + 7.5 + 50 + 7.5$

$l = 260 \ cm$

$l = 2.6 \ m$

Para saber el valor de la intensidad de magnetización, se despeja la variable $H$ a partir de esta fórmula

$\mathcal{F} = H \ l$

$\displaystyle H = \frac{\mathcal{F}}{l}$

$\displaystyle H = \frac{500 \ A \cdot espiras}{2.6 \ m}$

$H = 192.31 \ (A \cdot espiras / m)$

Estudiando la curva de magnetización de la figura 1.1.10 con el valor de la intensidad de magnetización (ver figura 1.1.11)

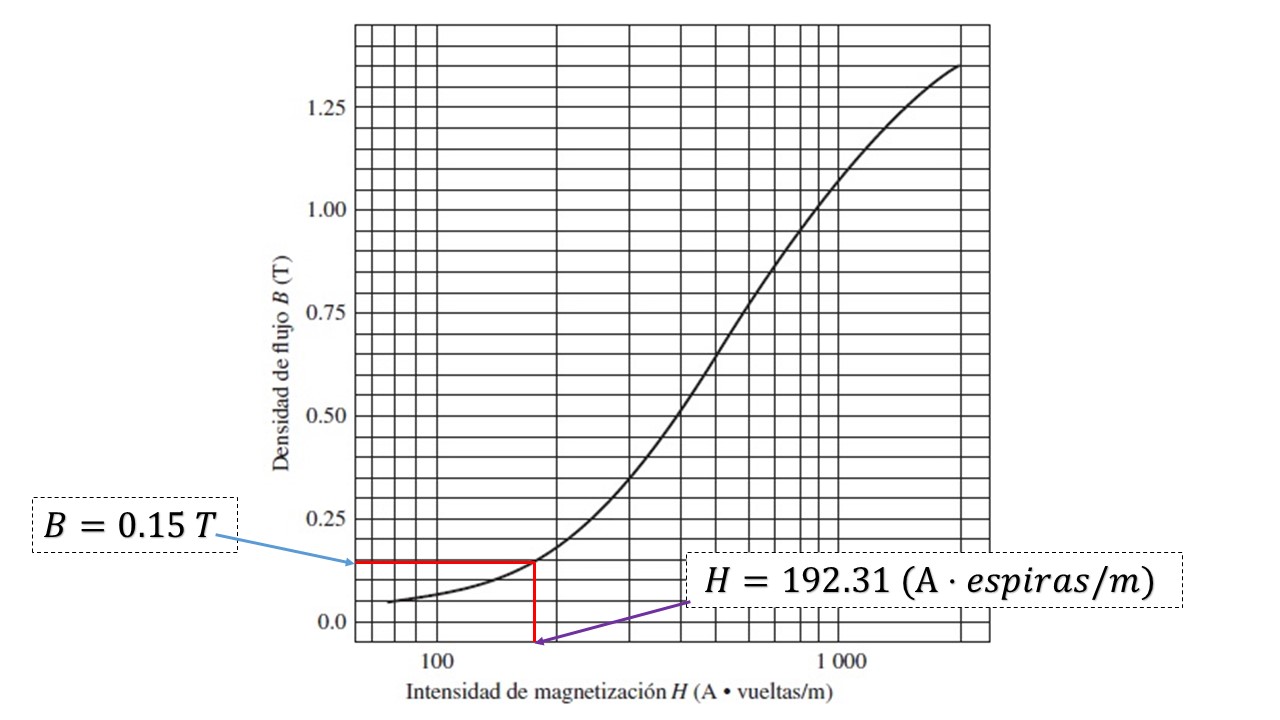
Figura 1.1.11 Ubicación del valor de la densidad magnética por medio de la curva de magnetización.

El valor de la densidad magnética es

$B=0.15 \ T$

Calculando el flujo que produce el núcleo

$\phi = B \ A$

$\phi = (0.15 \ T)(0.0225 \ m^2)$

$\phi = 0.0034 \ Wb$

$\phi = 3.4 \times 10^{-3} \ Wb = 3.4 \ mWb$

Finalmente, de calcula la permeabilidad relativa partiendo de la siguiente fórmula. Posteriormente, se despeja la variable perteneciente a la fuerza magnetomotriz

$\mathcal{F} = \phi \ \mathcal{R}$

$\displaystyle \mathcal{R} = \frac{\mathcal{F}}{\phi}$

$\displaystyle \frac{\mathcal{F}}{\phi} = \frac{N \ i}{B \ A} = \frac{N \ i}{\mu \ H \ A} = \frac{N \ i}{\mu \ \frac{N \ i}{l_n} \ A}$

$\displaystyle \frac{\mathcal{F}}{\phi} = \frac{l_n}{\mu \ A}$

$\displaystyle \frac{\mathcal{F}}{\phi} = \frac{l_n}{\mu_0 \ \mu_r \ A}$

$\displaystyle \mu_r = \frac{\phi \ l_n}{\mu_0 \ A \ \mathcal{F}}$

$\displaystyle \mu_r = \frac{(3.4 \times 10^{-3} \ Wb)(2.6 \ m)}{(4\pi \times 10^{-7} H/m)(0.0225 \ m^2)(500 \ A \cdot espiras)}$

$\mu_r \approx 625.3$

Contestando las preguntas mencionadas en el enunciado del problema

No es buena suposición de que $\mu_r$ no sea constante.
No es buena suposición en general
El flujo que produce en el núcleo con las corrientes especificadas es de 3.4 m Wb ( $3.4 \times 10^{-3} \ Wb$ )
La permeabilidad de este núcleo es de 625.3, aproximadamente.

Circuitos magnéticos. Problema 5. Máquinas eléctricas.

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta

Circuitos magnéticos. Problema 5. Máquinas eléctricas.

Comparte esto:

Relacionado

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta