Circuitos magnéticos. Problema 9. Máquinas eléctricas.

Problema 9.

La figura 1.1.24 muestra el núcleo de un motor de cd sencillo. La curva de magnetización del metal de este núcleo está dada por las figuras 1.1.25 y 1.1.26. Suponga que el área de la sección transversal de cada entrehierro es de 18 $cm^2$ y que el ancho de cada entrehierro es de 0.05 (cm). El diámetro efectivo del núcleo del rotor es de 5 (cm).

a) Se desea construir una máquina con la mayor densidad posible de flujo posible, pero evitando la excesiva saturación en el núcleo. ¿Cuál sería un máximo razonable de densidad de flujo para éste núcleo?

b) ¿Cuál sería el flujo total en el núcleo para la densidad de flujo del inciso a)?

c) La máxima corriente de campo posible de esta máquina es de 1 A. Seleccione un número razonable posible de vueltas de alambre para proveer la densidad de flujo requerida sin exceder la máxima corriente disponible.

Figura 1.1.24 Núcleo de un motor de cd sencillo

Figura 1.1.25 Curva de magnetización del núcleo

Figura 1.1.26 Curva de magnetización del núcleo.

Solución.

Se realiza una conversión en el valor del área de la sección transversal de centímetros a metros cuadrados de cada entrehierro. Para el entrehierro de a columna izquierda

$A_1 = 18 \ cm^2$

$\displaystyle A_1 = 18 \ cm^2 \left(\frac{1 \ m}{100 \ cm} \right)^2$

$0.0018 \ m^2$

Y para el entrehierro de la columna derecha

$A_2 = 18 \ cm^2$

$A_2 = 0.0018 \ m^2$

El área de la sección transversal del núcleo es

$A = (0.05 \ m)(0.05 \ m)$

$A = 0.0025 \ m^2$

El área del estator es

$A_{estator} = (0.05 \ m)(0.05 \ m)$

$A_{estator} = 0.0025 \ m^2$

El área del rotor es

$A_{rotor} = (0.05 \ m)(0.05 \ m)$

$A_{rotor} = 0.0025 \ m^2$

Después, se realiza una conversión de centímetros a metros para cada longitud perteneciente al núcleo. La longitud de la parte superior de la columna derecha es

$l_1 =0.05 \ cm$

$\displaystyle l_1 = 0.05 \ cm \left(\frac{1 \ m}{100 \ cm} \right)$

$l_1 = 0.0005 \ m$

Para la longitud de la parte inferior de la columna derecha es

$l_2 =0.05 \ cm$

$\displaystyle l_2 = 0.05 \ cm \left(\frac{1 \ m}{100 \ cm} \right)$

$l_2 = 0.0005 \ m$

El diámetro efectivo del núcleo del rotor es

$l_r = 5 \ cm$

$\displaystyle l_r = 5 \ cm \left( \frac{1 \ m}{100 \ cm} \right)$

$l_r = 0.05 \ m$

La longitud media del núcleo es

$l_c = 60 \ cm$

$\displaystyle l_c = 60 \ cm \left(\frac{1 \ m}{100 \ cm} \right)$

$l_c = 0.60 \ m$

Y el ancho de cada entre hierro es

$l_g = 0.05 \ cm$

$\displaystyle l_g = 0.05 \ cm \left(\frac{1 \ m}{100 \ cm} \right)$

$l_g = 0.0005 \ m$

Del inciso a), en la figura 1.1.25, una densidad de flujo razonable sería cerca de los 1.2 T. Esto se ve claramente en la figura 1.1.27.

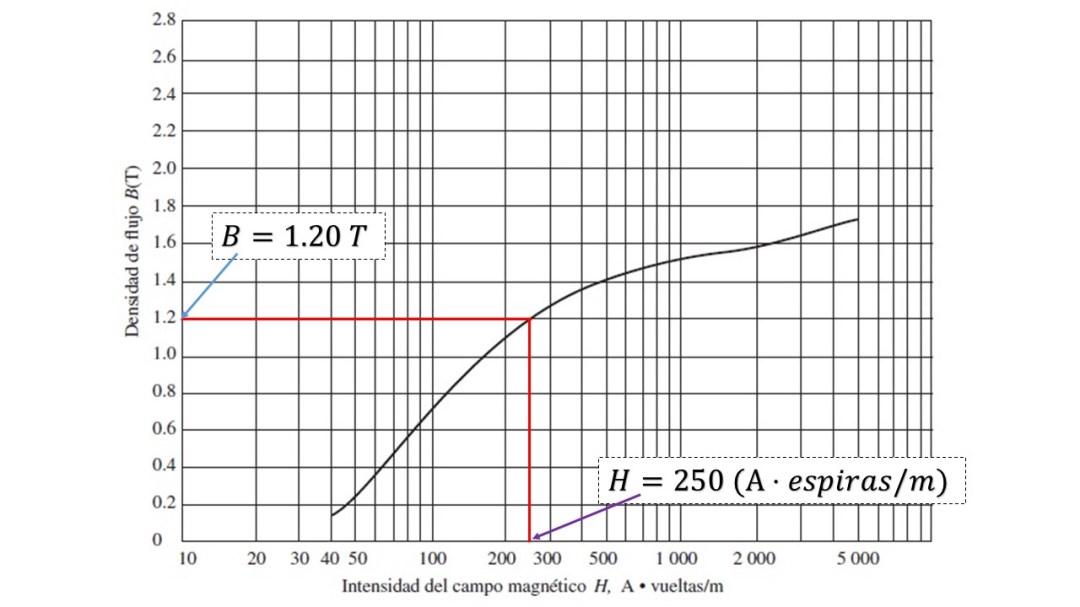
Del inciso b), tomando el valor de la densidad de flujo de 1.2 T, el flujo total será de

$\phi = B \ A$

$\phi = (1.2 \ T)(0.0025 \ m^2)$

$\therefore \phi = 0.003 \ Wb$

Del inciso c) primero se determina la permeabilidad relativa. Partiendo de la curva de magnetización de la figura 1.1.27, y tomando el valor de la densidad de flujo magnético, se observa que la intensidad magnética será de

$H = 250 \ (A \cdot espiras / Wb)$

Calculando la permeabilidad mediante el siguiente despeje

$B = \mu \ H$

$\mu = \frac{B}{H}$

$\displaystyle \mu = \frac{1.2 \ T}{250 \ A \cdot espiras / T}$

$\mu = 0.0048 \ H/m$

Por lo que la permeabilidad relativa es

$\mu = \mu_r \ \mu_0$

$\displaystyle \mu_r = \frac{\mu}{\mu_0}$

$\displaystyle \mu_r = \frac{0.0048 \ H/m}{4 \pi \times 10^{-7} \ H/m}$

$\mu_r \approx 3800$

El cálculo de la permeabilidad relativa también se puede determinar utilizando el valor de la intensidad magnética y la curva de magnetización de la figura 1.1.26.

figura 1.1.28 — Figura 1.1.28 Ubicando el valor de la permeabilidad relativa teniendo el valor de la intensidad magnética.

Ahora, se determinará la reluctancia total. Para ello, el núcleo tiene diferentes dimensiones, provocando que los datos de obtengan por partes. Así que, es necesario obtener el valor de la reluctancia del estator, del entrehierro de la parte superior, del entrehierro de la parte inferior y del rotor. Entonces, la reluctancia del estator es

$\displaystyle \mathcal{R}_{estator} = \frac{l_c}{\mu \ A_{estator}}$

$\displaystyle \mathcal{R}_{estator} = \frac{0.60 \ m}{(0.0048 \ H/m)(0.0025 \ m^2)}$

$\mathcal{R}_{estator} = 50,000 \ (A \cdot espiras / Wb)$

El valor de la reluctancia del entrehierro de la parte superior de la columna derecha es

$\displaystyle \mathcal{R}_1 = \frac{l_1}{\mu \ A_1}$

$\displaystyle \mathcal{R}_1 = \frac{0.0005 \ m}{(4 \pi \times 10^{-7} H/m) (0.0018 \ m^2)}$

$\mathcal{R}_1 = 221,048.02 \ (A \ espiras / Wb)$

El valor de la reluctancia en la parte inferior del entrehierro de la columna derecha es

$\displaystyle \mathcal{R}_2 = \frac{l_2}{\mu \ A_2}$

$\displaystyle \mathcal{R}_2 = \frac{0.0005 \ m}{(4 \pi \times 10^{-7} H/m) (0.0018 \ m^2)}$

$\mathcal{R}_2 = 221,048.02 \ (A \ espiras / Wb)$

Y la reluctancia del rotor es

$\displaystyle \mathcal{R}_{rotor} = \frac{l_{rotor}}{\mu \ A_{rotor}}$

$\displaystyle \mathcal{R}_{rotor} = \frac{0.05 \ m}{(0.0048 \ H/m)(0.0025 \ m^2)}$

$\mathcal{R}_{rotor} = 4,166.67 \ (A \ espiras / Wb)$

En la figura 1.1.28 se tiene un circuito similar al análisis del núcleo del motor. Cómo se puede observar, para determinar la reluctancia total basta con utilizar la suma directa de reluctancia (idéntico a las resistencias en serie).