Problema 8.

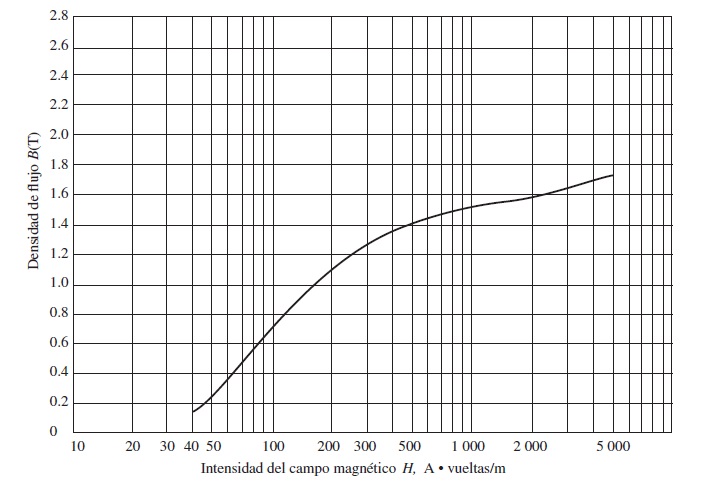
El núcleo de un transformador, cuya trayectoria media efectiva es de 6 pulgadas, tiene una bobina de 200 vueltas enrollada alrededor de una de sus columnas. El área de su sección transversal es de 0.25 pulg^2, y su curva de magnetización se muestra en la figura 1.1.22. Si en la bobina fluye una corriente de 0.3 A, ¿cuál será el flujo total en el núcleo? ¿Cuál es la densidad de flujo?

figura 1.1.22
Figura 1.1.22 Curva de magnetización para el núcleo de un transformador.

Solución.

Primero se convierte la longitud media efectiva de pulgadas a metros.

\displaystyle l = 6 \ pulg \left(\frac{0.0254 \ m}{1 \ pulg} \right)

l = 0.1524 \ m

Después, por medio de la fórmula de la fuerza magnetomotriz y la igualación de despeja la variable H.

\mathcal{F} = N \ i

H \ l = N \ i

\displaystyle H = \frac{N \ i}{l}

\displaystyle H = \frac{(200 \ espiras)(0.3 \ A)}{0.1524 \ m}

H = 393.7 \ A \cdot espiras / m

Tomando el valor de la intensidad magnética y la curva de magnetización, se observa el valor indicado para la densidad de flujo.

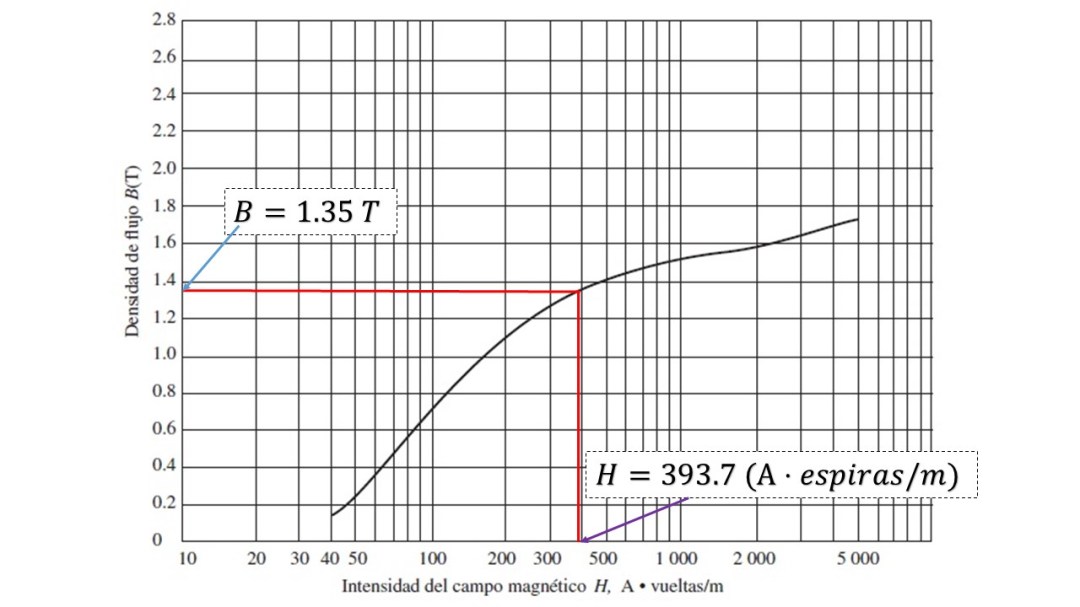
figura 1.1.23
Figura 1.1.23 Ubicación del valor de la densidad de flujo con el apoyo del valor de la intensidad magnética.

Entonces, la densidad de flujo es

\therefore B = 1.35 \ T

Convirtiendo el valor del área expresado en pulgadas cuadradas a metros cuadrados, se tiene que

\displaystyle A = (0.25 \ pulg^2) \left(\frac{0.0254 \ m}{1 \ pulg} \right)^2

A = 0.00016 \ m^2

Asi que, el flujo total es

\phi = B \ A

\phi = (1.35 \ T)(0.00016 \ m^2)

\therefore \phi = 0.000216 \ Wb = 0.216 \ \times 10^{-3} \ Wb = 0.216 \ m Wb

Se concluye que el flujo total que circula en el núcleo es de 0.216 mWb con una densidad de flujo de 1.35 T.

Avatar de Desconocido

Publicado por Cesar Reyes

Dedicado a compartir información temas referentes al cálculo básicos, intermedios y avanzados mediante presentaciones PDF, videos y publicaciones en este sitio web.

Deja un comentario

Este sitio utiliza Akismet para reducir el spam. Conoce cómo se procesan los datos de tus comentarios.