Ecuaciones homogéneas y no homogéneas. Ecuaciones diferenciales

Introducción

Las variables de la ecuación $M(x,y)dx + N(x,y)dy = 0$ se pueden separar si es posible escribir la ecuación de la forma:

$f_1(x)\cdot g_2(y) dx + f_2(x) \cdot g_1(y) dy = 0$ – – – – (1)

El factor integrante $\displaystyle \frac{1}{f_2(x) \cdot g_2(y)}$ hallado simplemente observando la forma de la ecuación , que se transformar de la siguiente manera:

$\displaystyle \frac{f_1(x)}{f_2(x)} dx + \frac{g_1(y)}{g_2(y)} dy = 0$ – – – (2)

en donde se puede obtener por integración la primitiva.

Ecuaciones homogéneas

Una función f(x,y) se llama homogénea de grado «n» si

$f(\lambda x, \lambda y) = {\lambda}^{n} f(x,y)$ – – – – (3)

La ecuación diferencial $M(x,y)dx + N(x,y)dy = 0$ se denomina homogénea si M(x,y) y N(x,y) son homogéneas y del mismo grado.

La transformación $y = vx$ y $dy = v dx + x dv$ reduce cualquier ecuación homogénea a la forma $P(x,v) dx + Q(x,v) dy = 0$ en la que las variables se pueden separar. Después de integrar, se sustituye $v$ por $\displaystyle \frac{y}{x}$ para recobrar las variables originales.

Ecuaciones en las que $M(x,y)$ y $N(x,y)$ son lineales pero no homogéneas

Caso 1. La ecuación $(a_1 x + b_1 y + c_1)dx + (a_2 x + b_2 y + c_2)dy = 0$ , $(a_1 b_2 - a_2 b_1 = 0)$ , se reduce por la transformación:

$a_1 x + b_1 y = t$ , $\displaystyle dy = \frac{dt - a_1 dx}{b_1}$

a la forma

$P(x,t) dx + Q(x,t) dt = 0$ – – – – – (4)

en la que las variables son separables.

Caso 2. La ecuación $(a_1 x + b_1 y + c_1)dx + (a_2 x + b_2 y + c_2)dy = 0$ , $(a_1 b_2 - a_2 b_1 \ne 0)$ , se reduce por la transformación:

$x = x' + h$ , $y = y' + h$

en la que $x=h$ , $y=k$ son las soluciones de las ecuaciones

$a_1 x + b_1 y + c_1 = 0$ y $a_2 x + b_2 y + c_2 = 0$

Problemas resueltos

Problema 1. Resolver $(x^3 + y^3) \ dx - 3xy^2 \ dy = 0$ .

Solución. Se identifica si la ecuación diferencial es homogénea

$[(\lambda x)^3 + (\lambda y)^3] \ dx - 3(\lambda x)(\lambda y)^2 \ dy = 0$

$(\lambda^3 x^3 + \lambda^3 y^3) \ dx - 3 \lambda^3 x y^2 \ dy = 0$

$\lambda^3[(x^3 + y^3) \ dx - 3xy^2 \ dy] = 0$

Esta ecuación diferencial es homogénea de grado 3. Utilizando la transformación $y=vx$ y determinando su diferencial

$\displaystyle \frac{dy}{dx} = \frac{d}{dx}(vx)$

$\displaystyle \frac{dy}{dx} = x \frac{dv}{dx} + v \frac{dx}{dx} = x \frac{dv}{dx} + v$

$dy = x \ dv + v \ dx$

Se sustituye en la ecuación diferencial del problema

$(x^3 + y^3) \ dx - 3xy^2 dy = 0$

$(x^3 + v^3 x^3) \ dx - 3x v^2 x^2 (x \ dv + v \ dx)=0$

$(x^3 + v^3 x^3) \ dx - 3x^4 v^2 \ dv - 3x^3 v^3 \ dx = 0$

$(x^3 + v^3 x^3 - 3x^3 v^3 ) \ dx - 3x^4 v^2 \ dv = 0$

$(x^3 - 2 v^3 x^3) \ dx - 3x^4 v^2 \ dv = 0$

$x^3 (1 - 2 v^3) \ dx + (-3x^4) v^2 \ dv = 0$

Comparando la ecuación diferencial con la forma general

$f_1(x)\cdot g_2(v) dx + f_2(x) \cdot g_1(v) dv = 0$

Se puede determinar el factor integrantes, ya que se puede resolver utilizando el método de separación de variables.

$\displaystyle \frac{1}{f_2 (x) \ g_2 (v)} = \frac{1}{(-3x^4)(1-2v^3)}$

Multiplicando el factor integrante por toda la ecuación diferencial transformada, resulta que

$\displaystyle \frac{1}{(-3x^4)(1-2v^3)}[x^3 (1 - 2 v^3) \ dx + (-3x^4) v^2 \ dv = 0]$

$\displaystyle \frac{1}{(-3x^4)(1-2v^3)}[x^3 (1 - 2 v^3)] \ dx + \frac{1}{(-3x^4)(1-2v^3)}[(-3x^4) v^2] \ dv = 0$

$\displaystyle \frac{1}{-3x} \ dx + \frac{v^2}{(1-2v^3)} \ dv = 0$

$\displaystyle - \frac{1}{3} \cdot \frac{1}{x} \ dx + \frac{v^2}{(1-2v^3)} \ dv = 0$

Integrando en ambos miembros

$\displaystyle - \frac{1}{3} \int{\frac{1}{x} \ dx} + \int{\frac{v^2}{(1-2v^3)} \ dv} = \int{0 \ dx}$

$\displaystyle -\frac{1}{3} \ln{x} - \frac{1}{6} \ln{(1-2v^3)} = C$

$\displaystyle -6 \left[-\frac{1}{3} \ln{x} - \frac{1}{6} \ln{(1-2v^3)} \right] = -6C$

$\displaystyle 2 \ln{x} + \ln{(1-2v^3)} = C$

$\displaystyle \ln{x^2} + \ln{(1-2v^3)} = C$

$\displaystyle \ln{(x^2)(1-2v^3)} = C$

$\displaystyle \ln{(x^2)(1-2v^3)} = \ln{e^C} = \ln{C}$

$\displaystyle x^2(1-2v^3) = C$

Recordando que $y=vx$ , despejándolo $v = y/x$ y sustituyéndolo en la primitiva, se obtiene el resultado final

$\displaystyle x^2 \left[1- 2\left( \frac{y}{x} \right)^3 \right] = C$

$\displaystyle x^2 \left(1- \frac{2y^3}{x^3} \right) = C$

$\displaystyle x^2 \left(\frac{x^3 - 2y^3}{x^3} \right) = C$

$\displaystyle \frac{x^3 - 2y^3}{x} = C$

$\therefore x^3 - 2y^3 = Cx$

Problema 2. Resolver $\displaystyle \left(2x \ Sh \frac{y}{x} + 3y \ Ch \frac{y}{x} \right) dx - 3x \ Ch \frac{y}{x} \ dy = 0$ .

Solución. Primero se identifica si la ecuación diferencial es homogénea.

$\displaystyle \left(2\lambda x \ Sh \frac{\lambda y}{\lambda x} + 3 \lambda y \ Ch \frac{\lambda y}{\lambda x} \right) dx - 3 \lambda x \ Ch \frac{\lambda y}{\lambda x} \ dy = 0$

$\displaystyle \left(2\lambda x \ Sh \frac{y}{x} + 3 \lambda y \ Ch \frac{y}{x} \right) dx - 3 \lambda x \ Ch \frac{y}{x} \ dy = 0$

$\displaystyle \lambda \left(2 x \ Sh \frac{y}{x} + 3 y \ Ch \frac{y}{x} \right) dx - 3 \lambda x \ Ch \frac{y}{x} \ dy = 0$

$\displaystyle \lambda \left[\left(2 x \ Sh \frac{y}{x} + 3 y \ Ch \frac{y}{x} \right) dx - 3 x \ Ch \frac{y}{x} \ dy \right] = 0$

Esta ecuación diferencial es de grado 1. Tomando la transformación $y = vx$ y su diferencial $dy = x \ dv + v \ dx$ , se sustituye en la ecuación diferencial del problema

$\displaystyle \left(2x \ Sh \frac{y}{x} + 3y \ Ch \frac{y}{x} \right) dx - 3x \ Ch \frac{y}{x} \ dy = 0$

$\displaystyle \left(2x \ Sh \frac{vx}{x} + 3vx \ Ch \frac{vx}{x} \right) dx - 3x \ Ch \frac{vx}{x} \ (x \ dv + v \ dx) = 0$

$\displaystyle \left(2x \ Sh \ v + 3vx \ Ch \ v \right) dx - 3x \ Ch \ v \ (x \ dv + v \ dx) = 0$

$\displaystyle \left(2x \ Sh \ v + 3vx \ Ch \ v \right) dx - 3x^2 \ Ch \ v \ dv - 3x v \ Ch \ v \ dx = 0$

$\displaystyle \left(2x \ Sh \ v + 3vx \ Ch \ v - 3xv \ Ch \ v \right) dx - 3x^2 \ Ch \ v \ dv = 0$

$\displaystyle 2x \ Sh \ v \ dx - 3x^2 \ Ch \ v \ dv = 0$

Comparando la ecuación diferencial con la forma general

$f_1(x)\cdot g_2(v) dx + f_2(x) \cdot g_1(v) dv = 0$

Se puede determinar el factor integrantes, ya que se puede resolver utilizando el método de separación de variables.

$\displaystyle \frac{1}{f_2 (x) \ g_2 (v)} = \frac{1}{(-3x^2)(Sh \ v)}$

Multiplicando el factor integrante por toda la ecuación diferencial transformada, resulta que

$\displaystyle \frac{1}{(-3x^2)(Sh \ v)} \left(2x \ Sh \ v \ dx - 3x^2 \ Ch \ v \ dv = 0 \right)$

$\displaystyle \frac{1}{(-3x^2)(Sh \ v)} (2x \ Sh \ v) \ dx - \frac{1}{(-3x^2)(Sh \ v)} (3x^2 \ Ch \ v ) \ dv = 0$

$\displaystyle - \frac{2}{3x} \ dx + \frac{Ch \ v}{Sh \ v} \ dv = 0$

Integrando en ambos miembros

$\displaystyle -\int{\frac{2}{3x} \ dx} + \int{\frac{Ch \ v}{Sh \ v} \ dv} = \int{0 \ dx}$

$\displaystyle -\frac{2}{3} \int{\frac{1}{x} \ dx} + \int{\frac{Ch \ v}{Sh \ v} \ dv} = \int{0 \ dx}$

$\displaystyle -\frac{2}{3} \ln{x} + \ln{Sh \ v} = C$

$\displaystyle \ln{x^{-2/3}} + \ln{Sh \ v} = C$

$\displaystyle \ln{x^{-2/3} Sh \ v} = \ln{e^C} = \ln{C}$

$\displaystyle x^{-2/3} Sh \ v = C$

$\displaystyle \frac{Sh \ v}{x^{2/3}} = C$

$\displaystyle Sh \ v = Cx^{2/3}$

Recordando que $y=vx$ o despejando $v=y/x$ , se tiene el resultado final

$\displaystyle \therefore Sh \frac{y}{x} = C x^{2/3}$

Problema 3. Resolver $\displaystyle (1+2e^{x/y}) dx + 2e^{x/y} \left(1 - \frac{x}{y} \right) dy = 0$ .

Solución. Primero se identifica si la ecuación diferencial es homogenea.

$\displaystyle (1+2e^{\lambda x/ \lambda y}) dx + 2e^{\lambda x/\lambda y} \left(1 - \frac{\lambda x}{\lambda y} \right) dy = 0$

$\displaystyle (1+2e^{x/y}) dx + 2e^{x/y} \left(1 - \frac{x}{y} \right) dy = 0$

Se observa que la ecuación diferencial es homogénea de grado cero.

Tomando la transformación $y = vx$ y su diferencial $dy = v \ dx + x \ dv$ , se sustituye en la ecuación diferencial del problema

$\displaystyle (1+2e^{x/vx}) dx + 2e^{x/vx} \left(1 - \frac{x}{vx} \right) (v \ dx + x \ dv) = 0$

$\displaystyle (1+2e^{1/v}) dx + 2e^{1/v} \left(1 - \frac{1}{v} \right) (v \ dx + x \ dv) = 0$

$\displaystyle (1+2e^{1/v}) dx + 2e^{1/v} \left(v - \frac{v}{v} \right) dx + 2e^{1/v} \left(x - \frac{x}{v} \right) dv = 0$

$\displaystyle (1+2e^{1/v}) dx + 2e^{1/v} \left(v - 1 \right) dx + 2e^{1/v} \left(x - \frac{x}{v} \right) dv = 0$

$\displaystyle (1+2e^{1/v} + 2ve^{1/v} - 2e^{1/v} ) dx + 2e^{1/v} \left(x - \frac{x}{v} \right) dv = 0$

$\displaystyle (1 + 2ve^{1/v}) dx + 2x e^{1/v} \left(1 - \frac{1}{v} \right) dv = 0$

Comparando la ecuación diferencial con la forma general

$f_1(x)\cdot g_2(v) dx + f_2(x) \cdot g_1(v) dv = 0$

Se puede determinar el factor integrantes, ya que se puede resolver utilizando el método de separación de variables.

$\displaystyle \frac{1}{f_2 (x) \ g_2 (v)} = \frac{1}{(2x)(1 + 2ve^{1/v})}$

Multiplicando el factor integrante por toda la ecuación diferencial transformada, resulta que

$\displaystyle \frac{1}{(2x)(1 + 2ve^{1/v})} \left[(1 + 2ve^{1/v}) dx + 2x e^{1/v} \left(1 - \frac{1}{v} \right) dv = 0 \right]$

$\displaystyle \frac{1}{(2x)(1 + 2ve^{1/v})} (1 + 2ve^{1/v}) dx + \frac{1}{(2x)(1 + 2ve^{1/v})} \left[2x e^{1/v} \left(1 - \frac{1}{v} \right) \right] dv = 0$

$\displaystyle \frac{1}{2x} dx + \frac{\left(1 - \frac{1}{v} \right) e^{1/v}}{(1 + 2ve^{1/v})} \ dv = 0$

Integrando en ambos miembros

$\displaystyle \int{\frac{1}{2x} \ dx} + \int{\frac{\left(1 - \frac{1}{v} \right) e^{1/v}}{(1 + 2ve^{1/v})} \ dv} = \int{0 \ dx}$

$\displaystyle \frac{1}{2} \ln{x} + \frac{1}{2} \ln{(1 + 2ve^{1/v})} = C$

$\displaystyle \ln{x} + \ln{(1 + 2ve^{1/v})} = 2C$

$\displaystyle \ln{x} + \ln{(1 + 2ve^{1/v})} = C$

$\displaystyle \ln{x(1 + 2ve^{1/v})} = \ln{C}$

$\displaystyle x(1 + 2ve^{1/v}) = C$

Recordando que $y=vx$ o $v=y/x$

$\displaystyle x(1 + 2\cdot \frac{y}{x}e^{x/y}) = C$

$\displaystyle x \left(\frac{x + 2y e^{x/y}}{x} \right) = C$

$\displaystyle \therefore x + 2y e^{x/y} = C$

Problema 4. Resolver $(x+y) dx + (3x+3y-4)dy=0$ .

Solución. Esta ecuación diferencial es lineal pero no homogénea. Para este caso se utiliza la siguiente transformación.

$x + y =t$

Donde cada función tiene la siguiente expresión: $x+y$ y $3x+3y$ . Ahora, despejando $y$ , la transformación resulta $y = t - x$ ; su diferencia es dy = dt – dx$. Aplicándolo en la ecuación diferencial del problema, resulta lo siguiente

$(x+y)\ dx + (3x + 3y - 4) \ dy = 0$

$t \ dx + (3t - 4) \ (dt - dx) = 0$

$t \ dx + (3t - 4) \ dt - (3t-4) \ dx= 0$

$(t - 3t + 4)dx + (3t-4) dt = 0$

$(-2t + 4) \ dx + (3t - 4)\ dt = 0$

Comparando la ecuación diferencial con la forma general

$f_1(x)\cdot g_2(t) dx + f_2(x) \cdot g_1(t) dt = 0$

Se puede determinar el factor integrantes, ya que se puede resolver utilizando el método de separación de variables.

$\displaystyle \frac{1}{f_2 (x) \ g_2 (t)} = \frac{1}{(1)(-2t + 4)} = \frac{1}{-2t+4}$

Multiplicando el factor integrante por toda la ecuación diferencial transformada, resulta que

$\displaystyle \frac{1}{-2t+4} [(-2t+4) \ dx + (3t-4) \ dt = 0]$

$\displaystyle dx + \frac{3t-4}{-2t + 4} \ dt = 0$

Realizando la división

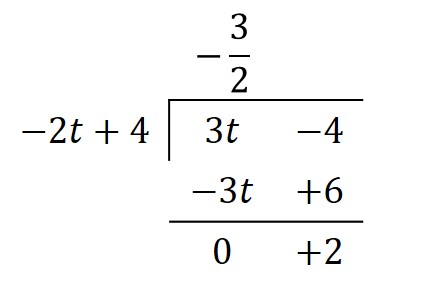
Entonces

$\displaystyle dx + \left(-\frac{3}{2} + \frac{2}{-2t+4} \right) \ dt = 0$

Integrando en ambos miembros

$\displaystyle \int{dx} - \frac{3}{2} \int{dt} + \int{\frac{2}{-2t+4} \ dt} = \int{0 \, dx}$

$\displaystyle x - \frac{3}{2}t - \ln{-2t + 4} = C$

Recordando que $t = x+y$ , se tiene el resultado esperado

$\displaystyle x - \frac{3}{2}(x+y) - \ln{(-2x - 2y + 4)} = C$

$\displaystyle - \frac{1}{2} x - \frac{3}{2} y - \ln{(4 -2x - 2y)} = C$

$\displaystyle \therefore x + 3 y + 2 \ln{(4 -2x - 2y)} = C$

Problema 5. Resolver $(2x - 5y + 3)\ dx - (2x+4y-6) \ dy = 0$

Solución. Esta ecuación diferencial es lineal pero no es homogénea. Para ello, se aplica el siguiente procedimiento: resolviendo los términos de la ecuación como un sistema de ecuaciones lineales con dos incógnitas.

$2x - 5y + 3=0$ , $2x + 4y - 6 = 0$

Resolviendo este sistema, los valores son $x = 1$ y $y=1$ . Para esta transformación, $h=x=1$ y $k=y=1$ . sustituyendo lo siguiente

$x=x' + h$ , $y = y' + k$

$x= x'+1$ , $y = y'+1$

Determinando sus diferenciales

$dx = dx'$ , $dy = dy'$

Sustituyendo en la ecuación diferencial

$(2x - 5y + 3) \ dx - (2x + 4y - 6) \ dy=0$

$[2(x'+1) - 5(y'+1) + 3] \ dx' - [2(x'+1) + 4(y'+1) - 6] \ dy' = 0$

$(2x' - 5y') \ dx' - (2x' + 4y') \ dy' = 0$

Esta ecuación diferencial transformada tiene una oportunidad más de ser verificada si es homogénea o no. Entonces

$(2\lambda x' - 5 \lambda y') \ dx' - (2 \lambda x' + 4 \lambda y') \ dy' = 0$

$\lambda (2x' - 5y') \ dx' - \lambda (2x' + 4y') \ dy' = 0$

Y efectivamente, con esta transformación aplicada en la ecuación diferencial, es homogénea de primer grado (o grado uno).

Tomando $y' = vx'$ y $dy' = v \ dx' + x' \ dv$ , se sustituye en la ecuación diferencial transformada.

$(2x' - 5vx') \ dx' - (2x' + 4vx')(v \ dx' + x' \ dv) = 0$

$(2x' - 5vx') \ dx' - (2x'v + 4v^2 x') \ dx' - (2x'^2 + 4vx'^2) \ dv = 0$

$(2x' - 5vx' - 2x'v - 4v^2 x') \ dx' - (2x'^2 + 4v x'^2) \ dv = 0$

$(2x' - 7x'v - 4x' v^2) \ dx' - (2x'^2 + 4v x'^{2}) \ dv= 0$

$x' (2 - 7v - 4v^2) \ dx' - x'^2 (2 + 4v) \ dv = 0$

Comparando la ecuación diferencial con la forma general

$f_1(x') \cdot g_2(v) dx' + f_2(x') \cdot g_1(v) dv = 0$

Se puede determinar el factor integrantes, ya que se puede resolver utilizando el método de separación de variables.

$\displaystyle \frac{1}{f_2 (x') \ g_2 (v)} = \frac{1}{(-x'^2)(2-7v-4v^2)}$

Multiplicando el factor integrante por toda la ecuación diferencial transformada, resulta que

$\displaystyle \frac{1}{(-x'^2)(2-7v-4v^2)} [x' (2 - 7v - 4v^2) \ dx' - x'^2 (2 + 4v) \ dv = 0]$

$\displaystyle \frac{1}{(-x'^2)(2-7v-4v^2)} [x' (2 - 7v - 4v^2)] \ dx' - \frac{1}{(-x'^2)(2-7v-4v^2)} [x'^2 (2 + 4v)] \ dv = 0$

$\displaystyle -\frac{1}{x'} \ dx' + \frac{(2+4v)}{(2-7v-4v^2)} \ dv = 0$

$\displaystyle -\frac{1}{x'} \ dx' - \frac{(2+4v)}{(-2+7v+4v^2)} \ dv = 0$

$\displaystyle \frac{1}{x'} \ dx' + \frac{(2+4v)}{(-2+7v+4v^2)} \ dv = 0$

Del segundo termino, se puede resolver por fracciones parcial, por lo que su resultado es

$\displaystyle \frac{(2+4v)}{(-2+7v+4v^2)} = \frac{(2+4v)}{\frac{1}{4}(v+2)(4v-1)} = \frac{2/3}{(v+2)} + \frac{4/3}{(4v-1)}$

Regresando

$\displaystyle \frac{1}{x'} \ dx' + \frac{(2+4v)}{(-2+7v+4v^2)} \ dv = 0$

$\displaystyle \frac{1}{x'} \ dx' + \frac{2/3}{(v+2)} \ dv + \frac{4/3}{(4v-1)} \ dv = 0$

$\displaystyle \frac{3}{x'} \ dx' + \frac{2}{(v+2)} \ dv + \frac{4}{(4v-1)} \ dv = 0$

Integrando cada término y en ambos miembros

$\displaystyle \int{\frac{3}{x'} \ dx'} + \int{\frac{2}{(v+2)} \ dv} + \int{\frac{4}{(4v-1)} \ dv} = \int{0 \ dx'}$

$\displaystyle 3 \ln{x'} + 2 \ln{(v+2)} + \ln{(4v-1)} = C$

$\displaystyle \ln{x'^3} + \ln{(v+2)^2} + \ln{(4v-1)} = \ln{e^C}$

$\displaystyle \ln{(x'^3) (v+2)^2 (4v-1)} = \ln{C}$

$x'^3 (v+2)^2 (4v-1) = C$

Recordando que $v = y'/x'$ , el resultado se transforma en

$\displaystyle x'^3 \left(\frac{y'}{x'} + 2 \right)^2 \left(\frac{4y'}{x'} - 1\right) = C$

$\displaystyle x'^3 \left(\frac{y' + 2x'}{x'} \right)^2 \left( \frac{4y' - x'}{x'} \right) = C$

$\displaystyle (2x' + y')^2 (4y' - x') = C$

recordando también que $x=x'+1$ y $y = y'+1$ , se despejan ambas ecuaciones las variables $x'$ y $y'$ (es decir, $x' = x-1$ y $y' = y-1$ ), y se sustituyen en la ultima expresión obtenida.