Soluciones singulares y lugares geométricos extraños. Ecuaciones diferenciales.

Soluciones singulares.

Una solución singular de una ecuación diferencial satisface la ecuación diferencial, pero no es una solución particular de la ecuación.

En cada punto de su lugar geométrico (envolvente) el número de direcciones distintas que da la ecuación diferencial y el número de curvas distintas que da la primitiva correspondiente son menores que en los puntos que no pertenecen al lugar geométrico.

Las soluciones singulares de una ecuación diferencial se encuentran expresando las condiciones:

a) que la ecuación diferencial (ecuación $p$ ) tenga raíces múltiples, y
b) que la primitiva (ecuación $C$ ) tenga raíces múltiples.

En general, una ecuación de primer orden no tiene soluciones singulares; si es de primer grado no puede tener soluciones singulares. Aún más, una ecuación $f(x,y,p) = 0$ no puede tener solucione singulares si $f(x,y,p)$ puede resolverse según factores que sean lineales en $p$ y racionales en $x$ y $y$ .

La expresión más sencillo, llamada el discriminante, que contienelos coeficiente de una ecuación $F(x) = 0$ cuya anulación es la condición para que la ecuación tenga raíces múltiples, se obtiene eliminando $X$ entre $F(X) = 0$ y $F'(X) = 0$ . El discriminante de

$\displaystyle aX^2 + bX + c = 0$ es $b^2 -4ac$

$aX^3 + bX^2 + cX + d = 0$ es $b^2 c^2 +18 abcd - 4a c^3 - 4b^3 d - 27a^2 d^2$

Si $E(x,y) = 0$ es una solución singular de la ecuación diferencial $f(x,y,p) = 0$ cuya primitiva es $g(x,y,C) = 0$ , entonces $E(x,y)$ es un factor de ambos discriminantes. Sin embargo, cada discriminante puede tener otros factores que originan otros lugares geométricos asociados con la primitiva. Como las ecuaciones de estos lugares geométricos generalmente no satisfacen la ecuación diferencial se denominan extraños.

Lugares geométricos extraños.

Para este caso se toma en cuenta la ecuación diferencial $f(x,y,p) = 0$ y la primitiva $g(x,y,C) = 0$ .

Lugar de choque. Sea $P$ un punto en el que dos o más de las $n$ curvas distintas de la familia $g(x,y,C) = 0$ que pasan por él tienen una tangente en común. Entonces, el número de direcciones distintas en $P$ es inferior a $n$ por lo que se tiene que anular aquí el discriminante $p$ . El lugar geométrico, en caso de que exista, de todos los puntos de este tipo se denomina lugar de choque. Si $T(x,y)=0$ es la ecuación del lugar de choque, entonces $T(x,y)$ es un factor del discriminante $p$ . En general $T(x,y)$ no es un factor discriminantes $C$ y $T(x,y) =0$ no satisface la ecuación diferencial.

Figura 1.11.1 Representando una familia de curvas para mostrar un lugar de puntos de choque.

Lugar de puntos dobles. Esto se debe a que una de las curvas de la familia pasa por un punto $P$ tal que es doble con tangentes distintas. Como ya se tienen así en cuenta dos de los $n$ valores de $p$ , no puede haber más de $n-1$ curvas distintas por el punto $P$ ; luego el discriminante $C$ se anula en $P$ . El lugar geométrico, en caso de que haya uno, de todos los puntos de este tipo se denomina un lugar crunodal o lugar de puntos dobles. Si $N(x,y) = 0$ representa la ecuación del lugar de puntos dobles, $N(x,y)$ es un factor discriminante $C$ . En general, $N(x,y)$ no es un factor discriminante $p$ y $N(x,y) = 0$ no puede satisfacer la ecuación diferencial.

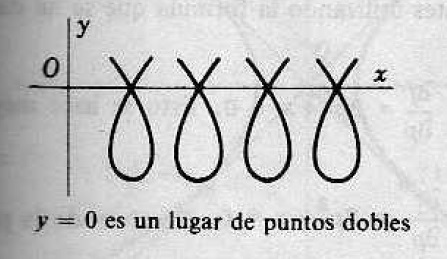
Figura 1.11.2 Representando una familia de curvas para mostrar un lugar de puntos dobles.

Lugares de puntos de retroceso. Suponiendo que una de las curvas de la familia pasa por $P$ y que para ella éste es un punto de retroceso (punto doble con tangentes coincidente), una de las raíces de $p$ es doble, el discriminante $p$ se anula en $P$ . Sin embargo, como en el caso de un punto doble, no puede haber más de $n-1$ curvas por $P$ y el discriminante $C$ se anula en $P$ . El lugar geométrico, si lo hay, de tales puntos es un lugar cuspidal o lugar de puntos de retroceso. Si $C(x,y) = 0$ representa la ecuación del lugar de puntos de retroceso, $C(x,y)$ es un factor tanto del discriminante $p$ como del discriminante $C$ . En general, $C(x,y) = 0$ no satisfac la ecuación diferencial.

Figura 1.11.3 Representando una familia de curvas para mostrar un lugar de puntos de retroceso.

Si las curvas de la familia $g(x,y,C) =0$ son líneas rectas, no hay lugares geométricos extraños.
Si las curvas de la familia son cónicas, no puede haber ni lugares de puntos de retroceso ni de puntos dobles.

El discriminante 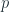$p$ .

El discriminante de la ecuación diferencial $f(x,y,p) = 0$ , el discriminante $p$ , igualado a cero incluye como una factor:

La ecuación de la envolvente (solución singular) una vez; la solución singular satisface la ecuación diferencial.
La ecuación del lugar geométrico de los puntos de retroceso, una vez; la ecuación del lugar geométrico de los puntos de retroceso no satisface la ecuación diferencial a menos que sea también una solución singular o solución particular.
La ecuación del lugar de choque, dos veces; la ecuación del lugar de choque no satisface la ecuación diferencial a menos que sea también una solución singular o solución particular.

El discriminante 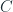$C$ .

El discriminante de la primitiva $g(x,y,C) = 0$ , el discriminante $C$ , igualado a cero incluye como un factor:

La ecuación de la envolvente o solución singular una vez.
La ecuación del lugar geométrico de los puntos de retroceso, tres veces.
La ecuación del lugar geométrico de los puntos dobles, dos veces; la ecuación del lugar geométricode los puntos dobles no satisface la ecuación diferencial a menos que sea también una solución singular o solución particular.

Si un lugar geométrico pertenece a dos categorías, la multiplicidad de su ecuación en una relación discriminante es la suma de la multiplicidades en cada categoría; asi, un lugar geométrico de puntos de retroceso que también es una envolvente está incluido dos veces en la relación discriminante $p$ y cuatro veces en la relación discriminante $C$ .

Sin embargo, la identificación de los lugares geométricos extraños no es una mera contabilidad e multiplicidades de factores.

Soluciones singulares y lugares geométricos extraños. Ecuaciones diferenciales.