16 mayo, 201920 mayo, 2019 Cesar Reyes blog, máquinas eléctricas

Transformadores. Problema 15. Máquinas eléctricas.

Problema. Pruebe la siguiente afirmación: si un transformador con una impedancia en serie $Z_{eq}$ se conecta como autotransformador, su impedancia en serie $Z_{eq}'$ por unidad como autotransformador será de

$\displaystyle Z_{eq}' = \frac{N_{SE}}{N_{SE}+N_C} Z_{eq}$

Nótese que esta expresión es el inverso de la ventaja de potencia del autotransformador.

Solución. La impedancia de este transformador puede encontrarse por cortocircuito del devanado secundario y determinando la razón de voltaje a la corriente de su devanado primario.

Figura 2.15.1

Por este transformador conectado como un transformador ordinario, la impedancia referida al primario ( $N_C$ ) es

$\displaystyle Z_{eq} = Z_1 + a^2 Z_2$

$\displaystyle Z_{eq} = Z_1 + \left(\frac{N_C}{N_{SE}} \right)^2 Z_2$

Así que, el circuito equivalente correspondiente se muestra en la figura 2.15.2.

Figura 2.15.2

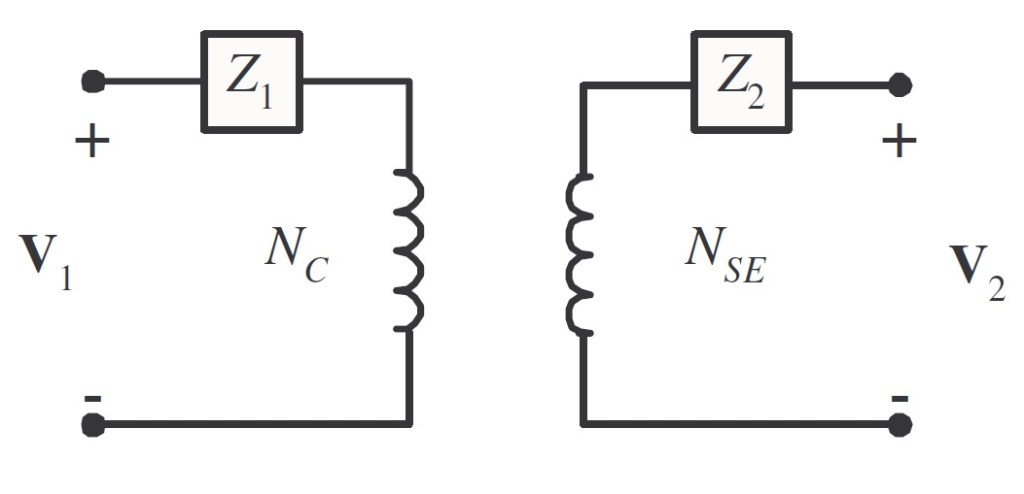
Cuando este transformador está conectado como un autotransformador, el circuito es como se muestra a continuación.

Figura 2.15.3

Si la salida de lo devanados del autotransformador están cortocircuitados, el voltaje $\boldsymbol{V_H}$ será cero y el voltaje $\boldsymbol{V_L}$ será

$\boldsymbol{V_L} = Z_{eq} \boldsymbol{I_C}$

Donde $Z_{eq}$ es la impedancia del transformador ordinario.

Sin embargo,

$\displaystyle \boldsymbol{I_L} = \boldsymbol{I_C} + \boldsymbol{I_{SE}}$

$\displaystyle \boldsymbol{I_L} = \boldsymbol{I_C} + \frac{N_C}{N_{SE}} \boldsymbol{I_C}$

$\displaystyle \boldsymbol{I_L} = \frac{N_{SE} + N_C}{N_{SE}} \boldsymbol{I_C}$

$\displaystyle \boldsymbol{I_C} = \frac{N_{SE}}{N_C} \boldsymbol{I_L}$

Después, el voltaje de entrada puede expresarse en términos de la corriente de entrada.

$\displaystyle \boldsymbol{V_L} = Z_{eq} \boldsymbol{I_C}$

$\displaystyle \boldsymbol{V_L} = Z_{eq} \cdot \frac{N_{SE}}{N_{SE} + N_C} \boldsymbol{I_L}$

Y la impedancia de entrada del autotransformador está definido como

$\displaystyle Z_{eq}' = \frac{\boldsymbol{V_L}}{\boldsymbol{I_L}}$

Entonces, realizando sustituciones, la expresión esperada es

$\displaystyle Z_{eq}' = \frac{\boldsymbol{V_L}}{\boldsymbol{I_L}}$

$\displaystyle Z_{eq}' = \frac{Z_{eq} \cdot \frac{N_{SE}}{N_{SE} + N_C} \boldsymbol{I_L}}{\boldsymbol{I_L}}$

$\displaystyle Z_{eq}' = Z_{eq} \cdot \frac{N_{SE}}{N_{SE} + N_C}$

Finalmente

$\displaystyle \therefore Z_{eq}' = \left(\frac{N_{SE}}{N_{SE} + N_C} \right) Z_{eq}$

Publicado por Cesar Reyes

Dedicado a compartir información temas referentes al cálculo básicos, intermedios y avanzados mediante presentaciones PDF, videos y publicaciones en este sitio web. Ver todas las entradas de Cesar Reyes

Deja un comentario Cancelar la respuesta

Este sitio utiliza Akismet para reducir el spam. Conoce cómo se procesan los datos de tus comentarios.