Introducción a la electrónica de potencia. Problema 1. Máquinas eléctricas.

Problema. Calcule el factor de rizado de circuito rectificador trifásico de media onda, en forma analítica y utilizando MATLAB.

Solución.

Forma analítica. Un rectificador trifásico de media onda y su voltaje de salida son mostrados en la siguiente figura.

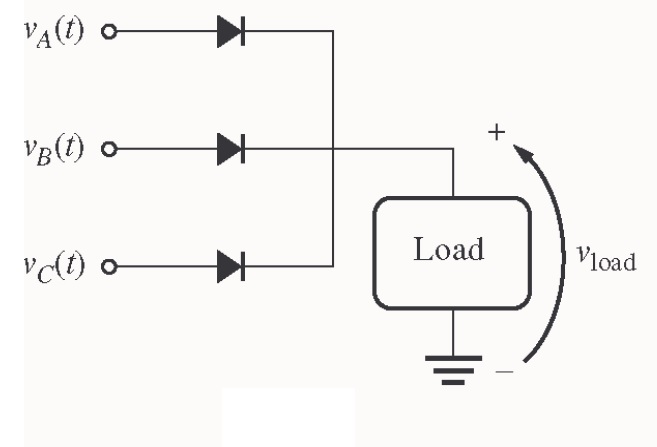
*Figura 3.1.1 Circuito rectificador trifásico de media onda.*

Analizando la forma de onda de la figura 3.1.2, se tiene lo siguiente

$\displaystyle v_A (t) = V_M \sin{\omega t}$

$\displaystyle v_B (t) = V_M \sin{(\omega t - \frac{2\pi}{3})}$

$\displaystyle v_C (t) = V_M \sin{(\omega t + \frac{2\pi}{3})}$

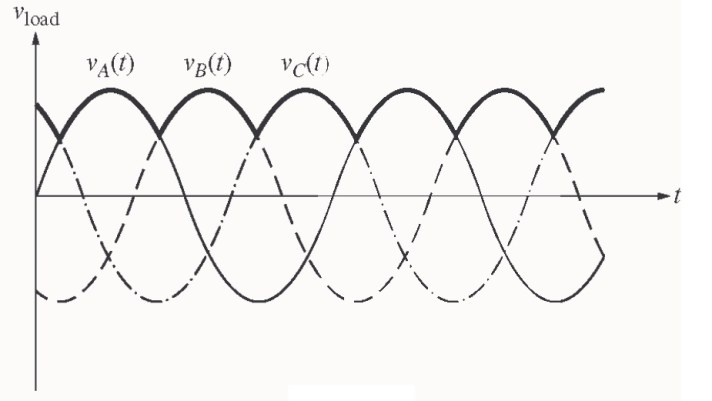
Figura 3.1.2 Forma de onda del rectificador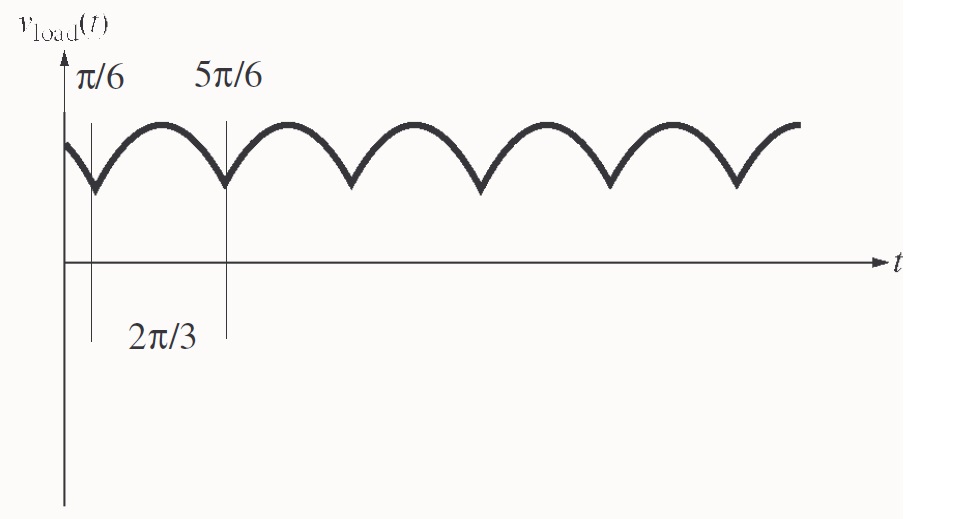
Figura 3.1.3 Análisis de período de la forma de onda del rectificador.

Si se determinan los valores promedio y rms desde el intervalo $\pi/6$ hasta $5 \pi/6$ (un período), estos valores serán los mismos tanto en el valor promedio como el valor rms de toda la forma de onda y estos pueden ser calculados por el factor de rizado. El voltaje promedio es

$\displaystyle V_{CD} = \frac{1}{T} \int{v(t) \ dt}$

$\displaystyle V_{CD} = \frac{1}{T} \int_{\pi/6}^{5\pi/6}{V_M \sin{\omega t} \ d(\omega t)}$

$\displaystyle V_{CD} = \frac{3}{2\pi} V_M \int_{\pi/6}^{5\pi/6}{\sin{\omega t} \ d(\omega t)}$

$\displaystyle V_{CD} = \frac{3}{2\pi} V_M \left[-\cos{\omega t} \right]_{\pi/6}^{5\pi/6} = \frac{3}{2\pi} V_M \left(-\cos{\frac{5\pi}{6}} + \cos{\frac{\pi}{6}}\right)$

$\displaystyle V_{CD} = \frac{3}{2\pi} V_M \left(\frac{\sqrt{3}}{2} + \frac{\sqrt{3}}{2} \right) = \frac{3}{2\pi} V_M \cdot \sqrt{3}$

$\displaystyle \therefore V_{CD} = \frac{3 \sqrt{3}}{2 \pi} V_M = 0.8270 V_M$

El voltaje rms es

$\displaystyle V_{rms} = \sqrt{\frac{1}{T} \int{v^2(t) \ dt}}$

$\displaystyle V_{rms} = \sqrt{\frac{1}{T} \int_{\pi/6}^{5\pi/6}{(V_M \sin{\omega t})^2 \ dt}}$

$\displaystyle V_{rms} = \sqrt{\frac{1}{\frac{2\pi}{3}} \int_{\pi/6}^{5\pi/6}{V_M^2 \sin^2{\omega t} \ dt}}$

$\displaystyle V_{rms} = \sqrt{\frac{3}{2\pi} \cdot V_M^2 \cdot \frac{1}{2} \int_{\pi/6}^{5\pi /6}{(1 - \cos{2\omega t}) \ dt}}$

$\displaystyle V_{rms} = \sqrt{\frac{3}{4\pi} V_M^2 \left[\omega t - \frac{1}{2} \sin{2\omega t} \right]_{\pi / 6}^{5\pi /6}}$

$\displaystyle V_{rms} = \sqrt{\frac{3}{4\pi} V_M^2 \left(\frac{4\pi}{6} - \frac{1}{2} \sin{\frac{5\pi}{3} - \frac{1}{2} \sin{\frac{\pi}{3}}} \right)}$

$\displaystyle V_{rms} = \sqrt{\frac{3}{4\pi} V_M^2 \left(\frac{2\pi}{3} + \frac{1}{2} \cdot \frac{\sqrt{3}}{2} + \frac{1}{2} \cdot \frac{\sqrt{3}}{2} \right)}$

$\displaystyle V_{rms} = \sqrt{\frac{3}{4\pi} V_M^2 \left(\frac{2\pi}{3} + \frac{\sqrt{3}}{4} + \frac{\sqrt{3}}{4} \right)}$

$\displaystyle V_{rms} = \sqrt{\frac{3}{4\pi} V_M^2 \left(\frac{2\pi}{3} + \frac{\sqrt{3}}{2} \right)} = 0.8407 V_M$

Finalmente, el factor de rizado es

$\displaystyle r = \sqrt{\left(\frac{V_{rms}}{V_{CD}} \right)^2- 1} \times 100$ %

$\displaystyle r = \sqrt{\left(\frac{0.8407 V_M}{0.8270 V_M} \right)^2- 1} \times 100$ %

$\displaystyle r = \sqrt{\left(\frac{0.8407 V_M}{0.8270 V_M} \right)^2 - 1} \times 100$ %

$\displaystyle r = (0.183) \times 100$ %

$\displaystyle r = 18.3$ %

Utilizando MATLAB

Primero se escribe el siguiente código y guardarlo en formato .m

 function volts = halfwave3(wt)
 %Función para simular la salida de un rectificador trifásico de media onda.
 %wt = fase en radianes (=omega * time).

 %Convertir la entrada al rango 0<= wt <=2pi while wt >= 2pi
     wt = wt - 2*pi;
 end
 while wt < 0
     wt = wt + 2*pi;
 end

 %Simula la salida del rectificador
 a = sin(wt);
 b = sin(wt - 2pi/3);
 c = sin(wt + 2pi/3);
 volts = max([a b c]);

Al momento de guardarlo, el archivo debe llamarse «halfwave3.m». Después, se elabora otro archivo con el mismo formato y se escribe el siguiente código

 function r = ripple(waveform)

 %Funcion para calcular el rizado de la forma de onda de la entrada.
 
%Calcular el valor promedio de la forma onda
 nvals = size(waveform,2);
 temp = 0;
 for ii = 1:nvals
     temp = temp + waveform(ii);
 end
 promedio = temp/nvals;
 
%Calculo de los valores rms de la forma de onda.
 temp = 0;
 for ii = 1:nvals
     temp = temp + waveform(ii)^2;
 end
 rms = sqrt(temp/nvals);
 
%Cálculo del factor de rizado
 r = sqrt((rms/promedio)^2-1) * 100;

Al momento de guardarlo, el archivo debe llamarse «ripple.m». Por último, se escribe el tercer código de la siguiente manera

 %Archivo .m para calcular el rizado de la salida de un rectificador
 %trifásico de media onda.

 % Primero, se general la salida del rectificador trifásico de media onda.
 waveform = zeros(1,128);
 for ii = 1:128
     waveform(ii) = halfwave3(ii*pi/64);
 end

 %Ahora, se calcula el factor de rizado
 r = ripple(waveform);

 %Muestra el resultado
 string = ['El rizado es de ' num2str(r) '%.'];
 disp(string);

Al momento de guardarlo, el archivo puede llamarse al nombre que usted desee. Finalmente, ejecutando este último archivo, en la ventana «Command Window» imprime lo siguiente

Figura 3.1.4 Resultado del programa visualizado en la ventana Command Window. — Figura 3.1.4 Resultado del programa visualizado en la ventana «Command Window».

Con esto, se termina la solución del problema.

Introducción a la electrónica de potencia. Problema 1. Máquinas eléctricas.

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta

Introducción a la electrónica de potencia. Problema 1. Máquinas eléctricas.

Comparte esto:

Relacionado

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta