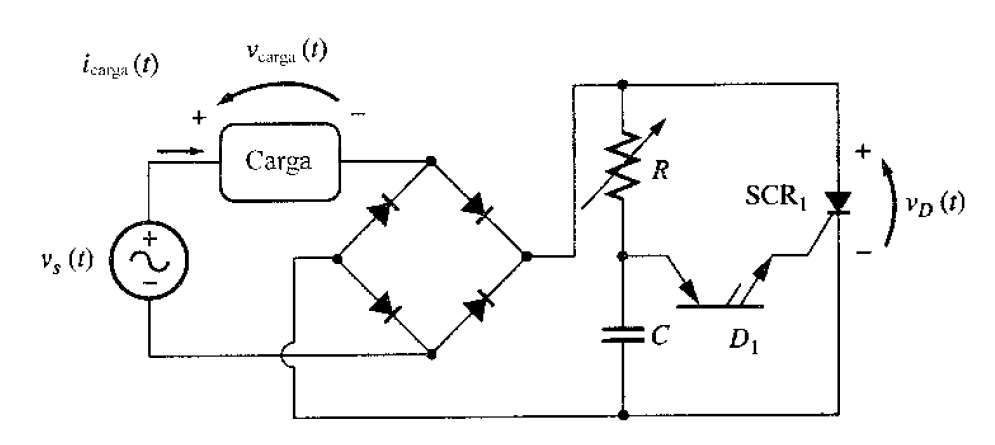
Introducción a la electrónica de potencia. Problema 13. Máquinas eléctricas.

Problema. La figura muestra un controlador sencillo de ángulo de fase, de voltaje ac y de onda completa. Los valores de las componentes del circuito son

$R = 20$ a $300 \ (k\Omega)$ , normalmente colocado en $100 \ (k \Omega)$
$C = 0.1 \ (\mu F)$
$V_{BO} = 40 \ (V)$ (para el diodo PNPN $D_1$ )
$V_{BO} = 250 \ (V)$ (para $SCR_1$ )
$v_s (t) = V_M \sin{\omega t} \ (V)$ donde $V_M = 169.7 \ (V)$ y $\omega =377 \ (m/s)$

a) ¿A qué ángulo de fase se encenderán el diodo PNPN y el SCR?

b) ¿Cuál es el voltaje rms suministrado a la carga en estas circunstancias?

Figura 3.13.1 Circuito controlador sencillo de ángulo de fase de voltaje ac y de onda completa.

Solución. En el comienzo de cada semiciclo, los voltajes a través del diodo PNPN y el SCR ambos serán más pequenos respecto al voltaje de ruptura, por lo que la corriente no fluirá hasta la carga (excepto para muy pequeña corriente de carga del capacitor $C$ ) y $v_{carga} (t)$ será 0 volts. Sin embargo,el capacitor $C$ carga a través de la resistencia $R$ y cuando el voltaje $v_C (t)$ reúna el voltaje de ruptura de $D_1$ , el diodo PNPN empezará a conducir. Esta corriente fluye a través de la compuerta del $SCR_1$ , se enciende el SCR. Cuando se activa, el voltaje a través del SCR disminuirá a cero y el voltaje de la fuente completo $v_S (t)$ estará aplicado a la carga, produciendo un flujo de corriente a la carga. El SCR continua conduciendo hasta que la corriente a través de él cae por debajo de $I_H$ , lo que sucede al final de cada semiciclo.

Se observa que después de $D_1$ se active, el capacitor $C$ se descarga a través de él y la compuerta del SCR. Al final de cada semiciclo, el voltaje en el capacitor nuevamente es esencialmente cero y todo el proceso está listo para volver a comenzar en el siguiente semiciclo.

Para determinar cuando el diodo PNPN y el SCR se activan en este circuito, se debe determinar cuando $v_C (t)$ excede $V_{BO}$ de $D_1$ .

Solución a). Para determinar cuando el SCR se enciende, se debe calcular el voltaje $v_C (t)$ y luego resolver el tiempo en que $v_C (t)$ excede $V_{BO}$ para $D_1$ . Al comienzo de cada semiciclo, $D_1$ y $SCR_1$ está apagados y el voltaje a través de la carga es esencialmente 0, de modo que toda la fuente de voltaje $v_S (t)$ es aplicado al circuito RC en serie. Para determinar el voltaje $v_C (t)$ del capacitor, se utiliza la ley de corriente de Kirchhoff en el nodo sobre el capacitor y resolver la ecuación resultante de $v_C (t)$ .

$\displaystyle \sum{i} = 0$

$\displaystyle i_1 + i_2 = 0$

$\displaystyle \frac{v_C - v_1}{R} + C \frac{d v_C}{dt} = 0$

$\displaystyle \frac{v_C}{R} - \frac{v_1}{R} + C \frac{d v_C}{dt} = 0$

$\displaystyle C \frac{d v_C}{dt} + \frac{1}{R} v_C = \frac{v_1}{R}$

$\displaystyle \frac{d v_C}{dt} + \frac{1}{RC} v_C = \frac{v_1}{RC}$

$\displaystyle \frac{d v_C}{dt} + \frac{1}{RC} v_C = \frac{V_M}{RC}\sin{\omega t}$

Resolviendo por el factor integrante

$\displaystyle v_C \cdot e^{\int{\frac{1}{RC} \ dt}} = \int{\frac{V_M}{RC} \sin{\omega t} \cdot e^{\int{\frac{1}{RC} \ dt}} \ dt}$

$\displaystyle v_C \cdot e^{\frac{1}{RC} t} = \frac{V_M}{RC} \int{e^{\frac{1}{RC} t} \sin{\omega t} \ dt}$

$\displaystyle v_C \cdot e^{\frac{1}{RC} t} = \frac{V_M}{RC} \cdot \left(\frac{1}{\frac{1}{R^2 C^2} + \omega^2} \right) e^{\frac{1}{RC} t} \left(\frac{1}{RC} \sin{\omega t} - \omega \cos{\omega t} \right) + A$

$\displaystyle v_C \cdot e^{\frac{1}{RC} t} = \frac{V_M}{RC} \cdot \left(\frac{R^2 C^2}{1 +R^2 C^2 \omega^2} \right) e^{\frac{1}{RC} t} \left(\frac{1}{RC} \sin{\omega t} - \omega \cos{\omega t} \right) + A$

$\displaystyle v_C \cdot e^{\frac{1}{RC} t} = \frac{V_M}{RC} \cdot \left(\frac{1}{1 +R^2 C^2 \omega^2} \right) e^{\frac{1}{RC} t} \left(RC \sin{\omega t} - \omega R^2 C^2 \cos{\omega t} \right) + A$

$\displaystyle v_C = V_M \cdot \left(\frac{1}{1 +R^2 C^2 \omega^2} \right) \left(\sin{\omega t} - \omega RC \cos{\omega t} \right) + \frac{A}{e^{\frac{1}{RC} t}}$

$\displaystyle v_C (t)= \left(\frac{V_M}{1 +R^2 C^2 \omega^2} \right) \sin{\omega t} - \left( \frac{V_M RC \omega}{1+R^2 C^2 \omega^2} \right) \cos{\omega t} + Ae^{-\frac{1}{RC} t}$

donde $A$ representa la constante de integración; no se tomó en cuenta la variable $C$ para no confundir con el valor de la capacitancia.

Tomando la condición inicial $v_C (0) = 0$ (que significa que el voltaje en el capacitor es cero en el comienzo del semiciclo), el valor de $A$ es

$\displaystyle v_C (0)= \left(\frac{V_M}{1 +R^2 C^2 \omega^2} \right) \sin{\omega (0)} - \left( \frac{V_M RC \omega}{1+R^2 C^2 \omega^2} \right) \cos{\omega (0)} + Ae^{-\frac{1}{RC} (0)}$

$\displaystyle 0 = - \left( \frac{V_M RC \omega}{1+R^2 C^2 \omega^2} \right) + A$

$\displaystyle A = \left( \frac{V_M RC \omega}{1+R^2 C^2 \omega^2} \right)$

Al sustituir en la ecuación $v_C (t)$ , resulta que

$\displaystyle v_C (t)= \left(\frac{V_M}{1 +R^2 C^2 \omega^2} \right) \sin{\omega t} - \left( \frac{V_M RC \omega}{1+R^2 C^2 \omega^2} \right) \cos{\omega t} + \left(\frac{V_M RC \omega}{1+R^2 C^2 \omega^2} \right)e^{-\frac{1}{RC} t}$

Si $R = 100 k\Omega$ , $C = 0.1\mu F$ , $\omega = 377$ y $V_M = 169.7$ , el resultado de $v_C (t)$ es

$\displaystyle v_C (t)= \left[\frac{169.7}{1 +(100 \times 10^3)^2 (0.1\times 10^{-6})^2 (377)^2} \right] \sin{377 t} - \left[ \frac{(169.7)(100 \times 10^{3})(0.1 \times 10^{-6})(377)}{1+(100 \times 10^3)^2 (0.1\times 10^{-6})^2 (377)^2} \right] \cos{377 t} + \left(\frac{169.7 (100 \times 10^3)(0.1 \times 10^{-6})(377)}{1+(100\times 10^3)^2 (0.1\times 10^{-6})^2 (377)^2} \right)e^{-\frac{1}{(100 \times 10^3)(0.1 \times 10^{-6})} t}$

$\displaystyle v_C (t)= 11.155 \sin{377 t} - 42.054 \cos{377 t} + 42.054 e^{-100 t} \ (V)$

Graficando esta expresión mediante MATLAB R2018a, se escribe el siguiente código

 t=0:1/100000:10;
 v = 11.142sin(377t) - 42.005cos(377t) + 42.005exp(-100t);
 figure(1);
 plot(t,v);
 title('\bfVoltaje del capacitor');
 xlabel('\bfTiempo (ms)');
 ylabel('\bfv_C (V)');
 axis([0 0.008 0 70]);
 grid on;

Al momento de guardarlo, el archivo puede llamarse cualquier nombre en formato $atex .m$. Al ejecutarlo, se tiene el resultado

Al localizar el voltaje de 40 (V) en la gráfica (figura 3.13.2), se tiene un tiempo de 0.00426 (s) (4.26 ms). Con la frecuencia de 60 Hz, la forma de onda tiene 360° en 1/60 (s). Así que, el ángulo de disparo $\alpha$ es

$\displaystyle \alpha = (0.00426 \frac{360}{\frac{1}{60}}$

$\displaystyle \therefore \alpha = 92.02$ °

Convirtiendo a radianes

$\displaystyle \alpha = 92.02 (\frac{\pi}{180})$

$\displaystyle \therefore \alpha = 1.606$ (rad)

El voltaje rms aplicado a la carga es

$\displaystyle V_{rms} = \sqrt{\frac{1}{T} \int{v(t)^2 \ dt}}$

$\displaystyle V_{rms} = \sqrt{\frac{1}{\frac{\pi}{\omega}} \int_{\alpha}^{\pi/\omega}{(V_M \sin{\omega t})^2 \ dt}}$

$\displaystyle V_{rms} = \sqrt{\frac{\omega}{\pi} \int_{\alpha}^{\pi/\omega}{V_M^2 \sin^2{\omega t} \ dt}}$

$\displaystyle V_{rms} = \sqrt{\frac{\omega}{\pi} V_M^2 \int_{\alpha}^{\pi/\omega}{(\frac{1}{2} - \frac{1}{2} \cos{2\omega t} \ dt}}$

$\displaystyle V_{rms} = \sqrt{\frac{\omega}{\pi} V_M^2 \left[\frac{1}{2} \omega t + \frac{1}{4} \sin{2\omega t} \right]_{\alpha}^{\pi/\omega}}$

$\displaystyle V_{rms} = \sqrt{\frac{\omega}{\pi} V_M^2 \left[\frac{1}{2} \cdot \frac{\pi}{\omega} - \frac{1}{4\omega} \sin{(2\omega \cdot \frac{\pi}{\omega})} - \frac{1}{2} \alpha + \frac{1}{4\omega} \sin{2\alpha} \right]}$

$\displaystyle V_{rms} = \sqrt{\frac{\omega}{\pi} V_M^2 \left(\frac{\pi}{2\omega} - \frac{1}{4\omega} \sin{2\pi} - \frac{1}{2\omega} \alpha + \frac{1}{4 \omega} \sin{2\alpha} \right)}$

$\displaystyle V_{rms} = \sqrt{V_M^2 \left(\frac{1}{2} - \frac{1}{2\pi} \alpha + \frac{1}{4\pi} \sin{2\alpha} \right)} = V_M \sqrt{\frac{1}{2} - \frac{1}{2\pi} \alpha + \frac{1}{4\pi} \sin{2\alpha}}$