Problema. La figura muestra un circuito rectificador trifásico de onda completa que alimenta una carga dc. El circuito utiliza SCR en lugar de diodos como elementos de rectificación.
a) ¿Cuáles serán el voltaje rms de la carga y el factor de rizado, si cada SCR se disparatan pronto se polariza directamente? ¿A qué ángulo de fase deben dispararse los SCR para operar de esta forma? Dibuje el voltaje de salida para este caso.
b) ¿Cuáles serán el voltaje rms de la carga y el rizado, si cada SCR se dispara a un ángulo de fase de 90° (esto es, a la mitad del semiciclo en el cual está polarizado positivamente)? Diagrame o dibuje el voltaje de salida para este caso.

Solución. Se asume que los tres voltajes aplicados a este circuito son:
El periodo de la forma de onda de la entrada es , donde
. Para el propósito del cálculo de este problema, se supondrá que
(60 Hz).
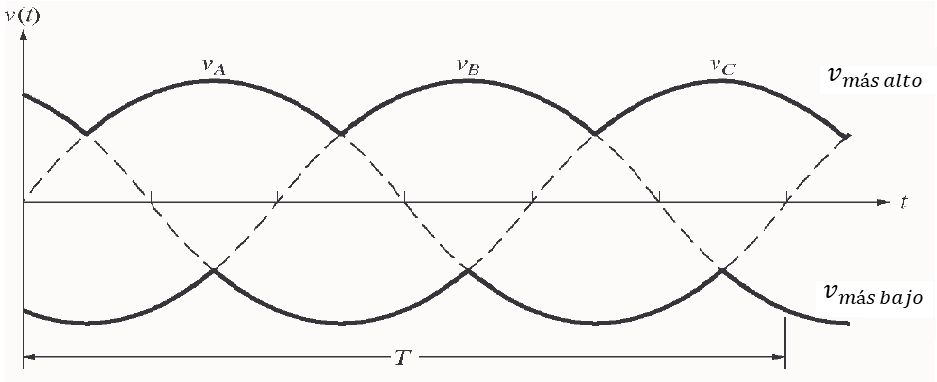
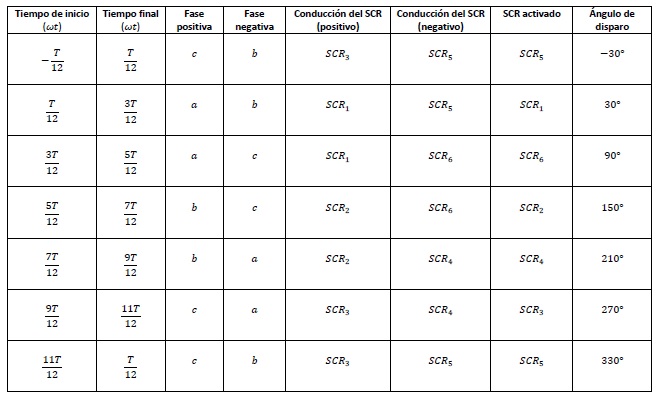
Solución a). Cuando el SCR empiece a conducir tan pronto como estén polarizados directamente, por lo que este circuito es un puente de onda completa trifásico. El diagrama del voltaje de salida es visualizado a continuación, y con un rizado de 4.2%. La siguiente tabla muestra en que orden los SCR deben conducir para crear el voltaje de salida mostrado. Los tiempos son expresados como múltiplos del periodo en la forma de onda de la entrada y el ángulo de disparo está dado en grados con respecto al tiempo cero.
Y la gráfica donde muestra el voltaje de salida es el siguiente
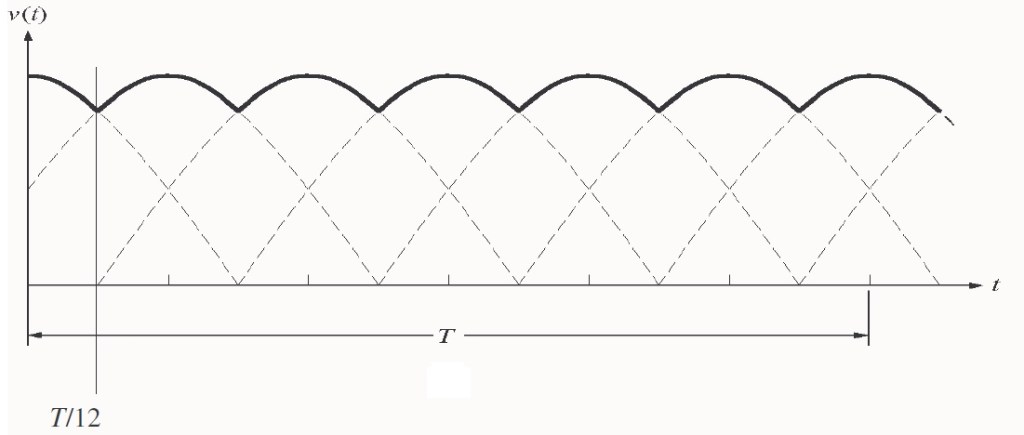
Solución b). Si cada SCR está activado a la mitad de cada semiciclo durante el cuál esta polarizado directamente, los voltajes resultante de fase a, b y c serán cero antes de la primera mitad de cada semiciclo y el valor sinusoidal completo de la segunda mitad de cada semiciclo. Estas formas de ondan se muestran a continuación.
El siguiente programa escrito está basado en MATLAB R2018a y ayuda a simular de un controlador de ángulo de fase ac.
function volts = controlador_bifasico(wt,theta0,fire)
%Función que simula la salida de un controlador de ángulo de fase ac que
%opera simétricamente en semiciclo positivo y negativo. Asume que el
%voltaje pico es VM = 120*sqrt(2) = 170 (V) por conveniencia.
%
%wt = corriente de fase en grados
%theta0 = ángulo de fase inicial en grados
%fire = ángulo de disparo en grados
%Factor de conversión de grados a radianes
deg2rad = pi / 180;
%Elimina las ambigüedades de fase: 0 <= wt < 360 grados
ang = wt + theta0;
while ang >= 360
ang = ang - 360;
end
while ang < 0
ang = ang + 360;
end
%Simula la salida del controlado ángulo de fase
if (ang >= fire & ang <= 180)
volts = 170sin(angdeg2rad);
elseif (ang >=(fire + 180) & ang <= 360)
volts = 170sin(angdeg2rad);
else
volts = 0;
end
Al momento de guardarlo, debe llamarse «controlador_bifasico.m«. Después, es necesario simular el rizado de la forma de onda de la entrada, así que, se escribe el siguiente código
function r = ripple(waveform)
%Funcion para calcular el rizado de la forma de onda de la entrada.
%Calcular el valor promedio de la forma onda
nvals = size(waveform,2);
temp = 0;
for ii = 1:nvals
temp = temp + waveform(ii);
end
promedio = temp/nvals;
%Calculo de los valores rms de la forma de onda.
temp = 0;
for ii = 1:nvals
temp = temp + waveform(ii)^2;
end
rms = sqrt(temp/nvals);
%Cálculo del factor de rizado
r = sqrt((rms/promedio)^2-1) * 100;
Al momento de guardar el segundo archivo, debe llamarse «ripple.m«. Ahora, se realiza un último programa para graficar y calcular los voltajes trifásicos cuando se active cada SCR. El programa que se escribió es el siguiente
%Archivo .m para calcular y graficar los voltajes trifásicos cuando cada
%SCR en el rectificador de onda completa trifásico activos en un ángulo de
%fase de 90 grados.
clear all
%Cálculo de la forma de onda para el tiempo desde 0 hasta 1/30 (s).
t = (0:1/21600:1/30);
deg = zeros(size(t));
rms = zeros(size(t));
va = zeros(size(t));
vb = zeros(size(t));
vc = zeros(size(t));
out = zeros(size(t));
for ii = 1:length(t)
%Obtiene el ángulo equivalente en grados. Note que 1/60s = 360 grados
%para una forma de onda de 60 (Hz).
theta = 21600*t(ii);
%Calcula el voltaje de cada fase en cada ángulo va(ii) = controlador_bifasico(theta,0,90); vb(ii) = controlador_bifasico(theta,-120,90); vc(ii) = controlador_bifasico(theta,120,90);
end
%Cálculo de la salida de voltaje del rectificador
for ii = 1:length(t)
vals = [va(ii) vb(ii) vc(ii)];
out(ii) = max(vals) - min(vals);
end
%Cálculo y visualización del rizado
disp(['El rizado es ' num2str(ripple(out))]);
%Gráfica del voltaje contra el tiempo
figure(1)
plot(t,va,'b','Linewidth',1.0);
hold on;
plot(t,vb,'r:','Linewidth',1.0);
plot(t,vc,'r--','Linewidth',1.0);
title('\bfVoltajes de fase');
xlabel('\bfTiempo (s)');
ylabel('\bfVoltaje (V)');
grid on;
legend('Fase a', 'Fase b', 'Fase c');
hold off;
%Gráfica del voltaje de salida contra el tiempo
figure(2)
plot(t,out,'b','Linewidth',1.0);
title('\bfVoltaje de salida');
xlabel('\bfTiempo (s)');
ylabel('\bfVoltaje (V)');
axis([0 1/30 0 260]);
grid on;
hold off;
Al momento de guardar el tercer programa, puede tener cualquier nombre. Ejecutando este último programa, en la pantalla «Command Window«, muestra el resultado

Y en automático, se muestran las dos gráficas
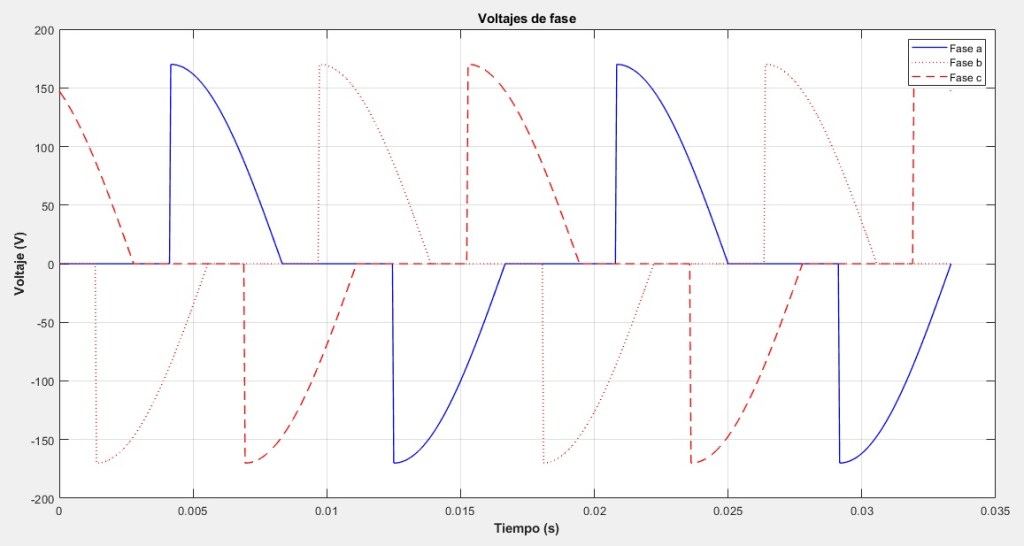
Figura 3.14.6

Figura 3.14.7
Con esto finaliza la solución del inciso b).