El bote. Razón de cambio. Aplicaciones de cálculo diferencial.

Problema 1. Un bote navega paralelamente a una costa rectilínea a una velocidad de 40 km/hr, manteniéndose a una distancia constante de 1.5 km de la costa. Desde un lugar de observación situado a 0.5 km tierra adentro, se dirige un haz de luz de un foco estacionario siguiendo siempre al bote. ¿A qué velocidad en rad/seg y en grados/min habrá de girar el haz de luz para seguir al bote

a) En el momento en que éste pasa al frente del lugar de observación?
b) Cuando lo haya rebasado medio kilómetro?

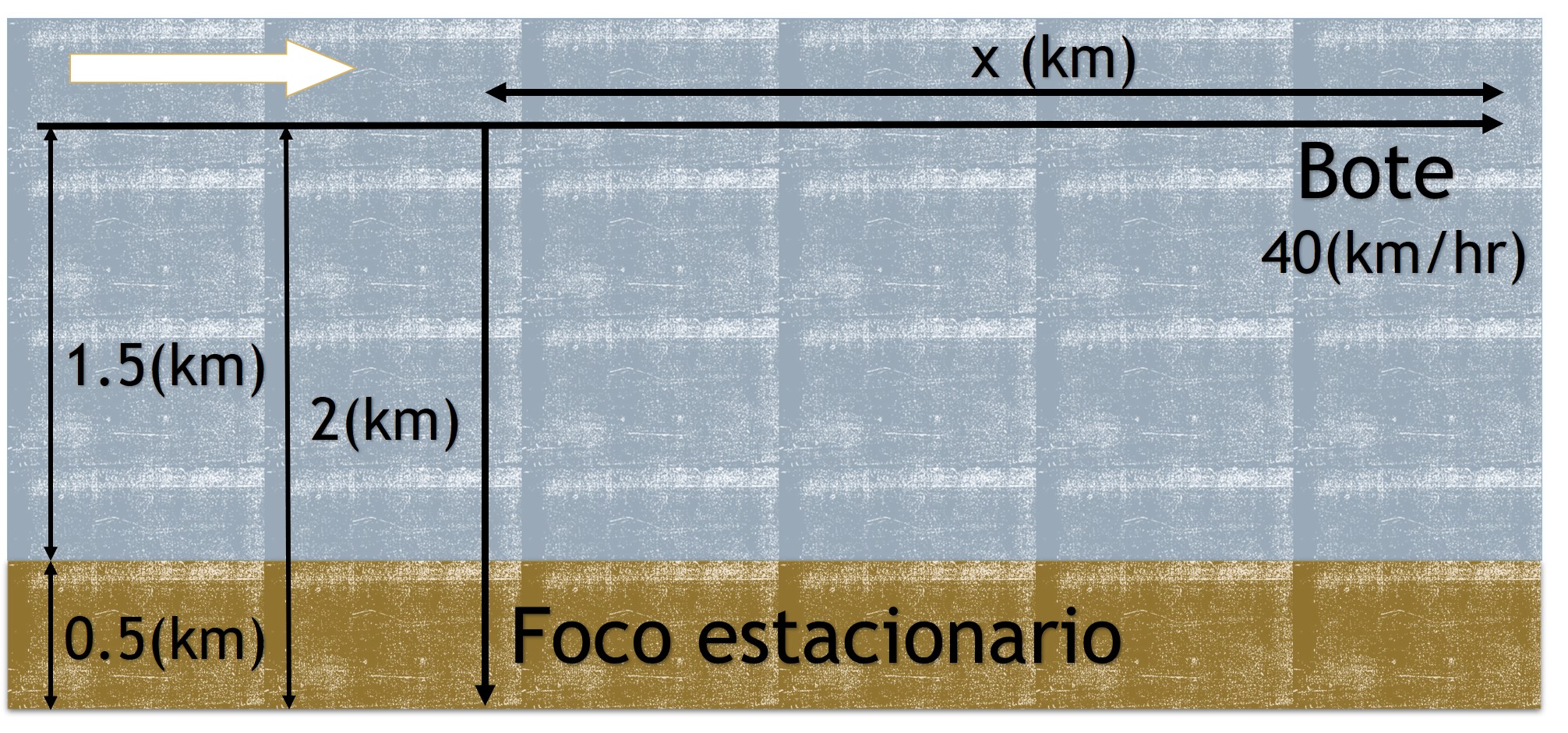
*Figura 3.1.1 Descripción gráfica de la navegación el bote.*

Solución. Primero, se debe obtener la ecuación estática.

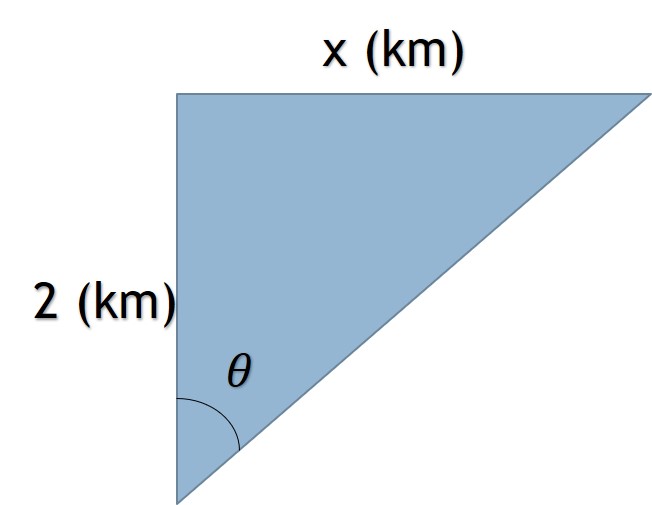
Figura 3.1.2 Triángulo rectángulo de la navegación del bote.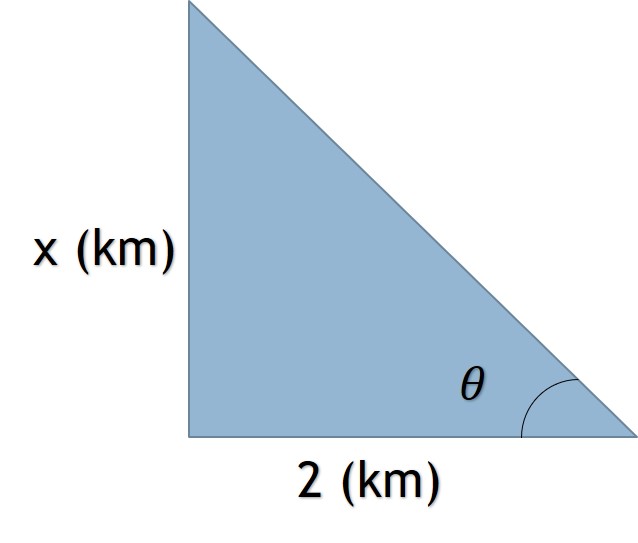
Figura 3.1.3 Giro de 180 grados del triángulo rectángulo.

Usando trigonometría, se observa que

$\displaystyle \tan{\theta} = \frac{x}{2}$

Despejando la variable θ, se tiene que

$\displaystyle \theta = \arctan{\left(\frac{x}{2} \right)}$

Donde esta ecuación es la ecuación estática.

Derivando la ecuación estática con respecto a la variable “ $t$ ”:

$\displaystyle \theta = \arctan{\left(\frac{x}{2} \right)}$

$\displaystyle \frac{d\theta}{dt} = \frac{d}{dt} [\arctan{\left(\frac{x}{2} \right)}]$

$\displaystyle \frac{d\theta}{dt} = \frac{1}{1+(x/2)^2} \cdot \frac{d}{dt} (\frac{x}{2})$

$\displaystyle \frac{d\theta}{dt} = \frac{1}{1+(x/2)^2} (\frac{1}{2}) \cdot \frac{d}{dt}(x)$

$\displaystyle \frac{d\theta}{dt} = \frac{1/2}{1+(x/2)^2} \cdot \frac{dx}{dt}$

Por lo que, este resultado es la ecuación cinemática.

Solución a. Del a), si el bote está frente al lugar de observación, habrá un ángulo de θ=0°, la velocidad del bote es de 40 (km/hr) y la distancia es nula (x = 0 km). Entonces:

$\displaystyle \frac{d\theta}{dt} = \frac{1/2}{1+(x/2)^2} \frac{dx}{dt} = \frac{1/2}{1+(0/2)^2}(40)$

$\displaystyle \frac{d\theta}{dt} = \frac{1/2}{1}(40) = \frac{1}{2} (40)$

$\displaystyle \frac{d\theta}{dt} = 20 \ (rad/hr)$

Para este resultado se hará una conversión de radianes a grados y de horas a minutos.

$\displaystyle \frac{d\theta}{dt} = 20 (rad/hr) = 20(rad/hr)(\frac{1 \ hr}{60 \ min})(\frac{180 \ grados}{\pi \ rad})$

$\displaystyle \frac{d\theta}{dt} = 19.099 \ (grados/min)$

Por lo tanto, el rayo de luz debe girar a razón de 20 (rad/hr) o 19.099 (°/min).

Solución b. Del b), si el bote ha rebasado medio kilómetro, por lo que $x=0.5 \ (km)$ , con la velocidad del bote de dx/dt=40 km/hr, el haz de luz tendrá la siguiente velocidad:

$\displaystyle \frac{d\theta}{dt} = \frac{1/2}{1+(x/2)^2}\ \frac{dx}{dt} = \frac{1/2}{1+(0.5/2)^2} (40)$

$\displaystyle \frac{d\theta}{dt} = \frac{1/2}{1+0.0625}(40)$

$\displaystyle \frac{d\theta}{dt} = 18.8235 \ (rad/hr)$

Para este resultado se hará una conversión de radianes a grados y de horas a minutos.

$\displaystyle \frac{d\theta}{dt} = 18.8235 \ (rad/hr) = 18.8235(rad/hr)(\frac{1 \ hr}{60 \ min})(\frac{180 \ grados}{\pi \ rad})$

$\displaystyle \frac{d\theta}{dt} = 17.9736 \ (grados / min)$

Por lo tanto, el haz de luz debe girar a razón de 18.8235 (rad/hr) o 17.9736 (°/min).

El bote. Razón de cambio. Aplicaciones de cálculo diferencial.

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta

El bote. Razón de cambio. Aplicaciones de cálculo diferencial.

Comparte esto:

Relacionado

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta