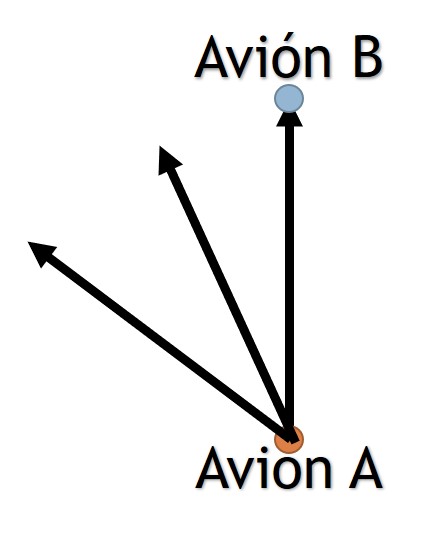
El avión ataca al enemigo. Razón de cambio. Aplicaciones de cálculo diferencial.

Problema. Un avión vuela a una velocidad de 300 (km/hr) en línea recta y en vuelo horizontal, adelanta a un avión enemigo que vuela paralelamente al mismo nivel y en la misma dirección con una velocidad de 250 (km/hr). El ametralladorista del primer avión dirige el tiro sobre el aeroplano enemigo y gira su arma mientras se adelanta. Si las rutas de los dos aeroplanos tienen una separación de 114 (m), hallar la velocidad de giro de la ametralladora:

a) En el momento de adelantar un avión al otro.
b) Cuando ha transcurrido medio minuto después.

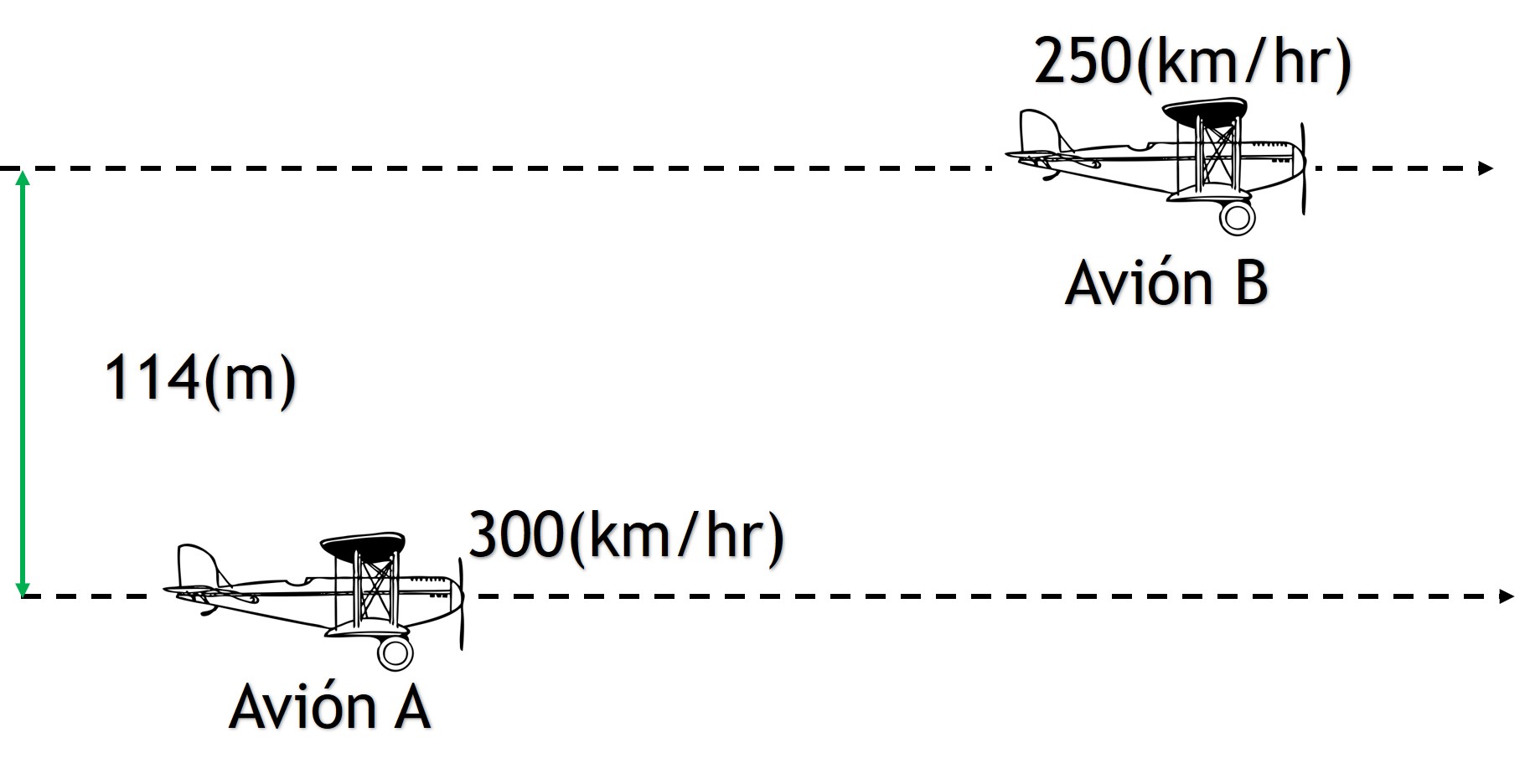
*Figura 3.3.1 Imagen ilustrativa del problema 3.*

Solución a). Se determina la ecuación estática por medio del triángulo rectángulo.

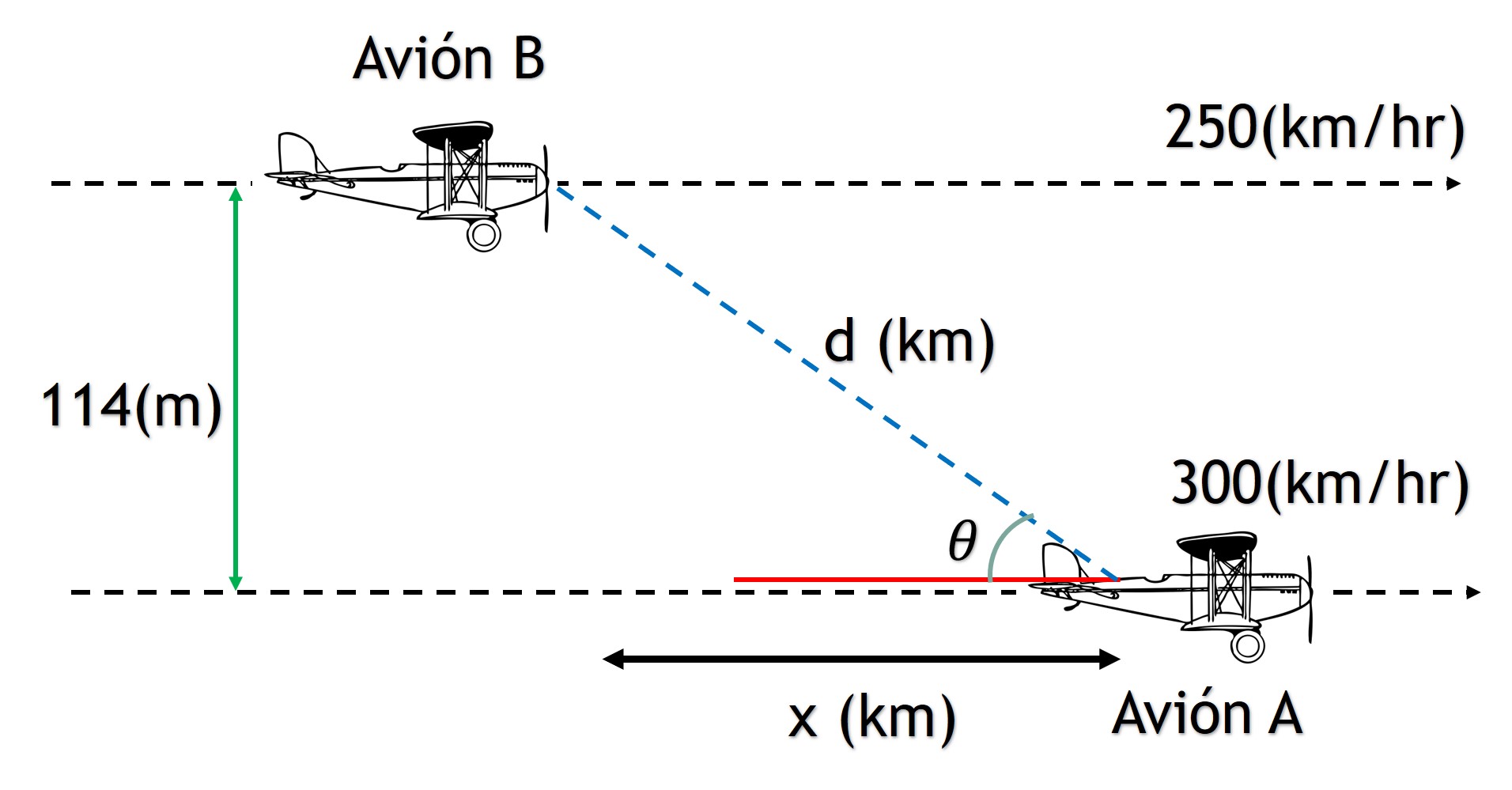
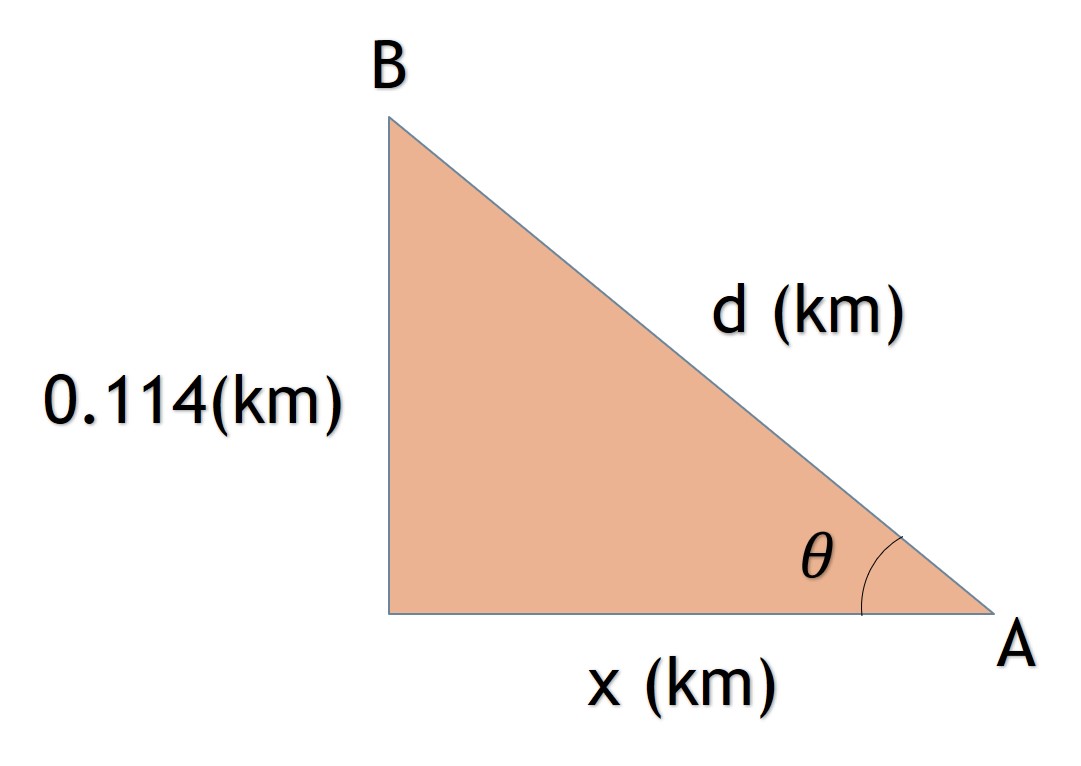
*Figura 3.3.2 Cuando el avión se adelanta del otro.*

*Figura 3.3.3 Triángulo rectángulo del inciso a).*

Utilizando trigonometría

$\displaystyle \tan{\theta} = \frac{0.114}{x}$

Despejando θ

$\displaystyle \theta = \arctan{(\frac{0.114}{x})}$

Este resultado es la ecuación estática.

Se deriva la ecuación estática con respecto a “ $t$ ”:

$\displaystyle \theta = \arctan{(\frac{0.114}{x})}$

$\displaystyle \frac{d\theta}{dt} = \frac{d}{dt} \left[\arctan{(\frac{0.114}{x})} \right]$

$\displaystyle \frac{d\theta}{dt} = \frac{\frac{d}{dt} (\frac{0.114}{x})}{1+(\frac{0.114}{x})^2}$

$\displaystyle \frac{d\theta}{dt} = \frac{- \frac{0.114}{x^2} (\frac{dx}{dt})}{1 + \frac{0.013}{x^2}}$

$\displaystyle \frac{d\theta}{dt} = -\frac{0.114}{x^2+0.013} \ \frac{dx}{dt}$

El término “ $\displaystyle \frac{dx}{dt}$ ” representa la velocidad relativa de los aviones A y B, por lo que

$\displaystyle \frac{dx}{dt} = 50 \ (km/hr)$

*Figura 3.3.4 Posición del avión A cuando está justo sobre el avión B.*

Del a), la velocidad de giro de la ametralladora en el momento de que el avión A adelanta al avión B.

$\displaystyle \frac{d\theta}{dt} = -(\frac{0.114}{x^2+0.013}) \ (\frac{dx}{dt})$

$\displaystyle \frac{d\theta}{dt} = - \left[ \frac{0.114}{(0)^2+0.013} \right](50)$

$\displaystyle \frac{d\theta}{dt} = -438.4615 \ (rad/hr)$

De este último resultado, realizando la conversión de radianes a grados y de horas a minutos:

*Figura 3.3.5 Posición del avión A cuando se adelanta del avión B,*

$\displaystyle \frac{d\theta}{dt} = -438.4615 \ (rad/hr)$

$\displaystyle \frac{d\theta}{dt} = -438.4615 \ (rad/hr)(\frac{180 \ grados}{\pi \ rad})(\frac{1 \ hr}{3600 \ seg})$

$\displaystyle \therefore \frac{d\theta}{dt} = -6.9783 \ (grados/seg)$

Por lo tanto, el ángulo de tiro disminuye a razón de 6.97 (°/seg).

Del b), primero se determina la distancia horizontal que ha avanzado el avión A con respecto al avión B en medio minuto:

$\displaystyle v_x = \frac{dx}{dt} = 50 \ (km/hr)$

$\displaystyle v_x = 50 \ (km/hr) (\frac{1 \ hr}{3600 \ seg}) = 0.0139 \ (km/seg)$

Despejando la distancia horizontal, representado como “ $x$ ”:

$\displaystyle v_x = \frac{x}{t}$

$x = t \ v_x$

$x = (30 seg)(0.0139 km/seg)$

$x=0.417 \ (km)$

La velocidad de giro de la ametralladora, después de medio minuto, es:

$\displaystyle \frac{d\theta}{dt} = -(\frac{0.114}{x^2+0.013})(\frac{dx}{dt})$

$\displaystyle {d\theta}{dt} = - \left[ \frac{0.114}{(0.417)^2+0.013} \right](50 \ km/hr)$

$\displaystyle \frac{d\theta}{dt} = -30.499 \ (rad/hr)$

$\displaystyle \frac{d\theta}{dt} = (-30.499 \ rad/hr) \left(\frac{1 \ hr}{3600 \ seg} \right) \left( \frac{180 \ grados}{\pi \ rad} \right)$

$\displaystyle \therefore \frac{d\theta}{dt} = -0.485$ (°/seg)

Por lo tanto, después de medio minuto, la ametralladora disminuirá su velocidad de giro a 0.485 (°/seg).

El avión ataca al enemigo. Razón de cambio. Aplicaciones de cálculo diferencial.

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta

El avión ataca al enemigo. Razón de cambio. Aplicaciones de cálculo diferencial.

Comparte esto:

Relacionado

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta