La escalera y la pared. Razón de cambio. Aplicaciones de cálculo diferencial.

Problema. Una escalera de 10 (m) de longitud sobre un piso horizontal está recostada contra una pared vertical. Su pie se resbala a una velocidad constante de 2 (m/seg) alejándose de la pared.

a) ¿A qué velocidad baja la parte superior de la escalera cuando el pie dista 4 (m) de la pared?
b) ¿A qué velocidad varía en ese mismo instante el ángulo de la escalera con la horizontal?
c) ¿En que momento los dos extremos se mueven a la misma velocidad?

*Figura 3.4.1 Imagen ilustrativa del problema 4.*

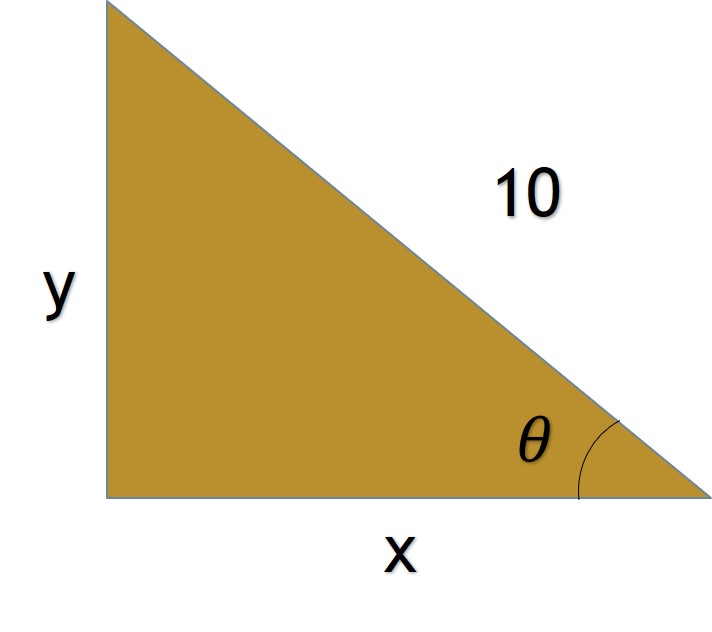
Solución. Por trigonometría, se toma el término cos θ:

$\displaystyle \cos{\theta} = \frac{x}{10}$

Despejando θ:

$\displaystyle \cos{\theta} = \frac{x}{10}$

$\displaystyle \theta = \arccos{(\frac{x}{10})}$

Por lo que, este despeje representa la primera ecuación estática. Para obtener la segunda ecuación se utiliza el teorema de Pitágoras.

$x^2 + y^2 = 10^2$

$x^2 + y^2 = 100$

Y esta es la segunda ecuación estática.

En la primera ecuación estática se deriva en ambos miembros con respecto a “ $t$ ”:

$\displaystyle \theta = \arccos{(\frac{x}{10})}$

$\displaystyle \frac{d\theta}{dt} = \frac{d}{dt} \left[\arccos{(\frac{x}{10})} \right]$

$\displaystyle \frac{d\theta}{dt} = -\frac{\frac{d}{dt} (\frac{x}{10})}{\sqrt{1-(\frac{x}{10})^2}}$

$\displaystyle \frac{d\theta}{dt} = -\frac{1}{\sqrt{100-x^2}} (\frac{dx}{dt})$

Esta es la primera ecuación cinemática.

Derivando en ambos miembros:

$\displaystyle \frac{d}{dt} (x^2) + \frac{d}{dt} (y^2) = \frac{d}{dt} (10)$

$\displaystyle 2x \frac{dx}{dt} + 2y \frac{dy}{dt} = 0$

$\displaystyle x \frac{dx}{dt} + y \frac{dy}{dt} = 0$

$\displaystyle x \frac{dx}{dt} =-y \frac{dy}{dt}$

Esta expresión representa la segunda ecuación cinemática.

Solución a). Del a), cuando el pie dista 4 (m) de la pared, se calcula la altura despejando (en la segunda ecuación estática) la variable “ $y$ ”:

$x^2+y^2=100$

$\displaystyle y = \sqrt{100-x^2}$

Si $x=4$ :

$\displaystyle y= \sqrt{100-4^2}$

$\displaystyle y = \sqrt{100-16}$

$\displaystyle y=\sqrt{84}$

De la segunda ecuación cinemática

$\displaystyle x \frac{dx}{dt}=-y \frac{dy}{dt}$

Se despeja “ $dy/dt$ ” para obtener la velocidad en el eje vertical

$\displaystyle x \frac{dx}{dt} = -y \frac{dy}{dt}$

$\displaystyle \frac{dy}{dt} = -\frac{x}{y} (\frac{dx}{dt})$

Para calcular el resultado del a), sustituyendo los siguientes datos $\displaystyle \frac{dx}{dt} = 2$ , $x=4$ , y $\displaystyle y=\sqrt{84}$ :

$\displaystyle \frac{dy}{dt} = -\frac{x}{y} (\frac{dx}{dt})$

$\displaystyle \frac{dy}{dt} = -\frac{4}{\sqrt{84}} (2)$

$\displaystyle \frac{dy}{dt} = -0,87 \ (m/seg)$

Por lo tanto, en el extremo superior de la escalera desciende a razón de 0.87 (m/seg).

Solución b). Del b), para obtener el valor de la velocidad en que varía el ángulo con respecto a la horizontal, se utiliza la primera ecuación cinemática:

$\displaystyle \frac{d\theta}{dt} = -\frac{1}{\sqrt{100-x^2}} (\frac{dx}{dt})$

Para obtener el resultado deseado, sustituyendo $\displaystyle \frac{dx}{dt} = 2$ y $x=4$ :

$\displaystyle \frac{d\theta}{dt} = -\frac{1}{\sqrt{100-x^2}} (\frac{dx}{dt})$

$\displaystyle \frac{d\theta}{dt} = -\frac{1}{\sqrt{100-(4)^2}} (2)$