Problema. Una lámina metálica en forma de triángulo equilátero se calienta y en cada lado se dilata a una velocidad de 1 (cm/hr). ¿A qué velocidad se dilata el área cuando los lados miden 40 (cm)?

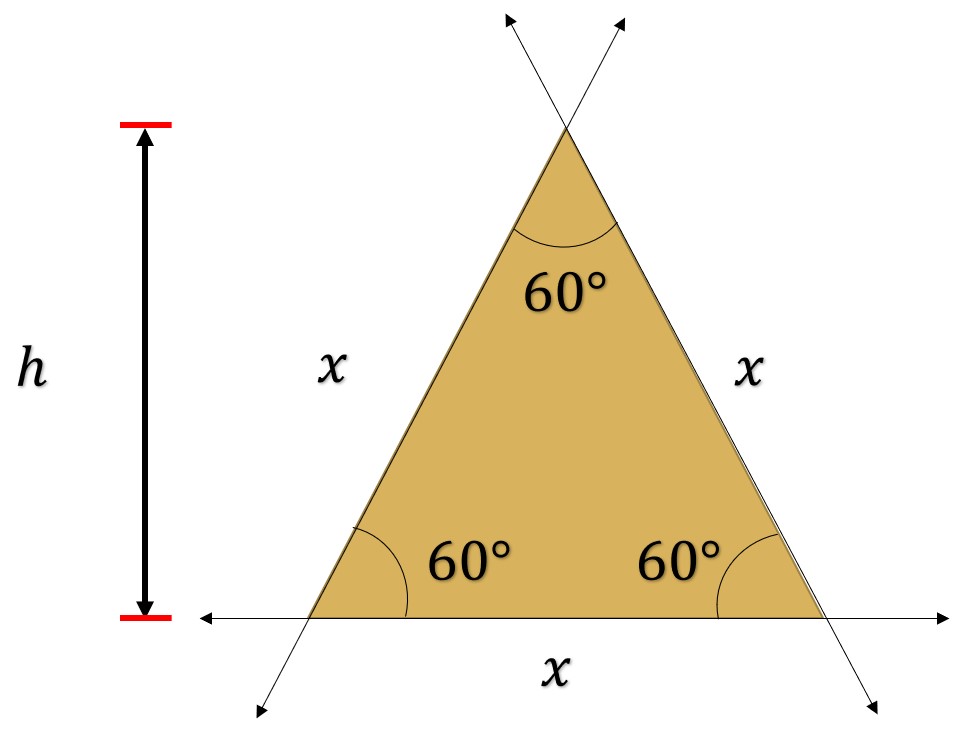
Figura 3.9.1 Representación gráfica del problema.

Solución. Se sabe que el área de un triángulo es

\displaystyle A = \frac{1}{2} bh

Si b=x

\displaystyle A = \frac{1}{2} bh

\displaystyle A = \frac{1}{2}xh

Al dividir a la mitad el triángulo equilátero, se observa lo siguiente

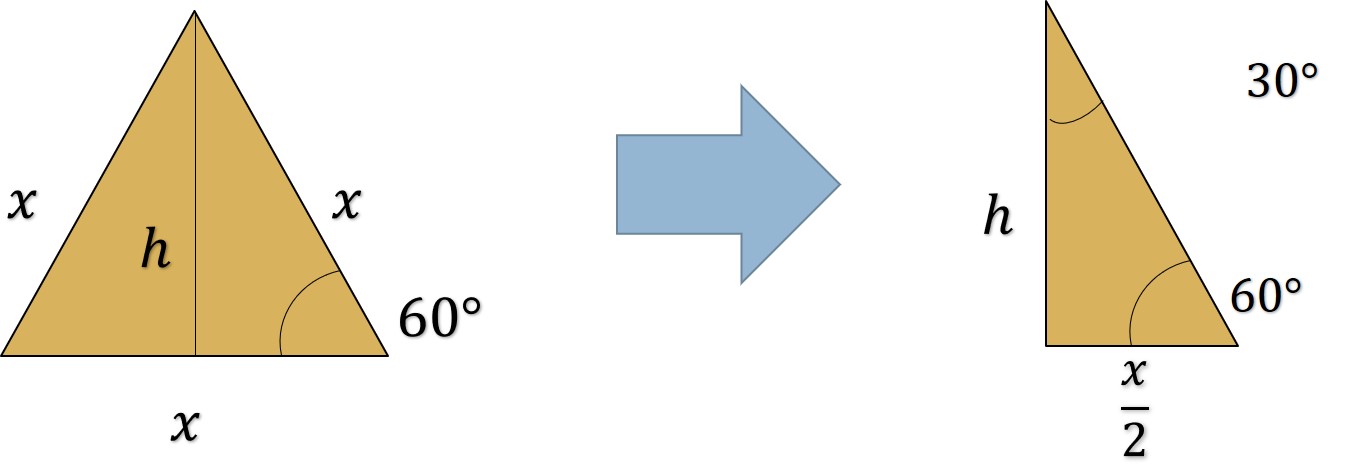
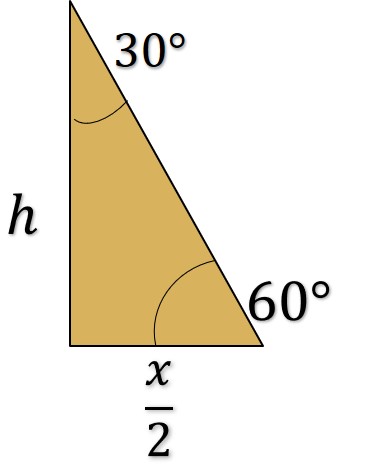
Figura 3.9.2 Dividiendo el triángulo equilátero en dos partes.
Figura 3.9.3 Análisis trigonométrico del triángulo rectángulo.

Aplicando trigonometría en el triángulo rectángulo

\displaystyle \tan{60} = \frac{h}{\frac{x}{2}}

\displaystyle \frac{x}{2} (\tan{60}) = h

\displaystyle h = \frac{x}{2} \tan{60}

\displaystyle h = \left(\frac{\tan{60}}{2} \right) x

\displaystyle h = \frac{\sqrt{3}}{2} x

Sustituyendo este resultado con la ecuación del área del triángulo

\displaystyle A = \frac{1}{2} xh

\displaystyle A = \frac{1}{2} x \left(\frac{\sqrt{3}}{2} x \right)

\displaystyle A = \frac{\sqrt{3}}{4} x^2

La cual, representa la ecuación estática.

Derivando en ambos miembros con respecto a “t”

\displaystyle \frac{dA}{dt} = \frac{d}{dt} (\frac{\sqrt{3}}{4} x^2)

\displaystyle \frac{dA}{dt} = \frac{\sqrt{3}}{4} \frac{d}{dt} (x^2)

\displaystyle \frac{dA}{dt} = \frac{\sqrt{3}}{4} (2x) \frac{dx}{dt}

\displaystyle \frac{dA}{dt} = \frac{2 \sqrt{3}}{4} x \frac{dx}{dt}

\displaystyle \frac{dA}{dt} = \frac{\sqrt{3}}{2} x \frac{dx}{dt}

Donde, esta ecuación representa la ecuación cinemática.

Para obtener el resultado requerido, se sabe que x=40 y \displaystyle \frac{dx}{dt}=1, entonces

\displaystyle \frac{dA}{dt} = \frac{\sqrt{3}}{2} x \frac{dx}{dt}

\displaystyle \frac{dA}{dt} = \frac{\sqrt{3}}{2} (40)(1)

\displaystyle \frac{dA}{dt} = 20\sqrt{3} \approx 34.641 \ (cm^2/hr)

Por lo tanto, el área de la lámina metálica en forma triangular aumenta a razón de 34.641 (cm^2/hr).

Avatar de Desconocido

Publicado por Cesar Reyes

Dedicado a compartir información temas referentes al cálculo básicos, intermedios y avanzados mediante presentaciones PDF, videos y publicaciones en este sitio web.

Deja un comentario

Este sitio utiliza Akismet para reducir el spam. Conoce cómo se procesan los datos de tus comentarios.