Reloj de arena. Razón de cambio. Aplicaciones del cálculo diferencial.

Problema. Hay un reloj de arena cuyo cono inferior tiene en un momento dado 60 (cm) de altura y 30 (cm) de radio en la base. Al voltearlo, la arena desciende a velocidad constante de 1 ( $cm^3/min$ ). ¿A qué velocidad sube el nivel en el cono inferior si suponiendo que la superficie es plana y horizontal cuando la altura de la área es de 20 (cm)?

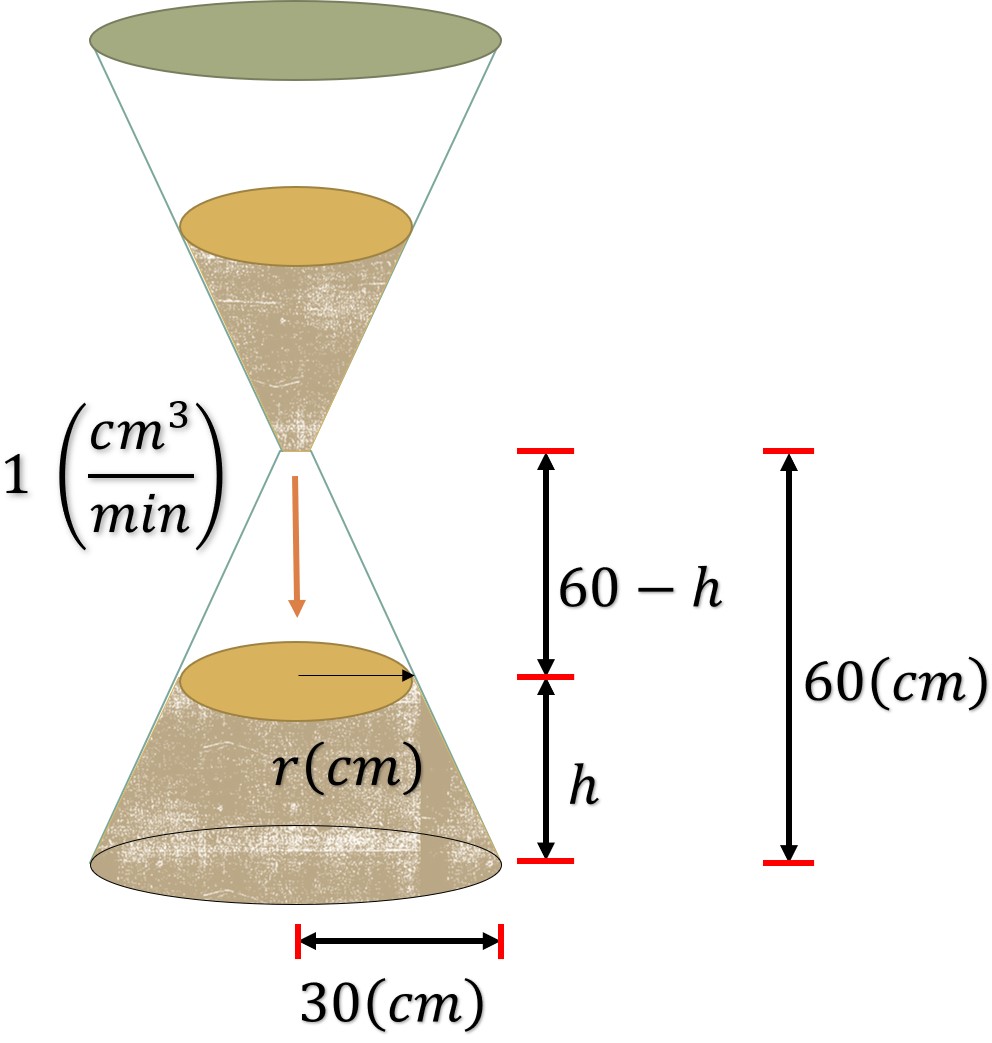
Solución. Utilizando la ecuación del volumen del tronco de cono formado por la arena

$\displaystyle V = \frac{1}{3} h(B_1 + B_2 + \sqrt{B_1 B_2})$

Para determinar la base mayor, se sabe que $r_1=30$ , entonces

$B_1 = \pi r_1^2$

$B_1 = \pi (30)^2$

$B_1 = 900 \pi$

Y en el caso de la base menor, $r_2=r$

$B_2 = \pi r_2^2$

$B_2 = \pi r^2$

Sustituyendo estos parámetros en la ecuación del volumen del tronco

$\displaystyle V = \frac{1}{3} h (B_1 + B_2 + \sqrt{B_1 B_2})$

$\displaystyle V = \frac{1}{3} h(900 \pi + \pi r^2 + \sqrt{(900 \pi)(\pi r^2)}$

$\displaystyle V = \frac{1}{3} h(900 \pi + \pi r^2 + \sqrt{900\pi^2 r^2})$

$\displaystyle V = \frac{1}{3} h(900\pi + \pi r^2 + 30\pi r)$

$\displaystyle V = \frac{1}{3} \pi h(900 + r^2 + 30r)$

$\displaystyle V = \frac{1}{3} \pi h(r^2 + 30r + 900)$

Del cono inferior se observa lo siguiente

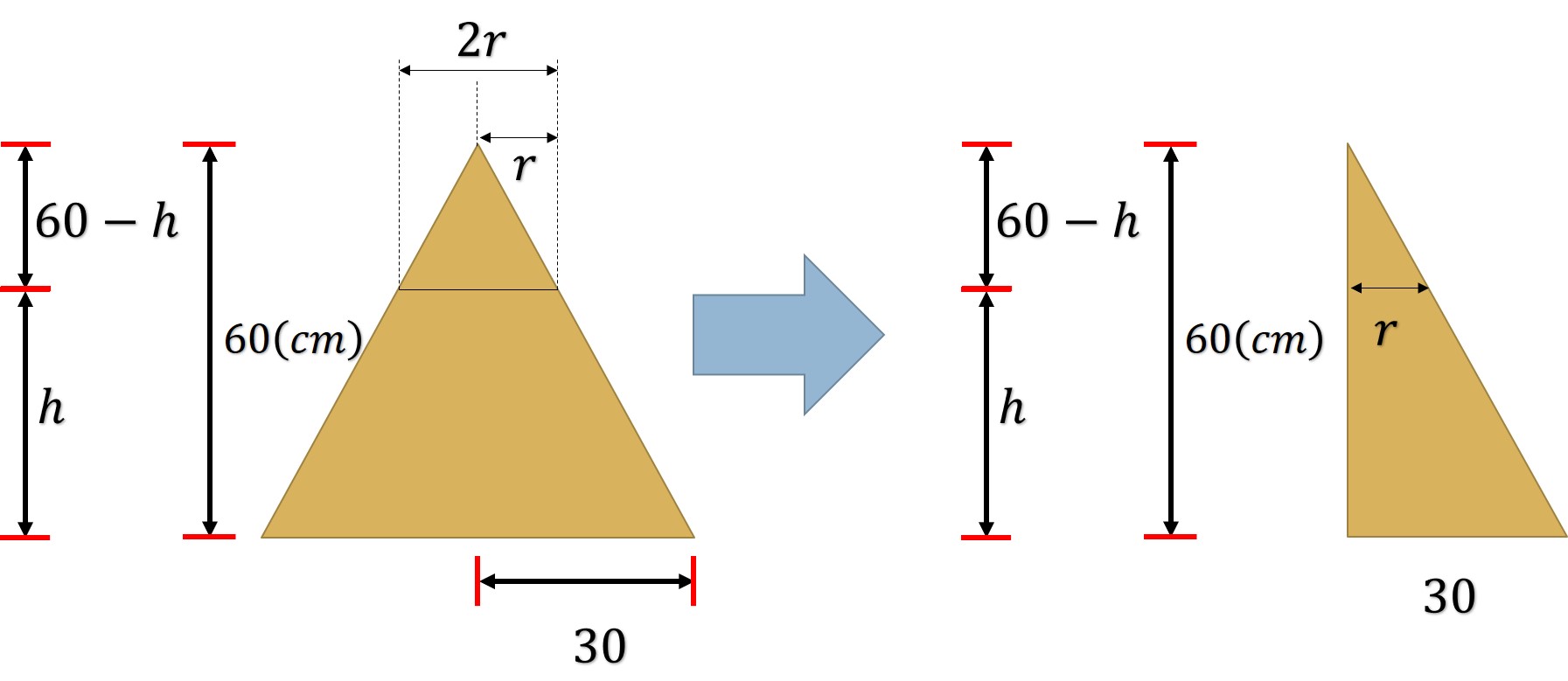
Por triángulos semejantes

$\displaystyle \frac{60}{30} = \frac{60-h}{r}$

$\displaystyle 2 = \frac{60-h}{r}$

$\displaystyle r = \frac{60-h}{2}$

Sustituyendo en la ecuación del volumen del tronco de cono

$\displaystyle V = \frac{1}{3} \pi h(r^2+30r+900)$

$\displaystyle V = \frac{1}{3} \pi h \left[(\frac{60-h}{2})^2 + 30(\frac{60-h}{2}) + 900 \right]$

$\displaystyle V = \frac{1}{3} \pi h(\frac{3600-120h+h^2}{4} + \frac{1800-30h}{2} + 900)$

$\displaystyle V = \frac{1}{3} \pi h(900 - 30h + \frac{h^2}{4} + 900 - 15h + 900)$

$\displaystyle V = \frac{1}{3} \pi h(\frac{h^2}{4} - 45h + 2700)$

$\displaystyle V = \frac{1}{3} \pi (\frac{h^3}{4} - 45h^2 + 2700h)$

Esto representa la ecuación estática.

Ahora, derivando en ambos miembros con respecto a “ $x$ ”

$\displaystyle \frac{dV}{dt} = \frac{d}{dt} \left[\frac{1}{3} \pi (\frac{h^3}{4} - 45h^2 + 2700h) \right]$

$\displaystyle \frac{dV}{dt} = (\frac{1}{3} \pi) \frac{d}{dt} (\frac{h^3}{4} - 45h^2 + 2700h)$

$\displaystyle \frac{dV}{dt} = (\frac{1}{3} \pi) \left[\frac{1}{4} \frac{d}{dt} (h^3) - 45 \frac{d}{dt} (h^2) + 2700 \frac{d}{dt} (h) \right]$

$\displaystyle \frac{dV}{dt} = (\frac{1}{3} \pi) \left[\frac{1}{4} (3h^2) \frac{dh}{dt} - 45(2h) \frac{dh}{dt} + 2700 \frac{dh}{dt} \right]$

$\displaystyle \frac{dV}{dt} = (\frac{1}{3} \pi)(\frac{3}{4} h^2 \frac{dh}{dt} - 90h \frac{dh}{dt} + 2700 \frac{dh}{dt})$

$\displaystyle \frac{dV}{dt} = (\frac{1}{3} \pi)(\frac{3}{4} h^2 - 90h + 2700) \frac{dh}{dt}$

Despejando “ $\displaystyle dh/dt$ ”

$\displaystyle \frac{dV}{dt} = (\frac{1}{3} \pi)(\frac{3}{4} h^2 - 90h + 2700) \frac{dh}{dt}$

$\displaystyle \frac{\frac{dV}{dt}}{\frac{1}{3} \pi (\frac{3}{4} h^2 - 90h + 2700)} = \frac{dh}{dt}$

$\displaystyle \frac{dh}{dt} = \frac{\frac{dV}{dt}}{\frac{1}{3} \pi (\frac{3}{4} h^2 - 90h + 2700)}$

Y esto es la ecuación cinemática. Para obtener el resultado deseado, se sabe que los datos son $\displaystyle \frac{dV}{dt} = 1$ y $h=20$ . Entonces

$\displaystyle \frac{dh}{dt} = \frac{\frac{dV}{dt}}{\frac{1}{3} \pi (\frac{3}{4} h^2 - 90h + 2700)}$

$\displaystyle \frac{dh}{dt} = \frac{1}{(\frac{1}{3} \pi)[\frac{3}{4} (20)^2 - 90(20) + 2700]}$

$\displaystyle \therefore \frac{dh}{dt} = \frac{1}{400 \pi} \approx 7.95 \times 10^{-4} \ (cm / min)$

Por lo tanto, el nivel de la área sube a razón de 7.95×10^(-4) (cm/min).

Reloj de arena. Razón de cambio. Aplicaciones del cálculo diferencial.

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta

Reloj de arena. Razón de cambio. Aplicaciones del cálculo diferencial.

Comparte esto:

Relacionado

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta