Los brazos de un puente. Razón de cambio. Aplicaciones de cálculo diferencial.

Problema. Los brazos de un puente levadizo giran hacia arriba alrededor de un eje común. La longitud del brazo más corto es de 3 (m) y la del brazo más largo es de 4 (m) y giran a la misma velocidad de 5 (rad/min). Hallar a qué velocidad se acercan o separan las dos extremidades cuando ambos marcan un ángulo de 45° con la horizontal.

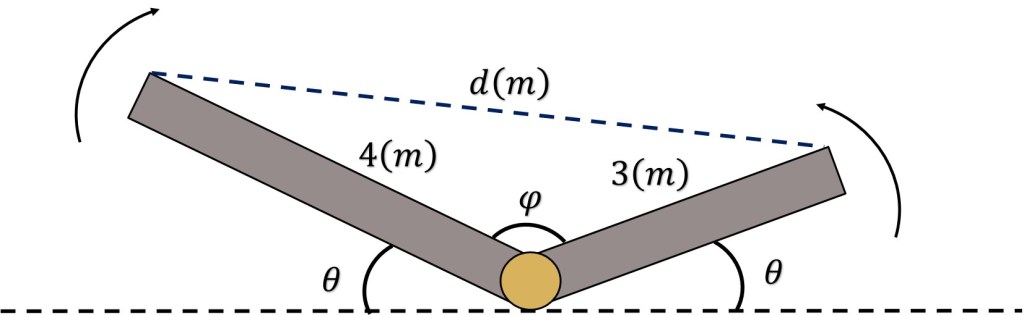
*Figura 3.11.1 Representación gráfica de los brazos de un puente levadizo.*

Solución. Utilizando el triángulo obtuso, se toma la ley de los cosenos para desarrollar la distancia.

*Figura 3.11.2 Triángulo obtuso que representa el análisis de los brazos del puente.*

$d^2=4^2+3^2-2(4)(3) \cos{\phi}$

$d^2=16+9-24 \cos{\phi}$

$\displaystyle d^2=25-24 \cos{\phi}$

$\displaystyle d = \sqrt{25-24 \cos{\phi}}$

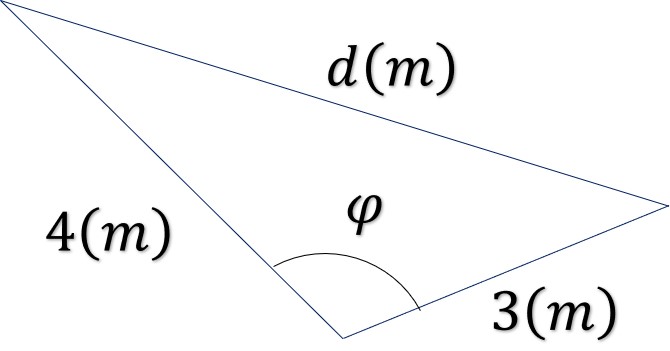
Esta expresión representa la primera ecuación estática.

Analizando los ángulos que forman el par de brazos de 3 (m) y 4 (m), se observa que, por medio de ángulos suplementarios

$\theta + \phi + \theta = 180$ °

$2\theta + \phi = 180$ °

*Figura 3.11.3 Ángulos complementarios.*

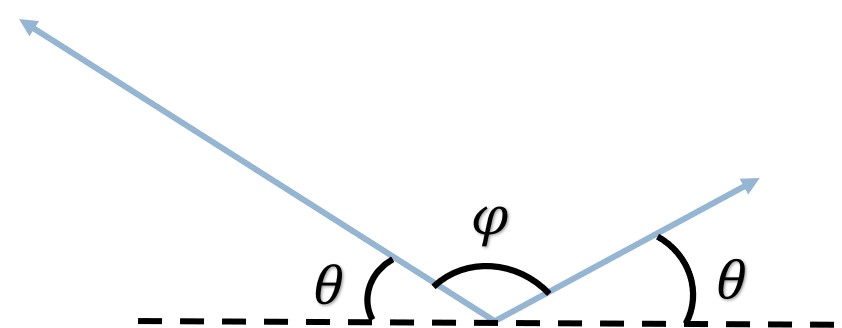
Despejando φ

$2\theta + \phi = 180$ °

$\phi = 180 - 2\theta$

Y esta es la segunda ecuación estática.

De la primera ecuación estática, derivando en ambos miembros con respecto a “ $t$ ”

$\displaystyle d = \sqrt{25-24 \cos{\phi}}$

$\displaystyle \frac{dd}{dt} = \frac{d}{dt} (\sqrt{25-24 \cos{\phi}})$

$\displaystyle \frac{dd}{dt} = \frac{1}{2 \sqrt{25-24 \cos{\phi}}} \frac{d}{dt} (25 - 24 \cos{\phi})$

$\displaystyle \frac{dd}{dt} = \frac{1}{2 \sqrt{25-24 \cos{\phi}}} (24 \sin{\phi}) \frac{d\phi}{dt}$

$\displaystyle \frac{dd}{dt} = \frac{24 \sin{\phi}}{2 \sqrt{25 - 24 \cos{\phi}}} \frac{d\phi}{dt}$

$\displaystyle \frac{dd}{dt} = \frac{12 \sin{\phi}}{\sqrt{25 - 24 \cos{\phi}}} \frac{d\phi}{dt}$

De la segunda ecuación estática, derivando en ambos miembros con respecto a “ $t$ ”

$\phi = 180 - 2\theta$

$\displaystyle \frac{d\phi}{dt} = \frac{d}{dt} (180 - 2\theta)$

$\displaystyle \frac{d\phi}{dt} = \frac{d}{dt} (180) - 2 \frac{d}{dt} (\theta)$

$\displaystyle \frac{d\phi}{dt} = -2 \frac{d\theta}{dt}$

Y esta es la segunda ecuación cinemática.

El problema menciona que los brazos marcan un ángulo de 45°, entonces, θ=45°. Luego

$\phi = 180 - 2\theta$

$\phi = 180 - 2(45)$

$\phi = 90$ °

Por medio de la segunda ecuación cinemática, si $\displaystyle \frac{d\theta}{dt} = 5$ , se obtiene que

$\displaystyle \frac{d\phi}{dt} = -2 \frac{d\theta}{dt}$

$\displaystyle \frac{d\phi}{dt} = -2(5)$

$\displaystyle \frac{d\phi}{dt} = -10 \ (rad/min)$

De la primera ecuación cinemática, se toman los valores siguientes φ=90° y $\displaystyle \frac{d\phi}{dt} = -5$ , por lo que, el resultado es el siguiente.

$\displaystyle \frac{dd}{dt} = \frac{12 \sin{\phi}}{\sqrt{25-24 \cos{\phi}}} \frac{d\phi}{dt}$

$\displaystyle \frac{dd}{dt} = \frac{(12 \sin{90})}{\sqrt{25-24 \cos{90}}} (-5)$

$\displaystyle \therefore \frac{dd}{dt} = -24 \ (m/min)$

Por lo tanto, los extremos de los brazos se aproximan entre sí (uno al otro) a razón de 24 (m/min).

Los brazos de un puente. Razón de cambio. Aplicaciones de cálculo diferencial.

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta

Los brazos de un puente. Razón de cambio. Aplicaciones de cálculo diferencial.

Comparte esto:

Relacionado

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta