Contruyendo una caja. Máximos y mínimos. Aplicaciones de cálculo diferencial.

Problema. Se desea construir una caja de base cuadrada y abierta por la parte superior, utilizando para ello una lámina metálica cuadrada de 1.20 (m) de lado, recortando un cuadrado pequeño en cada esquina y doblando los bordes hacia arriba. Determinar la longitud de los lados para obtener una caja de volumen máximo.

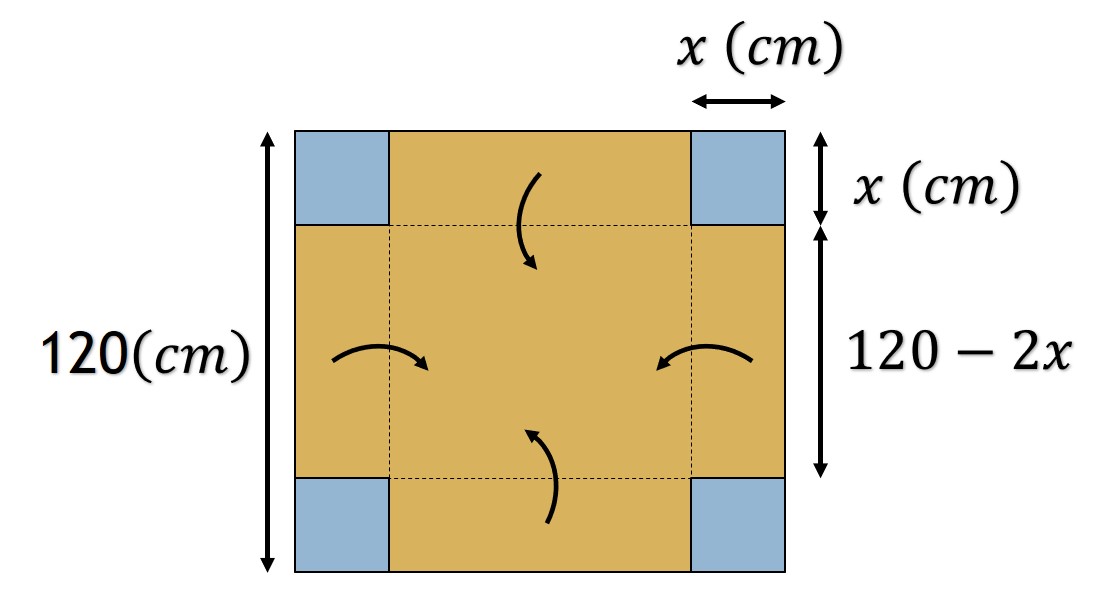
*Figura 4.3.1 Figura ilustrativa del problema.*

Solución. Construyendo la caja, se observa que

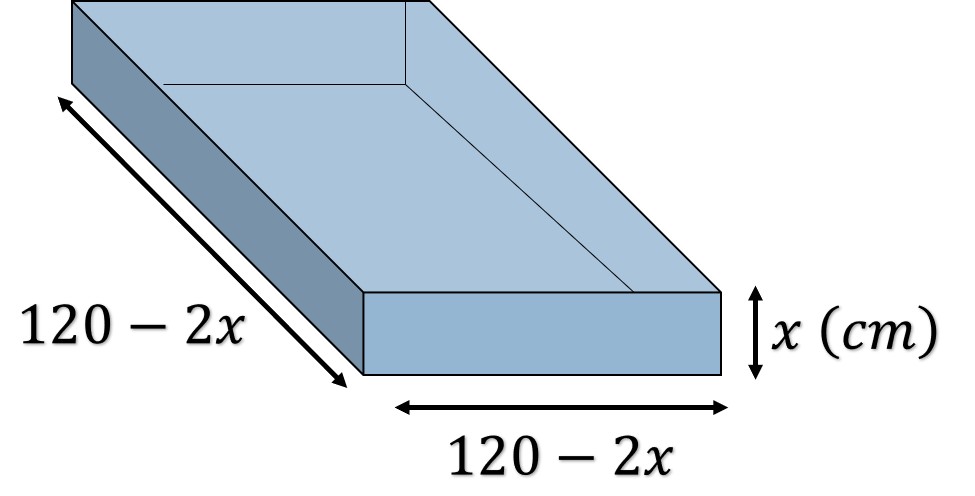
Paso 1. El volumen de la caja es

$V = (\mathrm{base}) (\mathrm{altura})$

$V = (120-2x)(120-2x)(x)$

$V = (2)(60-x)(120-2x)(x)$

$V = (2)(60-x)(2)(60-x)(x)$

$V = 4x(3600-120x+x^2) = 4x(x^2-120x+3600)$

$V = 4x^3 - 480x^2 + 14400x$

Paso 2. Derivando la ecuación del volumen con respecto a “ $x$ ”

$\displaystyle \frac{dV}{dx} = \frac{d}{dx} (4x^3 - 480x^2 + 14400x)$

$\displaystyle \frac{dV}{dx} = 4 \frac{d}{dx} (x^3) - 480 \frac{d}{dx} (x^2) + 14400 \frac{d}{dx} (x)$

$\displaystyle \frac{dV}{dx} = 4(3x^2) - 480(2x) + 14400(1)$

$\displaystyle \frac{dV}{dx} = 12x^2 - 960x + 14400$

Paso 3. Si “ $\displaystyle \frac{dV}{dx}$ ” es nulo

$\displaystyle \frac{dV}{dx} = 12x^2 - 960x + 14400$

$\displaystyle 0 = 12x^2 - 960x + 14400$

$12x^2 - 960x + 14400 = 0$

$\displaystyle \frac{1}{12} (12x^2 - 960x + 14400) = \frac{1}{12} (0)$

$x^2-80x+1200=0$

Utilizando la fórmula general

$\displaystyle x = \frac{-b \pm \sqrt{b^2-4ac}}{2a}$

$\displaystyle x = \frac{-(-80) \pm \sqrt{(-80)^2-4(1)(1200)}}{2(1)}$

$\displaystyle x =\frac{80 \pm \sqrt{6400-4800}}{2}$

$\displaystyle x = \frac{80 \pm \sqrt{1600}}{2}$

$\displaystyle x = \frac{80 \pm 40}{2}$

$x=60 \ \mathrm{y} \ x=20$

No se toma el valor de “ $x=60$ ” debido a que la ecuación “ $120-2x$ ” tendrá un resultado negativo, por lo que, solo se considera el valor de “ $x=20$ ”. Así que la altura es

$\mathrm{altura} = x = 20 \ (cm)$

Y el ancho es

$\mathrm{ancho} = 120 - 2x = 120 - 2(20) = 80 \ (cm)$

Entonces, el volumen es

$V=4x^3-480x^2+14400x$

$V=4(20)^3-480(20)^2+14400(20)$

$\therefore V=128,000(cm^3 )$

Derivando la función nuevamente

$\displaystyle \frac{d}{dx} \left(\frac{dV}{dx} \right) = \frac{d}{dx} (12x^2 - 960x + 14400)$

$\displaystyle \frac{d^2 V}{dx^2} = 12 \frac{d}{dx} (x^2) - 960 \frac{d}{dx} (x) + \frac{d}{dx} (14400)$

$\displaystyle \frac{d^2 V}{dx^2} = 12(2x) - 960(1) + 0$

$\displaystyle \frac{d^2 V}{dx^2} = 24x - 960$

Con “ $x=20$ ”

$\displaystyle \frac{d^2 V}{dx^2} = 24(20) - 960 = -480$

Como $\displaystyle \frac{d^2 V}{dx^2}<0$ se trata de un máximo. Por lo tanto, la caja tendrá un volumen máximo cuando sus bases sean de 80 (cm) y una altura de 20 (cm). El volumen máximo será de 128,000 ( $cm^3$ ).