La suma de dos números es… . Máximos y mínimos. Aplicaciones de cálculo diferencial.

Problema. La suma de dos números enteros es 10. Calcular los dos números de tal manera que la raíz cuadrada de su producto sea máxima.

Solución.

Paso 1. Sean los números “ $x$ ” e “ $y$ ”. Al expresarlo en una suma, su resultado debe de ser 10. Entonces

$x + y = 10$

Despejando “ $y$ ”

$x+y=10$

$y=10-x$

Paso 2. El producto es (asignando a $P$ , que represente ese producto)

$P=xy$

Y para la raíz cuadrada (asignando a $R$ , que represente la raíz cuadrada)

$\displaystyle R = \sqrt{xy}$

Sustituyendo el equivalente de “ $y$ ” (despejado de la ecuación suma) en la ecuación $R$

$\displaystyle R = \sqrt{xy}$

$\displaystyle R = \sqrt{x(10-x)}$

$\displaystyle R = \sqrt{10x - x^2}$

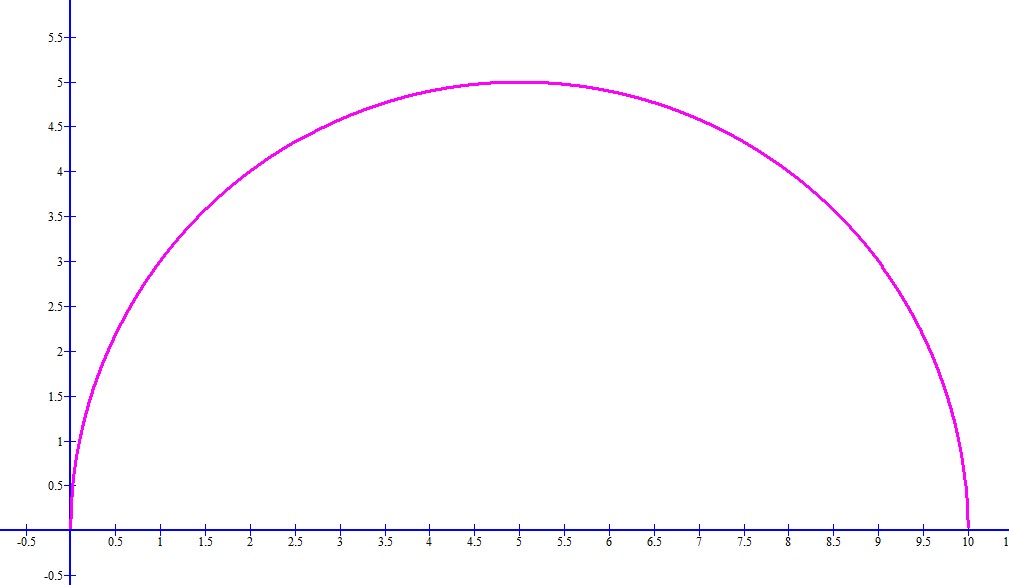
Donde esto representa una parábola fuera del origen con interceptos de $x=0$ y $x=10$ .

*Representación gráfica de la función “ $R=\sqrt{10x - x^2}$ ”.*

*Representación gráfica de la función “ $R=\sqrt{10x - x^2}$ ”.*

Paso 3. Derivando la función $R$ con respecto a “ $x$ ” en ambos miembros

$\displaystyle \frac{dR}{dx} = \frac{d}{dx} \left(\sqrt{10x-x^2} \right)$

$\displaystyle \frac{dR}{dx} = \frac{1}{2 \sqrt{10x-x^2}} \cdot \frac{d}{dx} (10x - x^2)$

$\displaystyle \frac{dR}{dx} = \frac{1}{2 \sqrt{10x-x^2}} (10-2x) = \frac{(10-2x)}{2\sqrt{10x-x^2}} = \frac{2(5-x)}{2 \sqrt{10x-x^2}}$

$\displaystyle \frac{dR}{dx} = \frac{(5-x)}{\sqrt{10x-x^2}}$

Paso 4.. Si $\displaystyle dR/dx$ es nula

$\displaystyle \frac{dR}{dx} = \frac{(5-x)}{\sqrt{10x-x^2}}$

$\displaystyle 0 = \frac{(5-x)}{\sqrt{10x-x^2}}$

$0=5-x$

$\therefore x=5$

Sustituyendo este valor con el despeje de “ $y$ ” de la ecuación suma

$y=10-x$

$y=10-5$

$\therefore y=5$

Paso 5. Calculando la segunda derivada de la función “ $R$ ” en ambos miembros

$\displaystyle \frac{d}{dx} \left(\frac{dR}{dx} \right) = \frac{d}{dx} \left[ \frac{(5-x)}{\sqrt{10x-x^2}} \right]$

$\displaystyle \frac{d^2 R}{dx^2} = \frac{\sqrt{10x - x^2} \cdot \frac{d}{dx} (5-x) - (5-x) \cdot \frac{d}{dx} \left(\sqrt{10x - x^2} \right)}{(\sqrt{10x - x^2})^2}$

$\displaystyle \frac{d^2 R}{dx^2} = \frac{\sqrt{10x-x^2} \cdot (-1) - (5-x) \cdot \left[\frac{1}{2 \sqrt{10x - x^2}} \cdot \frac{d}{dx} (10x-2x^2) \right]}{(\sqrt{10x-x^2})^2}$

$\displaystyle \frac{d^2 R}{dx^2} = \frac{\sqrt{10x-x^2} \cdot (-1) - (5-x) \cdot \left[\frac{1}{2 \sqrt{10x - x^2}} \cdot (10 - 2x) \right]}{(\sqrt{10x-x^2})^2}$

$\displaystyle \frac{d^2 R}{dx^2} = \frac{- \sqrt{10x-x^2} - \left[\frac{(5-x)(10-2x)}{2 \sqrt{10x - x^2}} \right]}{(\sqrt{10x-x^2})^2}$

$\displaystyle \frac{d^2 R}{dx^2} = \frac{- \sqrt{10x-x^2} - \left[\frac{(5-x)\cdot 2(5-x)}{2 \sqrt{10x - x^2}} \right]}{(10x-x^2)}$

$\displaystyle \frac{d^2 R}{dx^2} = \frac{- \sqrt{10x-x^2} - \left[\frac{(5-x)^2}{\sqrt{10x - x^2}} \right]}{(10x-x^2)}$

$\displaystyle \frac{d^2 R}{dx^2} = \frac{- \sqrt{10x-x^2} - \left[\frac{(25 - 10x + x^2)}{\sqrt{10x - x^2}} \right]}{(10x-x^2)}$

$\displaystyle \frac{d^2 R}{dx^2} = \frac{- \frac{\sqrt{10x-x^2} \cdot \sqrt{10x-x^2}}{\sqrt{10x-x^2}} - \left[\frac{(25 - 10x + x^2)}{\sqrt{10x - x^2}} \right]}{(10x-x^2)}$

$\displaystyle \frac{d^2 R}{dx^2} = \frac{-\frac{(10x-x^2)}{\sqrt{10x-x^2}} - \left[\frac{(25 - 10x + x^2)}{\sqrt{10x - x^2}} \right]}{(10x-x^2)}$

$\displaystyle \frac{d^2R}{dx^2} = \frac{\frac{-(10x-x^2) - (25-10x+x^2)}{\sqrt{10x-x^2}}}{(10x-x^2)} = \frac{-10x+x^2-25+10x-x^2}{(10x-x^2)^{3/2}}$

$\displaystyle \frac{d^2 R}{dx^2} = \frac{-25}{(10x-x^2)^{3/2}}$

Si $x=5$

$\displaystyle \frac{d^2 R}{dx^2} = \frac{-25}{[10(5)-(5)^2]^{3/2}}$

$\displaystyle \frac{d^2 R}{dx^2} = \frac{-25}{(50-25)^{3/2}} =\frac{-(25)}{(25)^{3/2}}$

$\displaystyle \frac{d^2R}{dx^2} = \frac{-1}{(25)^{1/2}}$

Como $\displaystyle \frac{d^2 R}{dx^2}<0$ , se dice que los valores de $x$ y $y$ son máximos. Para conocer el valor máximo de la ecuación $R$ , se sustituye con los valores de “x” y de “y” calculados.

$\displaystyle R = \sqrt{xy}$

$\displaystyle R = \sqrt{(5)(5)}$

$\displaystyle R = \sqrt{25}$

$R = 5$

O también,

$\displaystyle R = \sqrt{10x-x^2}$

$\displaystyle R = \sqrt{10(5)-(5)^2} = \sqrt{50-25}$

$\displaystyle R = \sqrt{25}$

$R=5$

Por lo tanto, los dos números son $x=5$ y $y=5$ para que la raíz cuadrada del producto de ambos números (la función $R$ ) sea máxima, cuyo resultado es 5.

La suma de dos números es… . Máximos y mínimos. Aplicaciones de cálculo diferencial.

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta

La suma de dos números es… . Máximos y mínimos. Aplicaciones de cálculo diferencial.

Comparte esto:

Relacionado

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta