El cono circular circunscrito en la esfera. Máximos y mínimos. Aplicaciones de cálculo diferencial.

Problema. Se circunscribe un cono circular recto a una esfera de radio “ $a$ ”. ¿Cuáles deben ser las medidas del cono tales que su volumen sea mínima?

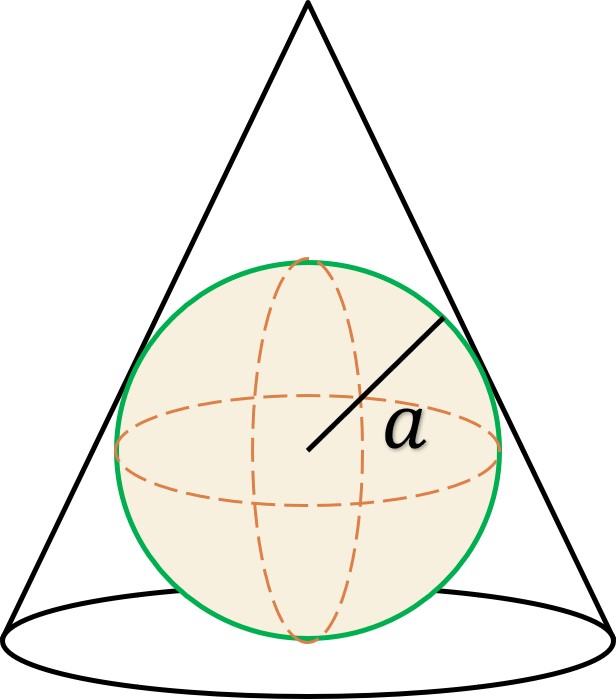
*Figura 4.7.1 Representando el cono circular que está circunscrito en la esféra de radio $a$ .*

Solución. Analizando la figura, se tienen los siguientes datos

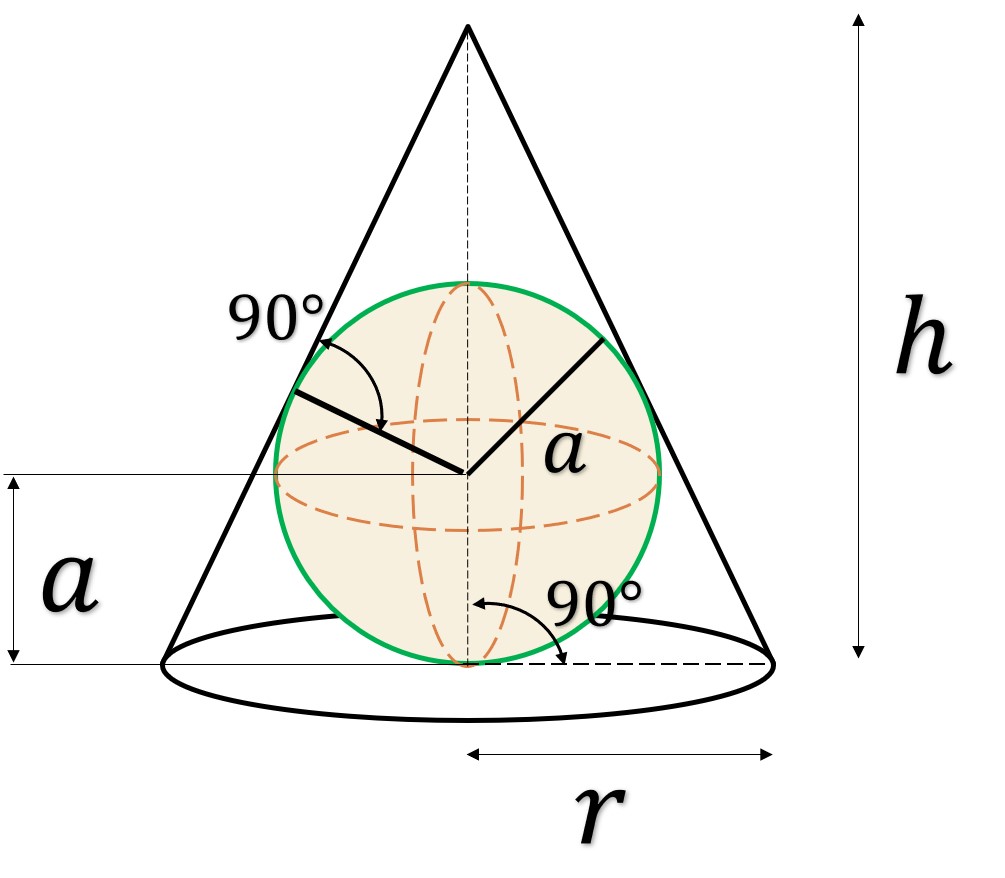
*Figura 4.7.2 Análsis del cono circular circunscrito en la esféra.*

Paso 1. Se sabe que el volumen del cono es

$\displaystyle V = \frac{\pi}{3} r^2 h$

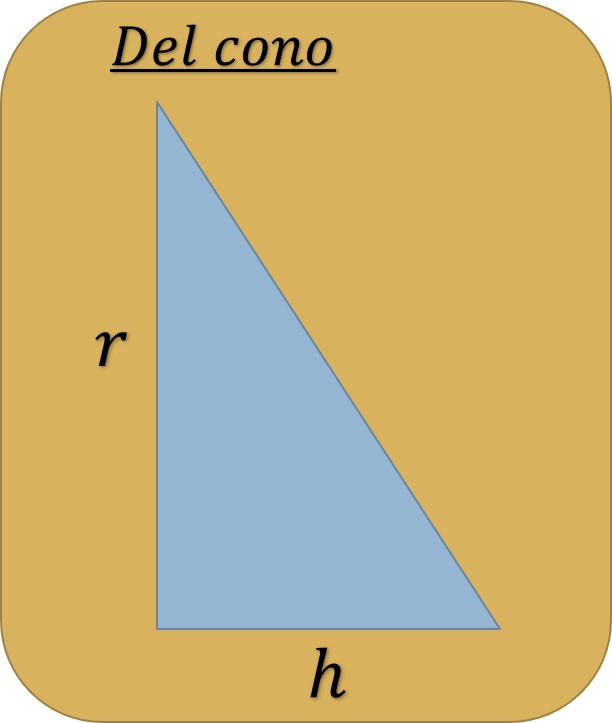
Paso 2. Por semejanza de triángulos, del cono se tiene que

*Figura 4.7.3 Análisis del cono circular.*

Y para la esfera

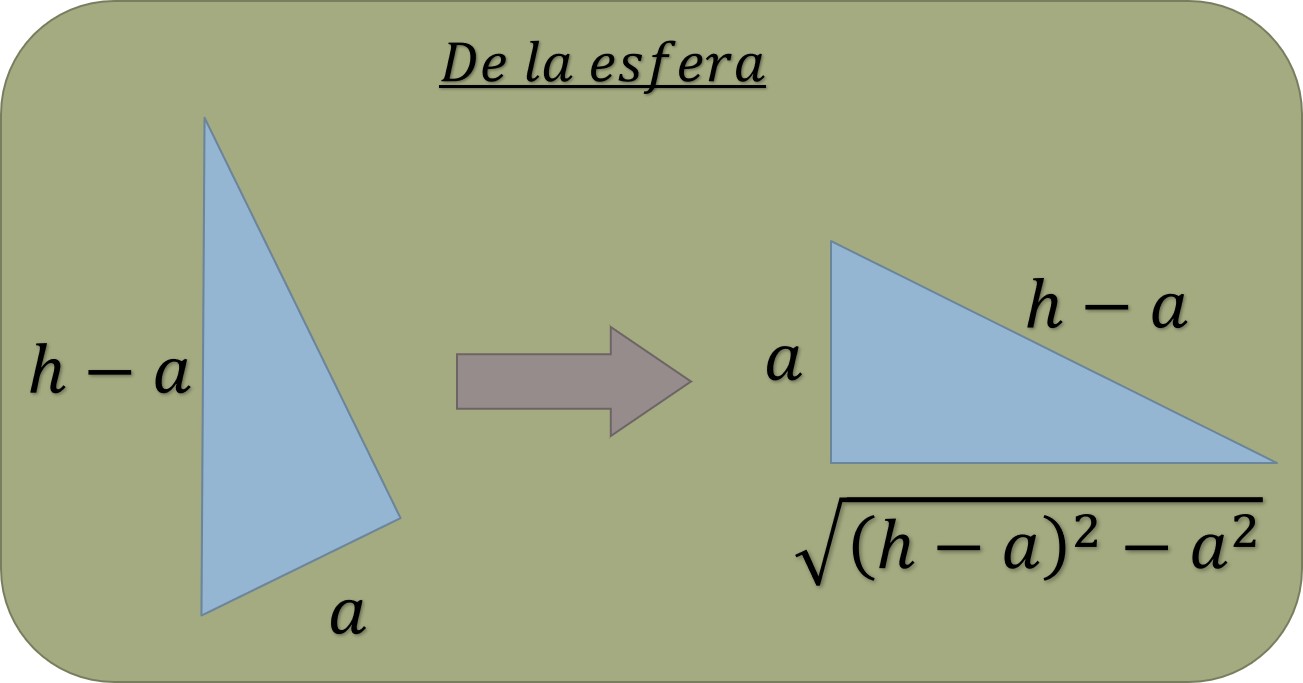
Se sabe que

$\displaystyle \frac{r}{a} = \frac{h}{\sqrt{(h-a)^2-a^2}}$

Y por medio de esto, es necesario contar con $r^2$ . Es decir

$\displaystyle \frac{r}{a} = \frac{h}{\sqrt{(h-a)^2-a^2}}$

$\displaystyle \frac{r}{a} = \sqrt{\frac{h^2}{(h-a)^2-a^2}}$

$\displaystyle \left( \frac{r}{a} \right)^2 = \frac{h^2}{(h-a)^2-a^2}$

$\displaystyle \frac{r^2}{a^2} = \frac{h^2}{(h-a)^2-a^2}$

$\displaystyle r^2 = \frac{a^2 h^2}{(h-a)^2-a^2}$

Paso 3. Sustituyendo esto último en la ecuación del volumen

$\displaystyle V = \frac{\pi}{3} r^2 h$

$\displaystyle V = \frac{\pi}{3} \left[\frac{a^2 h^2}{(h-a)^2-a^2} \right] h$

$\displaystyle V = \frac{\pi}{3} \left[ \frac{a^2 h^3}{(h-a)^2-a^2} \right] = \frac{\pi}{3} \left(\frac{a^2 h^3}{h^2-2ah+a^2-a^2} \right)$

$\displaystyle V = \frac{\pi}{3} \left( \frac{a^2 h^3}{h^2-2ah} \right) = \frac{\pi}{3} \left[ \frac{h(a^2 h^2)}{h(h-2a)} \right]$

$\displaystyle V = \frac{\pi}{3} \left( \frac{a^2 h^2}{h-2a} \right)$

Paso 4. Derivándolo con respecto a la variable independiente (o sea, con respecto a “ $h$ ”)

$\displaystyle \frac{dV}{dh} = \frac{d}{dh} \left[\frac{\pi}{3} \left( \frac{a^2 h^2}{h-2a} \right) \right]$

$\displaystyle \frac{dV}{dh} = \frac{\pi}{3} \frac{d}{dh} \left( \frac{a^2 h^2}{h-2a} \right)$

$\displaystyle \frac{dV}{dh} = \left(\frac{\pi}{3} \right) \left[ \frac{(h-2a) \cdot \frac{d}{dh} (a^2 h^2) - (a^2 h^2) \cdot \frac{d}{dh} (h-2a)}{(h-2a)^2} \right]$

$\displaystyle \frac{dV}{dh} = \left(\frac{\pi}{3} \right) \left[ \frac{(h-2a)(2a^2 h) - (a^2 h^2 )(1)}{(h-2a)^2} \right]$

$\displaystyle \frac{dV}{dh} = \left(\frac{\pi}{3} \right) \left[ \frac{(2a^2 h^2 - 2a^3 h) - (a^2 h^2)}{(h-2a)^2} \right] = \left(\frac{\pi}{3} \right) \left[ \frac{2a^2 h^2 - 2a^3 h - a^2 h^2}{(h-2a)^2} \right]$

$\displaystyle \frac{dV}{dh} = \left(\frac{\pi}{3} \right) \left[ \frac{a^2 h^2 - 2a^3 h}{(h-2a)^2} \right] = \frac{\pi}{3} \left[\frac{a^2 (h^2-4ah)}{(h-2a)^2} \right]$

$\displaystyle \frac{dV}{dh} = \frac{\pi}{3} a^2 \left[ \frac{h^2-4ah}{(h-2a)^2} \right]$

Paso 5. Si $\displaystyle dV/dh$ es nula

$\displaystyle \frac{dV}{dh} = \frac{\pi}{3} a^2 \left[\frac{h^2-4ah}{(h-2a)^2} \right]$

$\displaystyle 0 = \frac{\pi}{3} a^2 \left[\frac{h^2-4ah}{(h-2a)^2} \right]$

Si $a \ne 0$ , se tiene que

$\displaystyle 0 = \frac{\pi}{3} a^2 \left[\frac{h^2-4ah}{(h-2a)^2} \right]$

$\displaystyle 0 \cdot \frac{3}{\pi} \cdot \frac{1}{a^2} = \frac{h^2-4ah}{(h-2a)^2}$

$\displaystyle 0 = \frac{h^2-4ah}{(h-2a)^2}$

Si $(h-2a)^2 \ne 0$ , entonces

$\displaystyle 0 = \frac{h^2-4ah}{(h-2a)^2}$

$0 \cdot (h-a)^2 = h^2 - 4ah$

$0 = h^2 - 4ah$

$h^2 - 4ah = 0$

$h(h-4a) = 0$

Y se obtienen dos soluciones, $h=0$ y $h=4a$ . Por lo que, la segunda solución es la adecuada. Con $h=4a$ , se sustituye en la ecuación $r^2$

$\displaystyle r^2 = \frac{a^2 h^2}{(h-a)^2-a^2}$

$\displaystyle r^2 = \frac{a^2 (4a)^2}{(4a-a)^2-a^2}$

$\displaystyle r^2 = \frac{a^2 (16a^2)}{(3a)^2-a^2}$

$\displaystyle r^2 = \frac{16a^4}{9a^2 - a^2}$

$\displaystyle r^2 = \frac{16a^4}{8a^2}$

$\displaystyle r^2 = 2a^2$

Despejando “ $r$ ”

$r^2=2a^2$

$\displaystyle r = \sqrt{2a^2}$

$\displaystyle \therefore r = \sqrt{2} a$

Paso 6. Derivando la primera función por segunda vez

$\displaystyle \frac{d}{dh} \left(\frac{dV}{dh} \right) = \frac{d}{dh} \left\{\frac{\pi}{3} a^2 \left[\frac{h^2-4ah}{(h-2a)^2} \right] \right\}$

$\displaystyle \frac{d^2 V}{dh^2} = \frac{\pi}{3} a^2 \frac{d}{dh} \left[\frac{h^2-4ah}{(h-2a)^2} \right]$

$\displaystyle \frac{d^2 V}{dh^2} = \frac{\pi}{3} a^2 \left\{\frac{(h-2a)^2 \cdot \frac{d}{dh} (h^2-4ah) - (h^2 - 4ah) \cdot \frac{d}{dh} [(h-2a)^2]}{[(h-2a)^2]^2} \right\}$

$\displaystyle \frac{d^2 V}{dh^2} = \frac{\pi}{3} a^2 \left[\frac{(h-2a)^2 \cdot (2h-4a) - (h^2 - 4ah) \cdot [2(h-2a) \frac{d}{dh} (h-2a)]}{(h-2a)^4} \right]$

$\displaystyle \frac{d^2 V}{dh^2} = \frac{\pi}{3} a^2 \left[\frac{(h-2a)^2 \cdot (2h-4a) - (h^2 - 4ah) \cdot [2(h-2a) (1)]}{(h-2a)^4} \right]$

$\displaystyle \frac{d^2 V}{dh^2} = \frac{\pi}{3} a^2 \left[\frac{(h-2a)^2 (2h-4a) - 2(h-2a)(h^2 - 4ah)}{(h-2a)^4} \right]$

$\displaystyle \frac{d^2 V}{dh^2} = \frac{\pi}{3} a^2 \left\{\frac{(h-2a)[(h-2a) (2h-4a) - 2(h^2 - 4ah)]}{(h-2a)^4} \right\}$

$\displaystyle \frac{d^2 V}{dh^2} = \frac{\pi}{3} a^2 \left[\frac{(h-2a) (2h-4a) - 2(h^2 - 4ah)}{(h-2a)^3} \right]$

$\displaystyle \frac{d^2 V}{dh^2} = \frac{\pi}{3} a^2 \left[\frac{2h^2 - 4ah - 4ah + 8a^2 - 2h^2 + 8ah}{(h-2a)^3} \right]$

$\displaystyle \frac{d^2 V}{dh^2}= \frac{\pi}{3} a^2 \left[\frac{8a^2}{(h-2a)^3} \right]$

$\displaystyle \frac{d^2 V}{dh^2} = \frac{8\pi}{3} a^4 \left[\frac{1}{(h-2a)^3} \right]$

Si $h=4a$

$\displaystyle \frac{d^2 V}{dh^2} = \frac{8\pi}{3} a^4 \left[\frac{1}{(4a-2a)^3} \right]$

$\displaystyle \frac{d^2 V}{dh^2} = \frac{8\pi}{3} a^4 \left[\frac{1}{(2a)^3} \right]$

$\displaystyle \frac{d^2 V}{dh^2} = \frac{8\pi}{3} a^4 \left(\frac{1}{8a^3} \right)$

$\displaystyle \frac{d^2 V}{dh^2} = \frac{\pi}{3} a$

Como $\displaystyle \frac{d^2 V}{dh^2}>0$ , se trata de un mínimo. Por lo tanto, si $h=4a$ y $\displaystyle r = \sqrt{2}$ a, el volumen del cono circunscrito será mínimo.

El cono circular circunscrito en la esfera. Máximos y mínimos. Aplicaciones de cálculo diferencial.

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta

El cono circular circunscrito en la esfera. Máximos y mínimos. Aplicaciones de cálculo diferencial.

Comparte esto:

Relacionado

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta