Un rectángulo inscrito en un triángulo. Máximos y mínimos. Aplicaciones de cálculo diferencial.

Problema. Hay un triángulo escaleno de base 12 (cm) con una altura de 6(cm). Hallar el área del mayor rectángulo inscrito cuya base coincida con la base del triángulo.

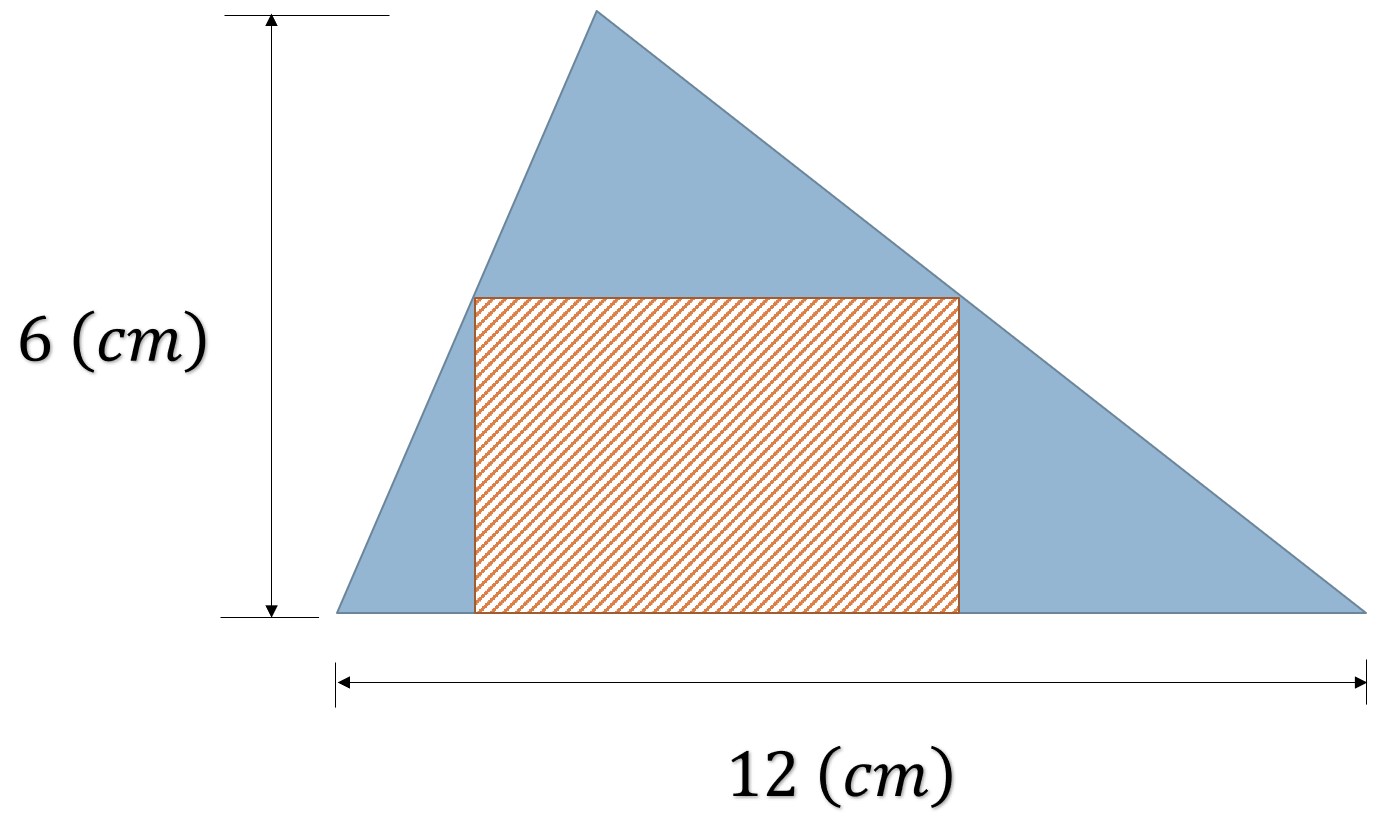
*Figura 4.10.1 Triángulo circunscrito en el rectángulo.*

Solución. Analizando más a detalle el rectángulo inscrito en el triángulo escaleno

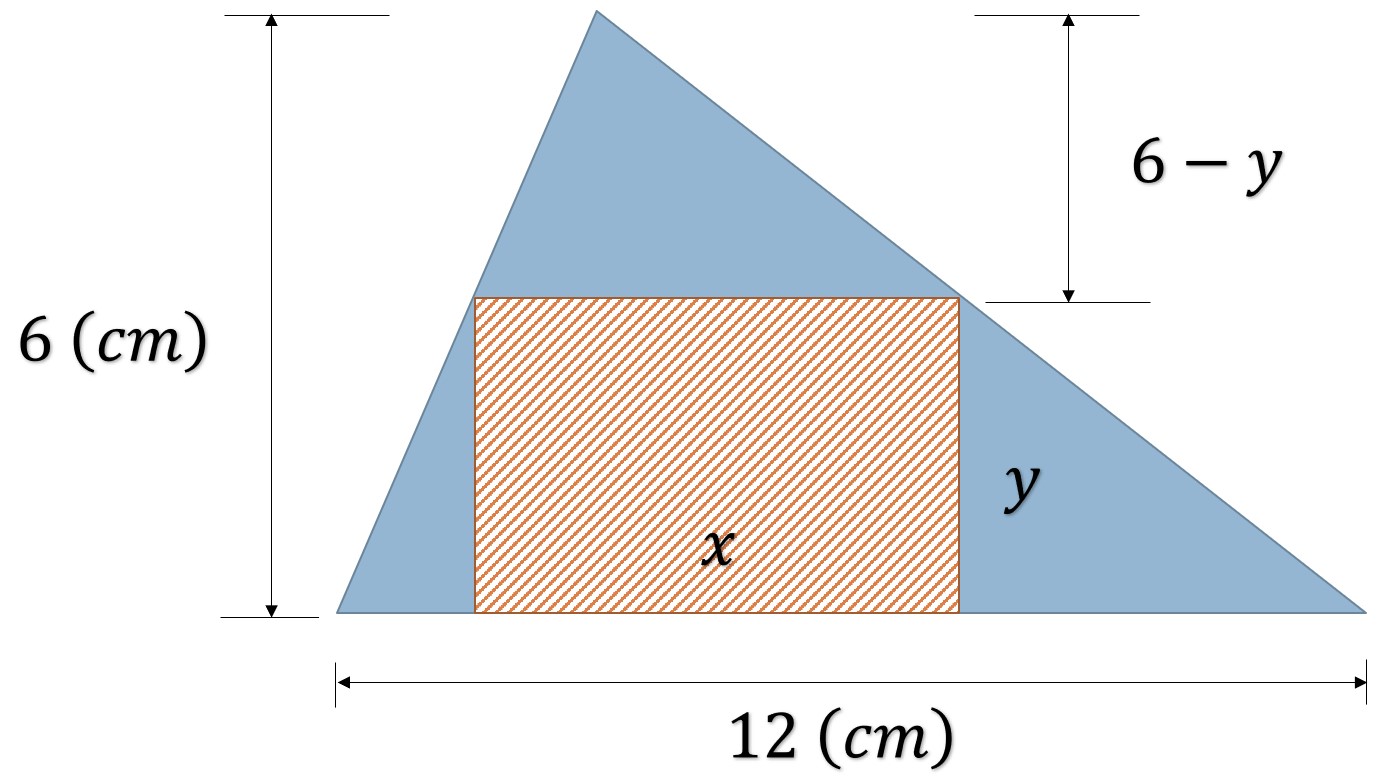
*Figura 4.10.2 Analisis del rectángulo inscrito en el triángulo.*

Paso 1. Por semejanza de triángulos

$\displaystyle \frac{6}{6-y} = \frac{12}{x}$

Figura 4.10.3
Figura 4.10.4

Despejando “ $y$ ”

$\displaystyle \frac{6}{6-y} = \frac{12}{x}$

$\displaystyle 6x = 12(6-y)$

$6x=72-12y$

$12y=72-6x$

$\displaystyle y = 6 - \frac{1}{2} x$

Paso 2. El área del rectángulo es

$A=xy$

Donde está dado en ( $cm^2$ ).

Paso 3. Sustituyendo la ecuación “y” en la ecuación del área.

$\displaystyle A = xy = x(6 - \frac{1}{2} x)$

$\displaystyle A = 6x - \frac{1}{2} x^2$

Paso 4. Derivando el área con respecto a “ $x$ ”

$\displaystyle \frac{d}{dx} (A) = \frac{d}{dx} \left(6x - \frac{1}{2} x^2 \right)$

$\displaystyle \frac{dA}{dx} = 6 - x$

Paso 5. Si $\displaystyle \frac{dA}{dx} = 0$

$0 = 6 - x$

$x = 6$

Tomando este último valor y sustituyendo en la ecuación de “ $y$ ”

$\displaystyle y = 6 - \frac{1}{2} x$

$y = 6 - \frac{1}{2} (6)$

$y=3$

Si $x=6$ y $y=3$ , el área del rectángulo es

$A=xy$

$A=(6)(3)$

$A=18$

Donde el área está dado en ( $cm^2$ ).

Paso 6. Derivando nuevamente el área con respecto a “ $x$ ”

$\displaystyle \frac{d}{dx} \left( \frac{dA}{dx} \right) = \frac{d}{dx} (6 - x)$

$\displaystyle \frac{d^2 A}{dx^2} = - 1$

Con $\displaystyle \frac{d^2 A}{dx^2} < 0$ se trata de un máximo. Por lo tanto, el rectángulo inscrito tendrá un área máxima de 18 $cm^2$ , donde su base será de 6 (cm) y su altura de 3 (cm), es decir, la altura tendrá la mitad de su base.

Publicado por Cesar Reyes

Dedicado a compartir información temas referentes al cálculo básicos, intermedios y avanzados mediante presentaciones PDF, videos y publicaciones en este sitio web. Ver todas las entradas de Cesar Reyes

Deja un comentario Cancelar la respuesta

Este sitio utiliza Akismet para reducir el spam. Conoce cómo se procesan los datos de tus comentarios.

Un rectángulo inscrito en un triángulo. Máximos y mínimos. Aplicaciones de cálculo diferencial.

Comparte esto:

Relacionado

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta