22 julio, 201916 junio, 2019 Cesar Reyes aplicaciones de cálculo diferencial, blog

El rectángulo y las rectas. Máximos y mínimos. Aplicaciones de cálculo diferencial.

Problema. Hay un rectángulo que tiene dos de sus vértices sobre el eje OX y los otros dos vértices sobre las rectas: y=18-3x, y=x. Hallar el área máxima que puede tener el rectángulo.

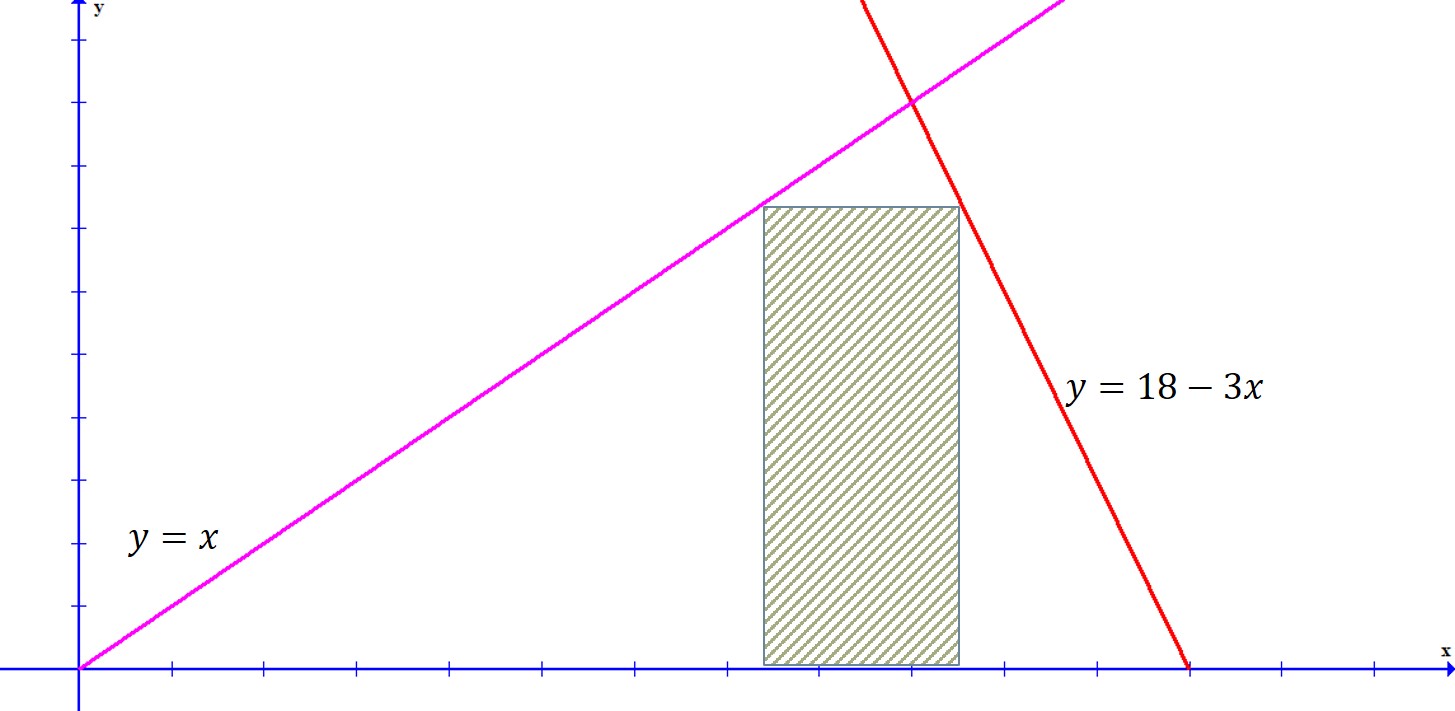
Figura 4.15.1 Representación gráfica del problema.

Solución. Se localizan los puntos que forman el vértice del rectángulo.

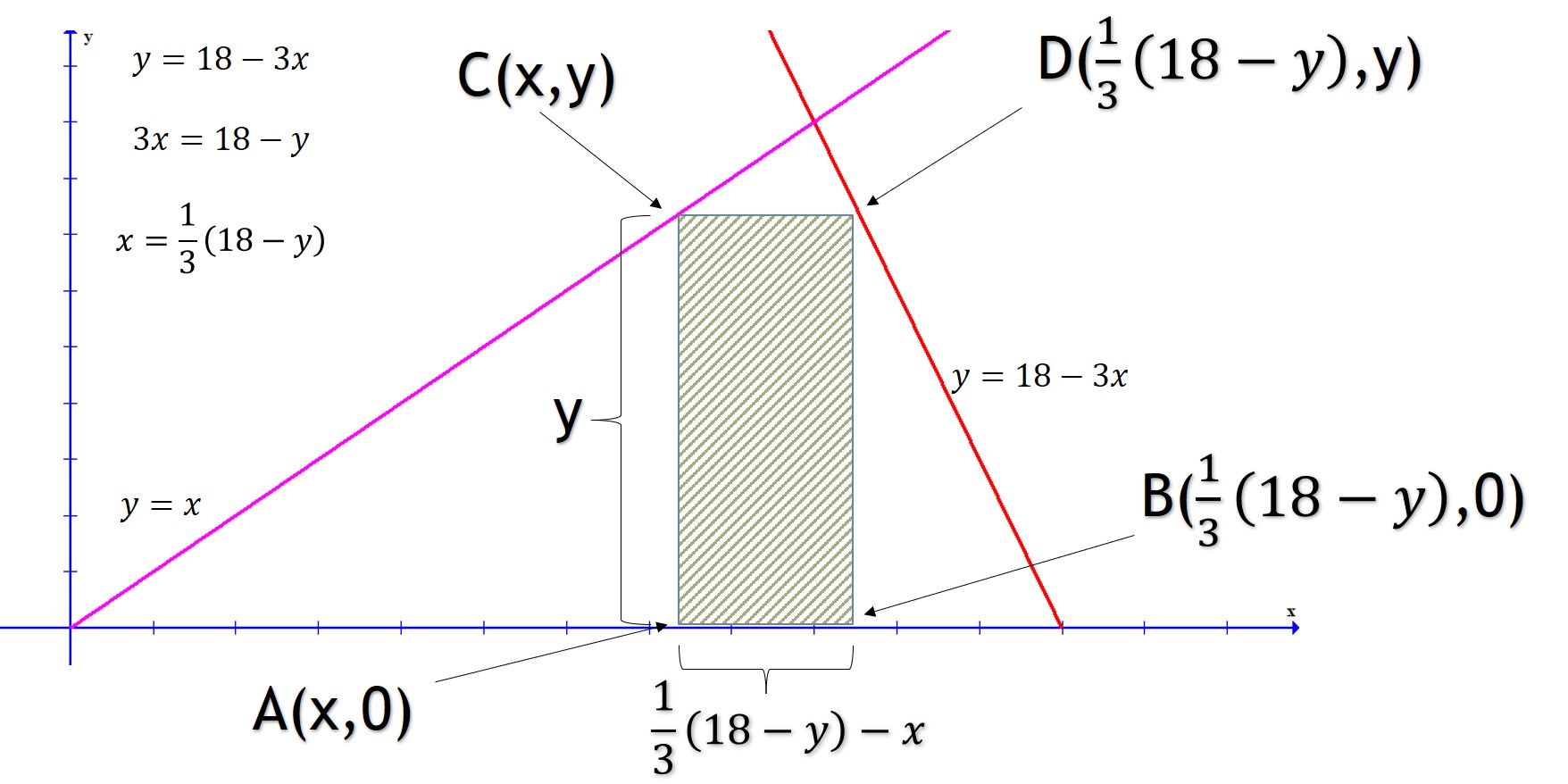
Figura 4.15.2 Localizando los vértices del rectángulo.

Paso 1. El área del rectángulo es

$A = \text{base} \cdot \text{altura}$

$A = \overline{AB} \cdot \overline{AC}$

$\displaystyle A = \left[ \frac{1}{3} (18 - y) - x \right] \cdot y$

Paso 2. La coordenada “ $x$ ” corresponde a “ $y$ ” por estar bajo la recta.

$y = x$

Paso 3. Sustituyendo esta ecuación en la expresión de “ $A$ ”

$\displaystyle A = \left[ \frac{1}{3} (18 - y) - x \right] \cdot y$

$\displaystyle A = \left[ \frac{1}{3} (18 - x) - x \right] \cdot x$

$\displaystyle A = \left(6 - \frac{1}{3} x - x \right) \cdot x$

$\displaystyle A = \left( 6 - \frac{4}{3} x \right) x$

$\displaystyle A = \left(6x - \frac{4}{3} x^2 \right)$

Paso 4. Derivando la nueva expresión de $A$ con respecto a “ $x$ ”

$\displaystyle \frac{d}{dx} (A) = \frac{d}{dx} \left(6x - \frac{4}{3} x^2 \right)$

$\displaystyle \frac{dA}{dx} = 6 \frac{d}{dx} (x) - \frac{4}{3} \frac{d}{dx} (x^2)$

$\displaystyle \frac{dA}{dx} = 6 - \frac{8}{3} x$

Paso 5. Si $\displaystyle \frac{dA}{dx} = 0$

$\displaystyle \frac{dA}{dx} = 6 - \frac{8}{3} x$

$\displaystyle 0 = 6 - \frac{8}{3} x$

$\displaystyle \frac{8}{3} x = 6$

$\displaystyle x = \frac{18}{8} = \frac{9}{4}$

De la ecuación $y=x$ , el valor de “ $y$ ” será

$\displaystyle y = \frac{9}{4}$

Paso 6. De los cuatro vértices del rectángulo, los puntos son

$\displaystyle A(x,0) = A \left(\frac{9}{4}, 0 \right)$

$\displaystyle B \left[\frac{1}{3} (18 - y),0 \right] = B \left(\frac{21}{4},0 \right)$

$\displaystyle C(x,y) = C \left( \frac{9}{4}, \frac{9}{4} \right)$

$\displaystyle D \left[\frac{1}{3} (18 - y), y \right] = D \left(\frac{21}{4}, \frac{9}{4} \right)$

Calculando el área del rectángulo [tomando el punto $C(x,y)$ ]

$\displaystyle A = \left[\frac{1}{3} (18 - y) - x \right] \cdot y$

$\displaystyle A = \left[\frac{1}{3} \left(18 - \frac{9}{4} \right) - \frac{9}{4} \right] \cdot \frac{9}{4}$

$\displaystyle A = (3) \cdot \left( \frac{9}{4} \right)$

$\displaystyle A = \frac{27}{4} \ (u^2)$

Donde la base es de 3 unidades y la altura de 9/4 unidades.

Determinando el punto de corte entre las dos rectas

$\displaystyle y = 18 - 3x$

$x = 18 - 3x$

$4x = 18$

$\displaystyle x = \frac{18}{4} = \frac{9}{2}$

El punto de corte entre ambas rectas es $\displaystyle \left(\frac{9}{2}, \frac{9}{2} \right)$ .

Derivando nuevamente el resultado de la primera derivada de $A$

$\displaystyle \frac{d}{dx} \left(\frac{dA}{dx} \right) = \frac{d}{dx} \left(6 - \frac{8}{3} x \right)$

$\displaystyle \frac{d^2 A}{dx^2} = -\frac{8}{3}$

Como $\displaystyle \frac{d^2 A}{dx^2} < 0$ se trata de un mínimo.

Por lo tanto, con una base de 3 unidades y una altura de $\displaystyle \frac{9}{4}$ , se tendrá un área máxima de $\displaystyle \frac{27}{4} = 6.75$ unidades cuadradas.

Publicado por Cesar Reyes

Dedicado a compartir información temas referentes al cálculo básicos, intermedios y avanzados mediante presentaciones PDF, videos y publicaciones en este sitio web. Ver todas las entradas de Cesar Reyes

Deja un comentario Cancelar la respuesta

Este sitio utiliza Akismet para reducir el spam. Conoce cómo se procesan los datos de tus comentarios.