Funciones especiales. Laplace.

Función gamma

Si $n>0$ , la función gamma se define por

$\displaystyle \Gamma (n) = \int_{0}^{\infty}{u^{n-1} e^{-u} \ du}$

Las propiedades de la función gamma son:

1.- Se tiene

$\displaystyle \Gamma (n+1) = n \Gamma (n)$ , $n >0$

Como $\Gamma (1) = 1$ , entonces $\Gamma (2)=1$ , $\Gamma (3) = 2!$ , $\Gamma (4) = 3!$ y en general $\Gamma (n+1) = n!$ , si $n$ es un entero positivo. Por esta razón la función gamma se llama a veces función factorial.

2.- Cuando $\displaystyle n =\frac{1}{2}$

$\displaystyle \Gamma \left(\frac{1}{2} \right) = \sqrt{\pi}$

3.- Para un producto de dos funciones gamma

$\displaystyle \Gamma (p) \Gamma (p-1) = \frac{\pi}{\sin{p\pi}}$ , $0<p<1$

4.- Cuando $n$ sea convenientemente grande,

$\displaystyle \Gamma (n+1) \approx \sqrt{2 \pi n} \cdot n^n e^{-n}$

5.- Si $n<0$ , se puede definir $\Gamma (n)$ por

$\displaystyle \Gamma (n) = \frac{\Gamma (n+1)}{n}$

Función de Bessel

Se define una función Bessel de orden $n$ por medio de

$\displaystyle J_n (t) = \frac{t^n}{2^n \Gamma (n+1)} \left[ 1 - \frac{t^2}{2(2n+2)} + \frac{t^4}{2 \cdot 4 (2n+2)(2n+4)} - \cdots \right]$

Algunas propiedades importantes son

1.- $J_{-n} (t) = (-1)^n J_n (t)$ si $n$ es un entero positivo.

2.- $\displaystyle J_{n+1} (t) = \frac{2n}{t} J_n (t) - J_{n-1} (t)$ .

3.- $\displaystyle \frac{d}{dt} [t^n J_n (t)] = t^n J_{n-1} (t)$ . Si $n=0$ , se tiene $J_0'(t) = - J_1 (t)$ .

4.- $\displaystyle e^{\frac{1}{2} t(u - \frac{1}{u})} = \sum_{n=-\infty}^{\infty}{J_n(t) u^n}$ . Esta se llama la función generadora para las funciones de Bessel.

5.- $J(t)$ satisface la ecuación diferencial de Bessel, es decir,

$\displaystyle t^2 y''(t) + ty'(t) + (t^2-n^2) y(t) = 0$

Es conveniente definir $J_n(it) = i^{-n} i(t)$ ; $i(t)$ se llama la función modificada de Bessel de orden $n$ .

Función de error

Esta función se define como

$\displaystyle \text{fer} (t) = \frac{2}{\sqrt{\pi}} \int_{0}^{t}{e^{-u^2} \ du}$

Función complementaria de error

Se define como

$\displaystyle \text{fce}(t) = 1 - \text{fer}(t)$

$\displaystyle \text{fce}(t) = 1 - \frac{2}{\sqrt{\pi}} \int_0^t{e^{-u^2} \ du}$

$\displaystyle \text{fce}(t) = \frac{2}{\sqrt{\pi}} \int_{t}^{\infty}{e^{-u^2} \ du}$

Integral de la función seno

Se define como

$\displaystyle \text{Is} (t) = \int_0^t{\frac{\sin{\tau}}{\tau} \ d\tau}$

Integral de la función coseno

Se define como

$\displaystyle \text{Ic} (t) = \int_t^{\infty}{\frac{\cos{\tau}}{\tau} \ d\tau}$

Integral de la función exponencial

Se define como

$\displaystyle \text{Ie} (t) = \int_t^{\infty}{\frac{e^{-\tau}}{\tau} \ d\tau}$

Función escalonada unitaria

También conocida como función unitaria de Heaviside, se define como

$\displaystyle U (t-a) = \left\{ \begin{matrix} 0 \quad \text{para} \ t < a \\ 1 \quad \text{para} \ t>a \end{matrix} \right.$

Funcion unitaria de Heaviside — *Figura 1. Representación gráfica de una función escalonada unitaria (R. Spiegel, 1996).*

Función de impulso unitario

También llamado función delta de Dirac y se considera la función

$\displaystyle f_{\epsilon} (t) = \left\{ \begin{matrix} \frac{1}{\epsilon} \quad \text{para} \ 0 \le t \le \epsilon \\ 0 \quad \quad \quad \text{para} \ t>\epsilon \end{matrix} \right.$

donde $\epsilon > 0$ ; su gráfica es la siguiente:

FunciÃ³n delta de Dirac.png — *Figura 1. Representación gráfica de una función escalonada unitaria (R. Spiegel, 1996).*

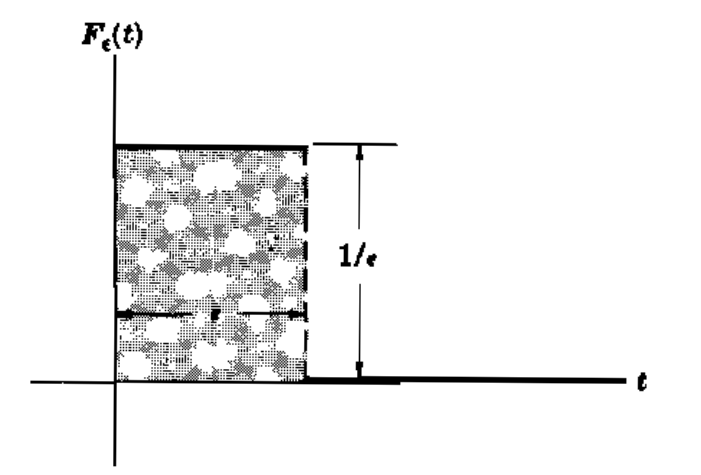
Geométricamente es evidente que cuando $\epsilon \rightarrow 0$ , la altura de la región rectangular sombreada crece indefinidamente y la base decrece, en tal forma que el área es siempre igual a 1, es decir

$\displaystyle \int_0^{\infty}{f_{\epsilon} (t) \ dt} = 1$

Esta idea ha llevado a algunos ingenieros y físicos a pensar en una función limitante, denotada por $\delta (t)$ , aproximada por $f_{\epsilon} (t)$ cuando $\epsilon \rightarrow 0$ . Esta función limitante ha sido llamada la función de impulso unitario o función delta de Dirac. Sus propiedades son:

1.- $\displaystyle \int_{0}^{\infty}{\delta (t)} = 1$ .

2.- $\displaystyle \int_{0}^{\infty}{\delta (t) \ g(t)} = g(0)$ para cualquier función continua $g(t)$ .

3.- $\displaystyle \int_{0}^{\infty}{\delta (t-a) \ g(t)} = g(a)$ para cualquier función continua $g(t)$ .

A pesar de que, matemáticamente hablando, tal función no existe, pueden formalizarse algunas manipulaciones y operaciones con ella.

Funciones nulas

Si $\mathcal{N} (t)$ es una función de $t$ , tal que para todo $t>0$

$\displaystyle \int_{0}^{t}{\mathcal{N} (\tau) \ d\tau} = 0$

donde $latex \mathcal{N} (t) se llamará una función nula.

En general, cualquier función que valga cero en todas partes, excepto, a lo más, en un conjunto enumerable de puntos (es decir, un conjunto de puntos que pueda ponerse en correspondencia biunívoca con los números naturales 1, 2, 3, …) es una función nula.

Funciones especiales. Laplace.

Función gamma

Función de Bessel

Función de error

Función complementaria de error

Integral de la función seno

Integral de la función coseno

Integral de la función exponencial

Función escalonada unitaria

Función de impulso unitario

Funciones nulas

Transformada de Laplace de algunas funciones especiales

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta

Funciones especiales. Laplace.

Función gamma

Función de Bessel

Función de error

Función complementaria de error

Integral de la función seno

Integral de la función coseno

Integral de la función exponencial

Función escalonada unitaria

Función de impulso unitario

Funciones nulas

Transformada de Laplace de algunas funciones especiales

Comparte esto:

Relacionado

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta