Conducción del calor en una dimensión. Problemas de valor frontera. Laplace.

Introducción

Teniendo la siguiente ecuación,

$\displaystyle \frac{\partial u}{\partial t} = k \frac{\partial^2 u}{\partial x^2}$

$u(x,t)$ es la temperatura de un sólido en el punto $x$ en un tiempo $t$ . La constante $k$ , llamada difusión, es igual a $K/c {\rho}$ donde la conductividad térmica $K$ , el calor específico $c$ y la densidad (masa por unidad de volumen) $\rho$ se suponen constantes. La cantidad de calor por unidad de área conducida a través de un plano en la unidad de tiempo está dada por $-K u_x (x,t)$ .

Problemas resueltos

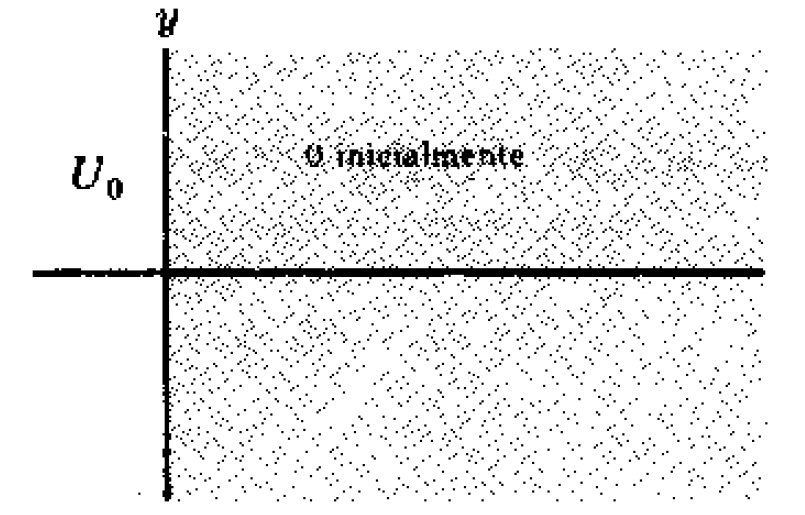
Problema 1. Un sólido semi-infinito $x>0$ (figura 1) está inicialmente a la temperatura cero. En el tiempo $t=0$ se le aplica y se le mantiene una temperatura constante $U_0 >0$ en la cara $late x=0$.

(a) Hallar la temperatura de cualquier punto sólido en cualquier tiempo posterior $t>0$ .
(b) Desarrollar este problema si en $t=0$ la temperatura que se aplica está dada por $g(t)$ , $t>0$ .

*Figura 1. Representación del sólido semi-infinito.*

Solución (a). El problema de valor frontera para la determinación de la temperatura $u(x,t)$ en cualquier punto $x$ y en cualquier tiempo $t$ es

$\displaystyle \frac{\partial u}{\partial t} = k \frac{\partial^2 u}{{\partial x}^2}$ para $x>0$ , $t>0$

Además

$u(x,0)=0$ , $u(0,t)=U_0$ , $|u(x,t)| < M$

donde la última condición indica que la temperatura es constante para todo $x$ y todo $t$ , tal como lo exige el problema.

Tomando la transformada de Laplace en ambos lados y acomodando los términos, se tiene lo siguiente

$\displaystyle \frac{\partial u}{\partial t} = k \frac{\partial^2 u}{{\partial x}^2}$

$\displaystyle \mathcal{L} \left[\frac{\partial u}{\partial t} \right] = k \mathcal{L} \left[ \frac{\partial^2 u}{{\partial x}^2} \right]$

$\displaystyle sU(x,s) - u(x,0) = k \frac{d^2 U}{{dx}^2}$

$\displaystyle sU(x,s) - 0 = k \frac{d^2 U}{{dx}^2}$

$\displaystyle sU(x,s) = k \frac{d^2 U}{{dx}^2}$

$\displaystyle k \frac{d^2 U}{{dx}^2} - s U(x,s) = 0$

$\displaystyle \frac{d^2 U}{{dx}^2} - \frac{s}{k} U(x,s) = 0$

Resolviendo esta ecuación diferencial, resulta que

$\displaystyle U(x,s) = C_1 e^{\sqrt{s/k} x} + C_2 e^{-\sqrt{s/k} x}$

Para determinar las constantes de integración, se escoge $C_1=0$ para que $U$ resulte acotado cuando $x \rightarrow \infty$ . Entonces

$\displaystyle U(x,s) = C_1 e^{\sqrt{s/k} x} + C_2 e^{-\sqrt{s/k} x}$

$\displaystyle U(x,s) = (0) e^{\sqrt{s/k} x} + C_2 e^{-\sqrt{s/k} x}$

$\displaystyle U(x,s) = C_2 e^{-\sqrt{s/k} x}$

Luego, cuando $x=0$ , $\displaystyle U(0,s) = \mathcal{L} [u(0,t)] = \mathcal{L} \left[ U_0 \right] = \frac{U_0}{s}$

$\displaystyle U(x,s) = C_2 e^{-\sqrt{s/k} x}$

$\displaystyle U(0,s) = C_2 e^{-\sqrt{s/k} (0)}$

$\displaystyle \frac{U_0}{s} = C_2 e^0 = C_2 (1)$

$\displaystyle \frac{U_0}{s} = C_2$

Sustituyendo

$\displaystyle U(x,s) = C_2 e^{-\sqrt{s/k} x}$

$\displaystyle U(x,s) = \frac{U_0}{s} e^{-\sqrt{s/k} x}$

Aplicando la transformada inversa de Laplace en ambos miembros

$\displaystyle \mathcal{L}^{-1} [U(x,s)] = \mathcal{L}^{-1} \left[\frac{U_0}{s} e^{-\sqrt{s/k} x} \right]$

$\displaystyle \mathcal{L}^{-1} [U(x,s)] = U_0 \ \mathcal{L}^{-1} \left[\frac{e^{-\sqrt{s/k} x}}{s} \right]$

donde $s=0$ es un punto de ramificación. Continuando

$\displaystyle u(x,t) = U_0 \left(1 - \frac{1}{\pi} \int_0^{\infty}{\frac{e^{-xt} \sin{x \sqrt{\frac{x}{k}}} }{x} \ dx} \right)$

$\displaystyle u(x,t) = U_0 \left(1 - \frac{2}{\pi} \int_0^{x/2\sqrt{k t}}{e^{-u^2} \ du} \right)$

$\displaystyle u(x,t) = U_0 \left[1 - \text{fer} \left(\frac{x}{2 \sqrt{kt}} \right) \right]$

$\displaystyle u(x,t) = U_0 \ \text{fcer} \left(\frac{x}{2 \sqrt{kt}} \right)$

Finalmente

$\displaystyle \therefore u(x,t) = U_0 \left[1 - \text{fer} \left(\frac{x}{2 \sqrt{kt}} \right) \right] = U_0 \ \text{fcer} \left(\frac{x}{2 \sqrt{kt}} \right)$

Solución (b). El problema de valor frontera es en este caso el mismo que el anterior salvo por el hecho de que la condición de frontera $u(0,t)=U_0$ se remplaza por $u(0,t)=g(t)$ . Entonces,

$\displaystyle \frac{\partial u}{\partial t} = k \frac{\partial^2 u}{{\partial x}^2}$

$\displaystyle \mathcal{L} \left[\frac{\partial u}{\partial t} \right] = k \mathcal{L} \left[ \frac{\partial^2 u}{{\partial x}^2} \right]$

$\displaystyle sU(x,s) - u(x,0) = k \frac{d^2 U}{{dx}^2}$

$\displaystyle sU(x,s) - 0 = k \frac{d^2 U}{{dx}^2}$

$\displaystyle sU(x,s) = k \frac{d^2 U}{{dx}^2}$

$\displaystyle k \frac{d^2 U}{{dx}^2} - s U(x,s)=0$

$\displaystyle \frac{d^2 U}{{dx}^2} - \frac{s}{k} U(x,s) = 0$

Resolviendo esta ecuación diferencial, resulta que

$\displaystyle U(x,s) = C_1 e^{\sqrt{s/k} x} + C_2 e^{-\sqrt{s/k} x}$

Para determinar las constantes de integración, se escoge $C_1=0$ para que $U$ resulte acotado cuando $x \rightarrow \infty$ . Entonces

$\displaystyle U(x,s) = (0) e^{\sqrt{s/k} x} + C_2 e^{-\sqrt{s/k} x}$

$\displaystyle U(x,s) = C_2 e^{-\sqrt{s/k} x}$

Luego, cuando $x=0$ , $\displaystyle U(0,s) = \mathcal{L} [u(0,t)] = \mathcal{L} \left[ g(t) \right] = G(s)$

$\displaystyle U(x,s) = C_2 e^{-\sqrt{s/k} x}$

$\displaystyle U(0,s) = C_2 e^{-\sqrt{s/k} (0)}$

$\displaystyle G(s) = C_2 e^{0} = C_2 (1)$

$\displaystyle G(s) = C_2$

Así que,

$\displaystyle U(x,s) = G(s) \ e^{-\sqrt{s/k} x}$

Aplicando la transformada inversa de Laplace en ambos lados

$\displaystyle \mathcal{L}^{-1} [U(x,s)] = \mathcal{L}^{-1} [G(s) \ e^{-\sqrt{s/k} x}]$

Al aplicar el teorema de convolución, se tiene que $\mathcal{L}^{-1} [G(s)] = g(t)$ y $\displaystyle \mathcal{L}^{-1} [e^{-\sqrt{s/k} x} ] = \frac{x}{2\sqrt{\pi k}} t^{-3/2} e^{-x^2/4kt}$ . Por lo que

$\displaystyle u(x,t) = \int_0^t{\frac{x}{2 \sqrt{\pi k}} u^{-3/2} e^{-x^2/4ku} \ g(t-u) \ du}$

Haciendo $\displaystyle v=\frac{x^2}{4ku}$ ,

$\displaystyle u(x,t) = \frac{2}{\sqrt{\pi}} \int_{x/2\sqrt{kt}}^{\infty}{e^{-v^2} \ g \left(t-\frac{x^2}{4kv^2} \right) \ dv}$

Finalmente,

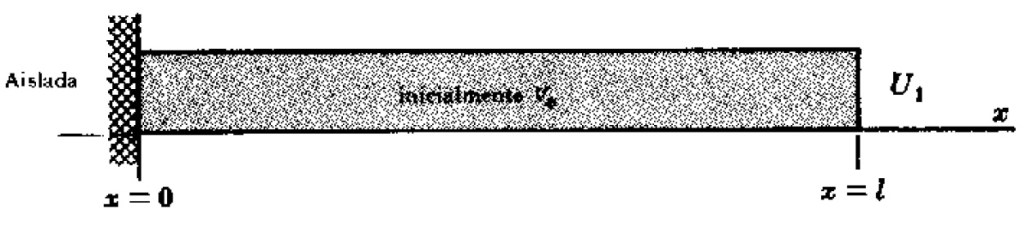
$\displaystyle \therefore u(x,t) = \frac{2}{\sqrt{\pi}} \int_{x/2\sqrt{kt}}^{\infty}{e^{-v^2} \ g \left(t-\frac{x^2}{4kv^2} \right) \ dv}$

Problema 2. Una barra de longitud $l$ (figura 2) está a temperatura constante $U_0$ . Cuando $t>0$ , al extremo $x=l$ se le aplica súbitamente una temperatura constate $U$ , y al extremo $x=0$ se le aisla. Suponiendo que la superficie de la barra está aislada, hallar la temperatura de cualquier punto $x$ de la barra en cualquier tiempo $t>0$ .

*Figura 2. Una barra de longitud «l» que está a temperatura constate U_0.*

Solución. El problema de valor frontera es

$\displaystyle \frac{\partial u}{\partial t} = k \frac{\partial^2 u}{{\partial x}^2}$ para $0<x<l$ , $t>0$

Además

$u(x,0)=U_0$ , $u_x (0,t)=0$ , $u(l,t) = U_1$

Aplicando la transformada de Laplace en ambos lados,

$\displaystyle \mathcal{L} \left[\frac{\partial u}{\partial t} \right] = k \mathcal{L} \left[\frac{\partial^2 u}{{\partial x}^2} \right]$

$\displaystyle sU(x,s) - u(x,0) = k \frac{d^2 U}{{dx}^2}$

También,

$\mathcal{L} [u_x (0,t)] = U_x (0,s) = 0$ , $\displaystyle \mathcal{L} [u(l,t)] = U(l,s) = \frac{U_1}{s}$

Entonces

$\displaystyle sU(x,s) - u(x,0) = k \frac{d^2 U}{{dx}^2}$

$\displaystyle sU(x,s) - U_0 = k \frac{d^2 U}{{dx}^2}$

$\displaystyle k \frac{d^2 U}{{dx}^2} - s U(x,s) = - U_0$

$\displaystyle \frac{d^2 U}{{dx}^2} - \frac{s}{k} U(x,s) = - \frac{U_0}{k}$

La solución general para esta ecuación diferencial es,

$\displaystyle U(x,s) = C_1 \cosh{\sqrt{\frac{s}{k}} x} + C_2 \sinh{\sqrt{\frac{s}{k}} x} + \frac{U_0}{s}$

Derivando con respecto a $x$

$\displaystyle \frac{\partial}{\partial x}[U(x,s)] = C_1 \frac{\partial}{\partial x} \left(\cosh{\sqrt{\frac{s}{k}} x} \right) + C_2 \frac{\partial}{\partial x} \left(\sinh{\sqrt{\frac{s}{k}} x}\right) + \frac{\partial}{\partial x} \left(\frac{U_0}{s} \right)$

$\displaystyle U_x (x,s) = C_1 \sqrt{\frac{s}{k}} \sinh{\sqrt{\frac{s}{k}} x} + C_2 \sqrt{\frac{s}{k}} \cosh{\sqrt{\frac{s}{k}} x} + (0)$

$\displaystyle U_x (x,s) = C_1 \sqrt{\frac{s}{k}} \sinh{\sqrt{\frac{s}{k}} x} + C_2 \sqrt{\frac{s}{k}} \cosh{\sqrt{\frac{s}{k}} x}$

Si $U_x (0,s)=0$ .

$\displaystyle U_x (0,s) = C_1 \sqrt{\frac{s}{k}} \sinh{\sqrt{\frac{s}{k}} (0)} + C_2 \sqrt{\frac{s}{k}} \cosh{\sqrt{\frac{s}{k}} (0)}$

$\displaystyle 0 = C_1 \sqrt{\frac{s}{k}} \sinh{(0)} + C_2 \sqrt{\frac{s}{k}} \cosh{(0)}$

$\displaystyle 0 = C_1 \sqrt{\frac{s}{k}} (0) + C_2 \sqrt{\frac{s}{k}} (1)$

$\displaystyle 0 = C_2 \sqrt{\frac{s}{k}}$

$\displaystyle C_2 = 0$

Sustituyendo

$\displaystyle U(x,s) = C_1 \cosh{\sqrt{\frac{s}{k}} x} + (0) \sinh{\sqrt{\frac{s}{k}} x} + \frac{U_0}{s}$

$\displaystyle U(x,s) = C_1 \cosh{\sqrt{\frac{s}{k}} x} + \frac{U_0}{s}$

Utilizando la condición $\displaystyle U(l,s)=\frac{U_1}{s}$ y despejando $C_1$

$\displaystyle U(l,s) = C_1 \cosh{\sqrt{\frac{s}{k}} l} + \frac{U_0}{s}$

$\displaystyle \frac{U_1}{s} = C_1 \cosh{\sqrt{\frac{s}{k}} l} + \frac{U_0}{s}$

$\displaystyle \frac{U_1}{s} - \frac{U_0}{s} = C_1 \cosh{\sqrt{\frac{s}{k}} l}$

$\displaystyle \frac{U_1-U_0}{s\cosh{\sqrt{\frac{s}{k}} l}} = C_1$

$\displaystyle C_1 = \frac{U_1-U_0}{s\cosh{\sqrt{\frac{s}{k}} l}}$

Sustituyendo

$\displaystyle U(x,s) = C_1 \cosh{\sqrt{\frac{s}{k}} x} + \frac{U_0}{s}$

$\displaystyle U(x,s) = \left(\frac{U_1-U_0}{s\cosh{\sqrt{\frac{s}{k}} l}} \right) \cosh{\sqrt{\frac{s}{k}} x} + \frac{U_0}{s}$

Aplicando la $\displaystyle \mathcal{L}^{-1}$

$\displaystyle \mathcal{L}^{-1} [U(x,s)] = \mathcal{L}^{-1} \left[\left(\frac{U_1-U_0}{s\cosh{\sqrt{\frac{s}{k}} l}} \right) \cosh{\sqrt{\frac{s}{k}} x} \right] + \mathcal{L}^{-1} \left[\frac{U_0}{s} \right]$

$\displaystyle u(x,t) = (U_1 - U_0) \ \mathcal{L}^{-1} \left[\frac{\cosh{\sqrt{\frac{s}{k}} x}}{s\cosh{\sqrt{\frac{s}{k}} l}} \right] + U_0$

La transformada inversa de Laplace del primer término del segundo miembro se resolverá utilizando la fórmula de inversión compleja y el teorema de los residuos.

$\displaystyle \mathcal{L}^{-1} \left[\frac{\cosh{\sqrt{\frac{s}{k}} x}}{s\cosh{\sqrt{\frac{s}{k}} l}} \right] = \frac{1}{2\pi i} \int_{\gamma - i \infty}^{\gamma + i \infty}{\frac{e^{st} \cosh{\sqrt{\frac{s}{k}} x}}{s\cosh{\sqrt{\frac{s}{k}} l}} \ ds}$

$\displaystyle \mathcal{L}^{-1} \left[\frac{\cosh{\sqrt{\frac{s}{k}} x}}{s\cosh{\sqrt{\frac{s}{k}} l}} \right] = \frac{1}{2\pi i} \oint_C{\frac{e^{st} \cosh{\sqrt{\frac{s}{k}} x}}{s\cosh{\sqrt{\frac{s}{k}} l}} \ ds}$

Dentro de la integral de línea, la función $\displaystyle F(s)$ ,

$\displaystyle F(s) = \frac{e^{st} \cosh{\sqrt{\frac{s}{k}} x}}{s\cosh{\sqrt{\frac{s}{k}} l}}$

tiene polos simples en $s=0$ y $\displaystyle \sqrt{\frac{s}{k}} l = \left(n-\frac{1}{2} \right) \pi i$ para $n = 0,\pm 1, \pm 2, \cdots$ , es decir, $s=0$ y $\displaystyle s = - \frac{(2n-1)^2 \pi^2 k}{4l^2} = s_n$ para $n=1,2,3,\cdots$ .

Es así que,

$\displaystyle \mathcal{L}^{-1} \left[\frac{\cosh{\sqrt{\frac{s}{k}} x}}{s\cosh{\sqrt{\frac{s}{k}} l}} \right] =\sum{\text{residuos de } \frac{e^{st} \cosh{\sqrt{\frac{s}{k}} x}}{s\cosh{\sqrt{\frac{s}{k}} l}} \text{ en los polos } s=0 \text{ y } s=s_n}$

El residuo en $s=0$ es

$\displaystyle \lim_{s \rightarrow 0}{s \cdot \frac{e^{st} \cosh{\sqrt{\frac{s}{k}} x}}{s\cosh{\sqrt{\frac{s}{k}} l}}} = \lim_{s \rightarrow 0}{\frac{e^{st} \cosh{\sqrt{\frac{s}{k}} x}}{\cosh{\sqrt{\frac{s}{k}} l}}}$

$\displaystyle \lim_{s \rightarrow 0}{s \cdot \frac{e^{st} \cosh{\sqrt{\frac{s}{k}} x}}{s\cosh{\sqrt{\frac{s}{k}} l}}} = 1$

Y el residuo en $s=s_n$ es

$\displaystyle \lim_{s \rightarrow s_n}{(s-s_n) \cdot \frac{e^{st} \cosh{\sqrt{\frac{s}{k}} x}}{s\cosh{\sqrt{\frac{s}{k}} l}}} = \lim_{s \rightarrow s_n}{\frac{s-s_n}{\cosh{\sqrt{\frac{s}{k}} l}}} \cdot \lim_{s \rightarrow s_n}{\frac{e^{st} \cosh{\sqrt{\frac{s}{k}} x}}{s}}$

$\displaystyle \lim_{s \rightarrow s_n}{(s-s_n) \cdot \frac{e^{st} \cosh{\sqrt{\frac{s}{k}} x}}{s\cosh{\sqrt{\frac{s}{k}} l}}} = \lim_{s \rightarrow s_n}{\frac{1}{\frac{l}{2\sqrt{ks}} \cosh{\sqrt{\frac{s}{k}} l}}} \cdot \lim_{s \rightarrow s_n}{\frac{e^{st} \cosh{\sqrt{\frac{s}{k}} x}}{s}}$

$\displaystyle \lim_{s \rightarrow s_n}{(s-s_n) \cdot \frac{e^{st} \cosh{\sqrt{\frac{s}{k}} x}}{s\cosh{\sqrt{\frac{s}{k}} l}}} = \frac{1}{\frac{l}{2\sqrt{ks_n}} \cosh{\sqrt{\frac{s_n}{k}} l}} \frac{e^{s_n t} \cosh{\sqrt{\frac{s_n}{k}} x}}{s_n}$

$\displaystyle \lim_{s \rightarrow s_n}{(s-s_n) \cdot \frac{e^{st} \cosh{\sqrt{\frac{s}{k}} x}}{s\cosh{\sqrt{\frac{s}{k}} l}}} = \frac{4 {(-1)}^n}{(2n-1)\pi} e^{-(2n-1)^2 \pi^2 kt/4l^2} \cos{\frac{(2n-1) \pi x}{2l}}$

Regresando en la representación de la suma de residuos,

$\displaystyle \mathcal{L}^{-1} \left[\frac{\cosh{\sqrt{\frac{s}{k}} x}}{s\cosh{\sqrt{\frac{s}{k}} l}} \right] = 1 + \frac{4 {(-1)}^n}{(2n-1)\pi} e^{-(2n-1)^2 \pi^2 kt/4l^2} \cos{\frac{(2n-1) \pi x}{2l}}$

$\displaystyle \mathcal{L}^{-1} \left[\frac{\cosh{\sqrt{\frac{s}{k}} x}}{s\cosh{\sqrt{\frac{s}{k}} l}} \right] = 1 + \sum_{n=-\infty}^{\infty}{\frac{4 {(-1)}^n}{(2n-1)\pi} e^{-(2n-1)^2 \pi^2 kt/4l^2} \cos{\frac{(2n-1) \pi x}{2l}}}$

$\displaystyle \mathcal{L}^{-1} \left[\frac{\cosh{\sqrt{\frac{s}{k}} x}}{s\cosh{\sqrt{\frac{s}{k}} l}} \right] = \sum_{n=1}^{\infty}{\frac{4 {(-1)}^n}{(2n-1)\pi} e^{-(2n-1)^2 \pi^2 kt/4l^2} \cos{\frac{(2n-1) \pi x}{2l}}}$

$\displaystyle \mathcal{L}^{-1} \left[\frac{\cosh{\sqrt{\frac{s}{k}} x}}{s\cosh{\sqrt{\frac{s}{k}} l}} \right] = \frac{4}{\pi} \sum_{n=1}^{\infty}{\frac{{(-1)}^n}{(2n-1)} e^{-(2n-1)^2 \pi^2 kt/4l^2} \cos{\frac{(2n-1) \pi x}{2l}}}$

Y regresando a la solución de la ecuación diferencial y sustituyendo

$\displaystyle u(x,t) = (U_1 - U_0) \ \mathcal{L}^{-1} \left[\frac{\cosh{\sqrt{\frac{s}{k}} x}}{s\cosh{\sqrt{\frac{s}{k}} l}} \right] + U_0$

$\displaystyle u(x,t) = (U_1 - U_0) \ \frac{4}{\pi} \sum_{n=1}^{\infty}{\frac{{(-1)}^n}{(2n-1)} e^{-(2n-1)^2 \pi^2 kt/4l^2} \cos{\frac{(2n-1) \pi x}{2l}}} + U_0$

$\displaystyle u(x,t) = U_0 + \frac{4(U_1 - U_0)}{\pi} \sum_{n=1}^{\infty}{\frac{{(-1)}^n}{(2n-1)} e^{-(2n-1)^2 \pi^2 kt/4l^2} \cos{\frac{(2n-1) \pi x}{2l}}}$

Finalmente,

$\displaystyle \therefore u(x,t) = U_0 + \frac{4(U_1 - U_0)}{\pi} \sum_{n=1}^{\infty}{\frac{{(-1)}^n}{(2n-1)} e^{-(2n-1)^2 \pi^2 kt/4l^2} \cos{\frac{(2n-1) \pi x}{2l}}}$

Conducción del calor en una dimensión. Problemas de valor frontera. Laplace.

Introducción

Problemas resueltos

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta

Conducción del calor en una dimensión. Problemas de valor frontera. Laplace.

Introducción

Problemas resueltos

Comparte esto:

Relacionado

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta