Conducción del calor en un cilindro. Problemas de valor frontera. Laplace.

Introducción

La ecuación que se utiliza para determinar la conducción del calor en un cilindro es

$\displaystyle \frac{\partial u}{\partial t} = k \left(\frac{\partial^2 u}{\partial r^2} + \frac{1}{r} \frac{\partial u}{\partial r} \right)$

donde $u(x,t)$ es la temperatura en cualquier tiempo $t$ de un punto del sólido cilíndrico que está a una distancia $r$ del eje $x$ . Aquí se supondrá que el flujo de calor se representa solamente en dirección radial.

Problema resuelto

Problema. Un cilindro circular infinitamente largo y de radio unidad tiene una temperatura inicial constante $T$ . En $t=0$ se le aplica y se le mantiene una temperatura de 0°C en su superficie. Hallar la temperatura de cualquier punto del cilindro en cualquier punto posterior.

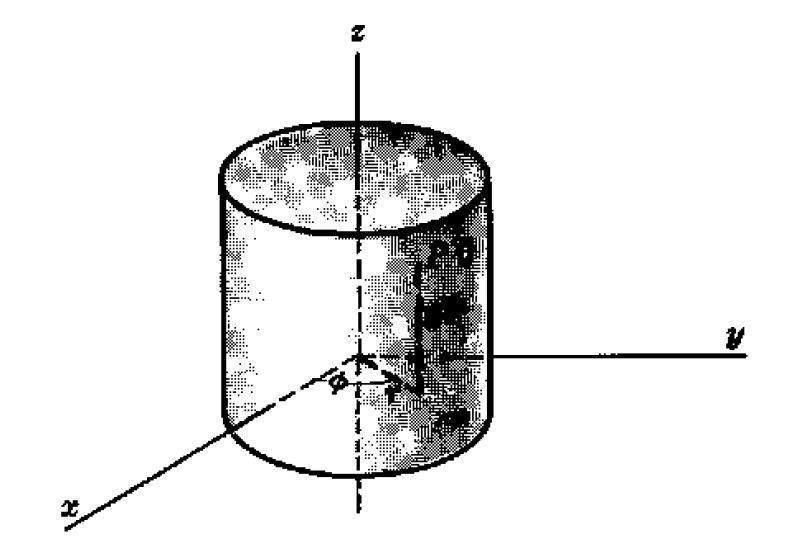
*Figura 1. Cilindro infinitamente largo.*

Solución. Si $(r, \phi, z)$ son las coordenadas cilíndricas de cualquier punto del cilindro y éste tiene como eje al eje $z$ (figura 1), es claro que la temperatura es independiente de $\phi$ y de $z$ ; por consiguiente se puede denotarla por $u(r,t)$ . El problema de valor frontera es

$\displaystyle \frac{\partial u}{\partial t} = k \left(\frac{\partial^2 u}{\partial r^2} + \frac{1}{r} \frac{\partial u}{\partial r} \right)$ donde $0<r<1$

Además,

$u(1,t) = 0$ , $u(r,0) = T$ , $|u(y,t)| < M$

Y sus transformadas de Laplace son

$\mathcal{L} [u(1,t)] = U(1,s) = 0$ y $\mathcal{L} [u(r,t) ] = U(r,s)$

Continuando, la ecuación anterior conviene reemplazar $t$ por $kt$ para tener esta nueva expresión

$\displaystyle \frac{\partial u}{\partial t} = \frac{\partial^2 u}{\partial r^2} + \frac{1}{r} \frac{\partial u}{\partial r}$

Su transformada de Laplace es

$\displaystyle \mathcal{L} \left[\frac{\partial u}{\partial t} \right] = \mathcal{L} \left[\frac{\partial^2 u}{\partial r^2} \right] + \frac{1}{r} \left[\frac{\partial u}{\partial r} \right]$

$\displaystyle s U(r,s) - u(r,0) = \frac{d^2 U}{dr^2} + \frac{1}{r} \frac{dU}{dr}$

$\displaystyle s U(r,s) - T = \frac{d^2 U}{dr^2} + \frac{1}{r} \frac{dU}{dr}$

$\displaystyle \frac{d^2 U}{dr^2} + \frac{1}{r} \frac{dU}{dr} - s U(r,s) = - T$

La solución general de esta ecuación diferencial es

$\displaystyle U(r,s) = C_1 J_0 (i \sqrt{s} r) + C_2 Y_0 (i \sqrt{s} r) + \frac{T}{s}$

Como $Y_0 (i \sqrt{s} r)$ está acotada cuando $r \rightarrow 0$ , se tiene que tomar $C_2 = 0$ . Entonces,

$\displaystyle U(r,s) = C_1 J_0 (i \sqrt{s} r) + \frac{T}{s}$

Cuando $U(1,s)=0$ , el valor de $C_1$ es

$\displaystyle U(1,s) = C_1 J_0 (i \sqrt{s}(1)) + \frac{T}{s}$

$\displaystyle 0 = C_1 J_0 (i \sqrt{s}) + \frac{T}{s}$

$\displaystyle C_1 = - \frac{T}{s J_0 (i \sqrt{s})}$

Así que

$\displaystyle U(r,s) = C_1 J_0 (i \sqrt{s} r) + \frac{T}{s}$

$\displaystyle U(r,s) = - \frac{T}{s J_0 (i \sqrt{s})} J_0 (i \sqrt{s} r) + \frac{T}{s}$

$\displaystyle U(r,s) = \frac{T}{s} - \frac{T J_0 (i \sqrt{s} r)}{s J_0 (i \sqrt{s})}$

Aplicando la transformada inversa de Laplace

$\displaystyle \mathcal{L} ^{-1} [U(r,s)] = T \ \mathcal{L} \left[\frac{1}{s} \right] - T \ \mathcal{L}^{-1} \left[\frac{J_0 (i \sqrt{s} r)}{s J_0 (i \sqrt{s})} \right]$

$\displaystyle u(r,t) = T - T \ \mathcal{L}^{-1} \left[\frac{J_0 (i \sqrt{s} r)}{s J_0 (i \sqrt{s})} \right]$

Resolviendo el segundo término del segundo miembro por la fórmula de inversión compleja

$\displaystyle \mathcal{L}^{-1} \left[\frac{J_0 (i \sqrt{s} r)}{s J_0 (i \sqrt{s})} \right] = \frac{1}{2\pi i} \int_{\gamma - i \infty}^{\gamma + i \infty}{e^{st} \cdot \left[\frac{J_0 (i \sqrt{s} r)}{s J_0 (i \sqrt{s})} \right] ds}$

$\displaystyle \mathcal{L}^{-1} \left[\frac{J_0 (i \sqrt{s} r)}{s J_0 (i \sqrt{s})} \right] = \frac{1}{2\pi i} \oint_{C}{\frac{e^{st} J_0 (i \sqrt{s} r)}{s J_0 (i \sqrt{s})} \ ds}$

Ahora $J_0 (i \sqrt{s})$ tiene ceros simples cuando $i \sqrt{s} = \lambda_1, \lambda_2, \cdots, \lambda_n$ . Así, el integrando tiene polos simples en $s=- \lambda_n^2$ , $n=1,2,3,\cdots$ y también en $s=0$ . Así que

$\displaystyle \mathcal{L}^{-1} \left[\frac{J_0 (i \sqrt{s} r)}{s J_0 (i \sqrt{s})} \right] = \sum{\text{ residuos de } \frac{e^{st} J_0 (i \sqrt{s} r)}{s J_0 (i \sqrt{s})} \ \text{ en los polos } s=0 \text{ y } s=-\lambda_n^2}$

El residuo en $s=0$ es

$\displaystyle \lim_{s \rightarrow 0}{s \cdot \frac{e^{st} J_0 (i \sqrt{s} r)}{s \ J_0 (i \sqrt{s})}} = \lim_{s \rightarrow 0}{\frac{e^{st} J_0 (i \sqrt{s} r)}{J_0 (i \sqrt{s})}}$

$\displaystyle \lim_{s \rightarrow 0}{s \cdot \frac{e^{st} J_0 (i \sqrt{s} r)}{s \ J_0 (i \sqrt{s})}} = 1$

El residuo en $s=-\lambda_n^2$ es

$\displaystyle \lim_{s \rightarrow - \lambda_n^2}{(s+\lambda_n^2) \cdot \frac{e^{st} J_0 (i \sqrt{s} r)}{s \ J_0 (i \sqrt{s})}} = \lim_{s \rightarrow - \lambda_n^2}{\frac{s+\lambda_n^2}{J_0 (i \sqrt{s})}} \cdot \lim_{s \rightarrow -\lambda_n^2}{\frac{e^{st} J_0 (i \sqrt{s} r)}{s}}$

$\displaystyle \lim_{s \rightarrow - \lambda_n^2}{(s+\lambda_n^2) \cdot \frac{e^{st} J_0 (i \sqrt{s} r)}{s \ J_0 (i \sqrt{s})}} = \lim_{s \rightarrow - \lambda_n^2}{\frac{1}{\frac{1}{2\sqrt{s}} J'_0 (i \sqrt{s})}} \cdot \lim_{s \rightarrow -\lambda_n^2}{\frac{e^{st} J_0 (i \sqrt{s} r)}{s}}$

$\displaystyle \lim_{s \rightarrow - \lambda_n^2}{(s+\lambda_n^2) \cdot \frac{e^{st} J_0 (i \sqrt{s} r)}{s \ J_0 (i \sqrt{s})}} = \lim_{s \rightarrow - \lambda_n^2}{\frac{2 \sqrt{s}}{J'_0 (i \sqrt{s})}} \cdot \lim_{s \rightarrow -\lambda_n^2}{\frac{e^{st} J_0 (i \sqrt{s} r)}{s}}$

$\displaystyle \lim_{s \rightarrow - \lambda_n^2}{(s+\lambda_n^2) \cdot \frac{e^{st} J_0 (i \sqrt{s} r)}{s \ J_0 (i \sqrt{s})}} = \frac{2 \sqrt{-\lambda_n^2}}{J'_0 (i \sqrt{- \lambda_n^2})} \cdot \frac{e^{- \lambda_n^2 t} J_0 (i \sqrt{-\lambda_n^2} r)}{\lambda_n^2}$

$\displaystyle \lim_{s \rightarrow - \lambda_n^2}{(s+\lambda_n^2) \cdot \frac{e^{st} J_0 (i \sqrt{s} r)}{s \ J_0 (i \sqrt{s})}} = \frac{2 e^{-\lambda_n^2 t} J_0 (\lambda_n r)}{\lambda_n J_0 (\lambda_n)}$

$\displaystyle \lim_{s \rightarrow - \lambda_n^2}{(s+\lambda_n^2) \cdot \frac{e^{st} J_0 (i \sqrt{s} r)}{s \ J_0 (i \sqrt{s})}} = - \frac{2 e^{-\lambda_n^2 t} J_0 (\lambda_n r)}{\lambda_n J_1 (\lambda_n)}$

Regresando,

$\displaystyle \mathcal{L}^{-1} \left[\frac{J_0 (i \sqrt{s} r)}{s J_0 (i \sqrt{s})} \right] = 1 - \sum_{n=1}^{\infty}{\frac{2 e^{-\lambda_n^2 t} J_0 (\lambda_n r)}{\lambda_n J_1 (\lambda_n)}}$

Regresando una vez más,

$\displaystyle u(r,t) = T - T \ \mathcal{L}^{-1} \left[\frac{J_0 (i \sqrt{s} r)}{s J_0 (i \sqrt{s})} \right]$

$\displaystyle u(r,t) = T - T \left[1 - \sum_{n=1}^{\infty}{\frac{2 e^{-\lambda_n^2 t} J_0 (\lambda_n r)}{\lambda_n J_1 (\lambda_n)}} \right]$

$\displaystyle u(r,t) = T - T + T \sum_{n=1}^{\infty}{\frac{2 e^{-\lambda_n^2 t} J_0 (\lambda_n r)}{\lambda_n J_1 (\lambda_n)}}$

$\displaystyle u(r,t) = T \sum_{n=1}^{\infty}{\frac{2 e^{-\lambda_n^2 t} J_0 (\lambda_n r)}{\lambda_n J_1 (\lambda_n)}}$

$\displaystyle u(r,t) = 2T \sum_{n=1}^{\infty}{\frac{2 e^{-\lambda_n^2 t} J_0 (\lambda_n r)}{\lambda_n J_1 (\lambda_n)}}$

Reemplazando $t$ por $kt$

$\displaystyle u(r,t) = 2T \sum_{n=1}^{\infty}{\frac{2 e^{-k \lambda_n^2 t} J_0 (\lambda_n r)}{\lambda_n J_1 (\lambda_n)}}$

Finalmente,

$\displaystyle \therefore u(r,t) = 2T \sum_{n=1}^{\infty}{\frac{2 e^{-k \lambda_n^2 t} J_0 (\lambda_n r)}{\lambda_n J_1 (\lambda_n)}}$

Conducción del calor en un cilindro. Problemas de valor frontera. Laplace.

Introducción

Problema resuelto

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta

Conducción del calor en un cilindro. Problemas de valor frontera. Laplace.

Introducción

Problema resuelto

Comparte esto:

Relacionado

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta