Vectores unitarios y el círculo unitario. Cálculo vectorial.

Vectores unitarios canónicos o estándar

Los vectores unitarios (1, 0) y (0, 1) se les llama vectores unitarios canónicos o estándar en el plano y se denotan por

Para el vector canónico en el eje $x$ : $\bold{i} = (1, 0)$
Para el vector canónico en el eje $y$ : $\bold{j} = (0, 1)$

Figura 1. Representación gráfica de los vectores unitarios canónicos.

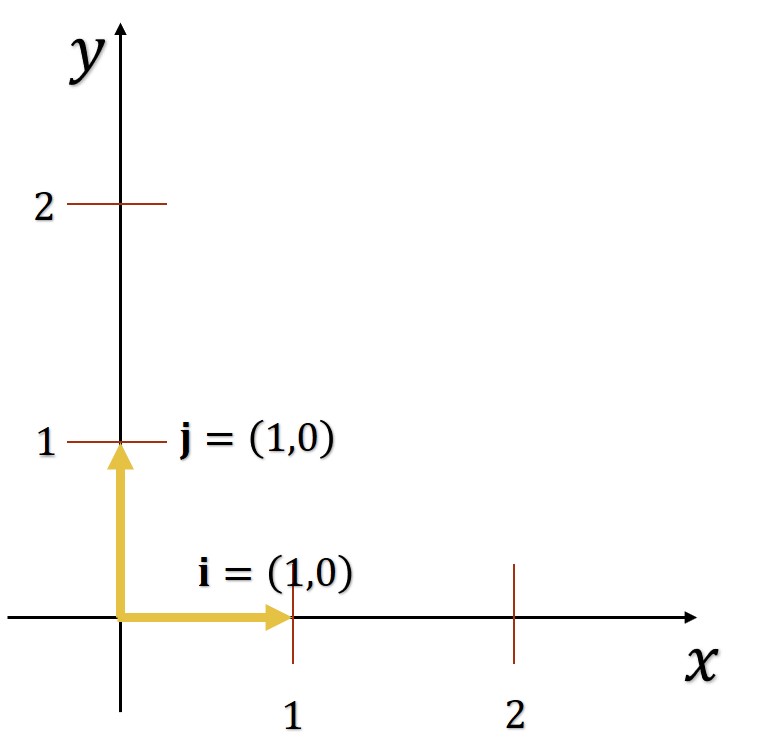
Estos vectores pueden usarse para representar cualquier vector de manera única, es decir

$\bold{v} = (v_1 , v_2) = (v_1, 0) + (0 , v_2)$

$\bold{v} = (v_1 , v_2) = v_1(1, 0) + v_2(0 , 1)$

$\bold{v} = (v_1 , v_2) = v_1 \bold{i} + v_2 \bold{j}$

Al vector $\bold{v} = {v}_{1} \bold{i} + {v}_{2} \bold{j}$ se le llama una combinación lineal de i y j. A los escalares $v_1$ y $v_2$ se les llama componentes horizontal y vertical de v.

Problema resuelto

Problema. Sea u el vector con punto inicial (2,-5) y punto final (-1,3), y sea v = 2i – j. Expresar cada vector como combinación lineal de i y j, donde

a) u
b) w = 2u – 3v

Solución a). Primer se obtiene el vector basándose en el punto inicial $[P({p}_{1}, {p}_{2})]$ y el punto final $[Q({q}_{1}, {q}_{2})]$

$\bold{u} = ({q}_{1} - {p}_{1}, {q}_{2} - {p}_{2})$

$\bold{u} = [-1-2,3-(-5)]$

$\therefore \bold{u} = (-3,8) = -3\bold{i} + 8\bold{j}$

Solución b). Realizando la operación indicada

$\bold{w} = 2\bold{u} - 3\bold{v}$

$\bold{w} = 2(-3\bold{i} + 8\bold{j}) - 3(2\bold{i} - \bold{j})$

$\bold{w} = - 6\bold{i} + 16\bold{j} - 6\bold{i} + 3\bold{j}$

$\therefore \bold{w}= -12\bold{i} + 19\bold{j}$

Circulo unitario

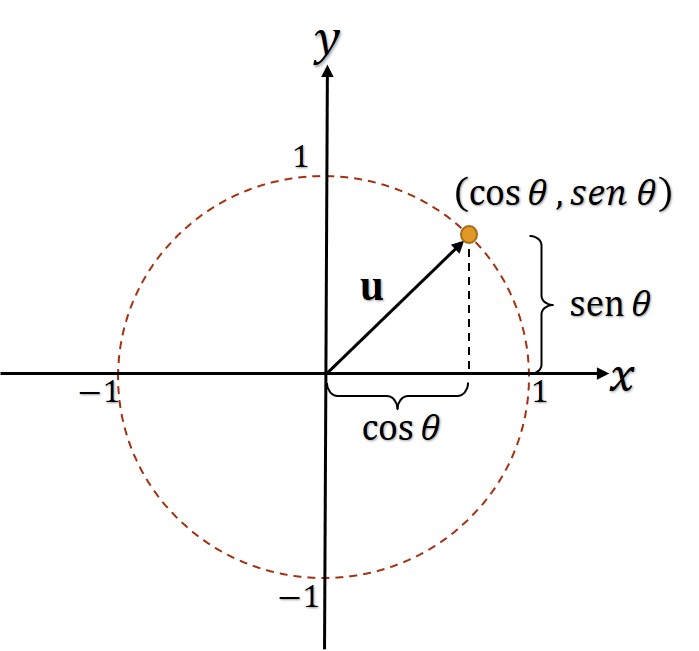
Si u es un vector unitario y 𝜃 es el ángulo (medido en sentido contrario a las manecillas del reloj) desde el eje x positivo hasta u, el punto final de u está en el círculo unitario, y se tiene

$\bold{u} = (\cos{\theta} ,\sin{\theta}) = (\cos{\theta})\bold{i} + (\sin{\theta})\bold{j}$

Además, cualquier vector distinto de cero v que forma un ángulo 𝜃 con el eje $x$ positivo tiene la misma dirección que u y se puede expresar como

$\bold{u} = ||\bold{v}||(\cos{\theta},\sin{\theta}) = ||\bold{v}||\cos{\theta}\bold{i} + ||\bold{v}||\sin{\theta} \bold{j}$

Figura 1. Representación gráfica del círculo unitario.

Problema resuelto

Problema. El vector v tiene una magnitud de 3 y forma un ángulo de 30° con el eje $x$ positivo. Expresar v como combinación lineal de los vectores unitarios i y j.

Solución. Usando la fórmula

$\bold{u} = ||\bold{v}||(\cos{\theta},\sin{\theta}) = ||\bold{v}||(\cos{\theta} \bold{i} + \sin{\theta} \bold{j})$

$\bold{u} = ||\bold{v}||\cos{\theta} \bold{i} + ||\bold{v}||\sin{\theta} \bold{j}$

Y sustituyendo

$\displaystyle \bold{v} = 3(\cos{30}, \sin{30}) = 3\left(\frac{\sqrt{3}}{2} \bold{i} + \frac{1}{2} \bold{j}\right) = \frac{3\sqrt{3}}{2} \bold{i} + \frac{3}{2} \bold{j}$

$\displaystyle \therefore \bold{v} = \frac{3\sqrt{3}}{2} \bold{i} + \frac{3}{2} \bold{j}$

Vectores unitarios y el círculo unitario. Cálculo vectorial.

Vectores unitarios canónicos o estándar

Problema resuelto

Circulo unitario

Problema resuelto

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta

Vectores unitarios y el círculo unitario. Cálculo vectorial.

Vectores unitarios canónicos o estándar

Problema resuelto

Circulo unitario

Problema resuelto

Comparte esto:

Relacionado

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta