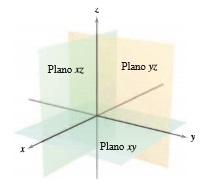
Se parte con identificar puntos en el sistema de coordenadas tridimensional. Se puede construir este sistema trazando en el origen un eje z perpendicular al eje x y al eje y. La figura 1 muestra la porción positiva de cada eje de coordenadas.

Tomados por pares, los ejes determinan tres planos coordenados: el plano xy, el plano xz y el plano yz. Estos tres planos coordenados dividen el espacio tridimensional en ocho octantes.

Figura 1. Sistema de coordenadas tridimensional. Nodo Universitario de la Universidad de Guanajuato, Introducción a la geometría analítica del espacio. [Figura]. Recuperado de: https://oa.ugto.mx

En este sistema tridimensional, un punto P en el espacio está determinado por una terna ordenada (x,y,z) donde x, y y z son:

  • x es la distancia dirigida que va del plano yz a P
  • y es la distancia dirigida que va del plano xz a P
  • z es la distancia dirigida que va del plano xy a P

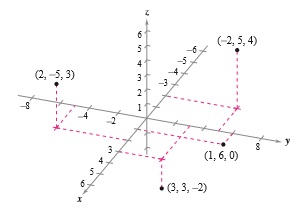
En la figura 2 se muestran varios puntos representados en un sistema de coordenadas tridimensional.

Figura 2. Puntos que se muestran en el sistema de coordenadas tridimensional. Nodo Universitario de la Universidad de Guanajuato, Introducción a la geometría analítica del espacio. [Figura]. Recuperado de: https://oa.ugto.mx

Un sistema de coordenadas tridimensional puede tener una orientación levógira o dextrógira. Para determinar la orientación de un sistema, se puede imaginar de pie en el origen, con los brazos apuntando en dirección de los ejes x y y positivo y el eje z apuntando hacia arriba. El sistema es dextrógiro o levógiro dependiendo de qué mano queda apuntando a lo largo del eje x.

Avatar de Desconocido

Publicado por Cesar Reyes

Dedicado a compartir información temas referentes al cálculo básicos, intermedios y avanzados mediante presentaciones PDF, videos y publicaciones en este sitio web.

Deja un comentario

Este sitio utiliza Akismet para reducir el spam. Conoce cómo se procesan los datos de tus comentarios.