Ángulo entre dos vectores. Cálculo vectorial.

Introducción

El ángulo entre dos vectores distintos de cero es el ángulo $\theta$ , $0 \le \theta \le \pi$ , entre sus respectivos vectores en posición canónica o estándar, como se muestra en la figura 1.

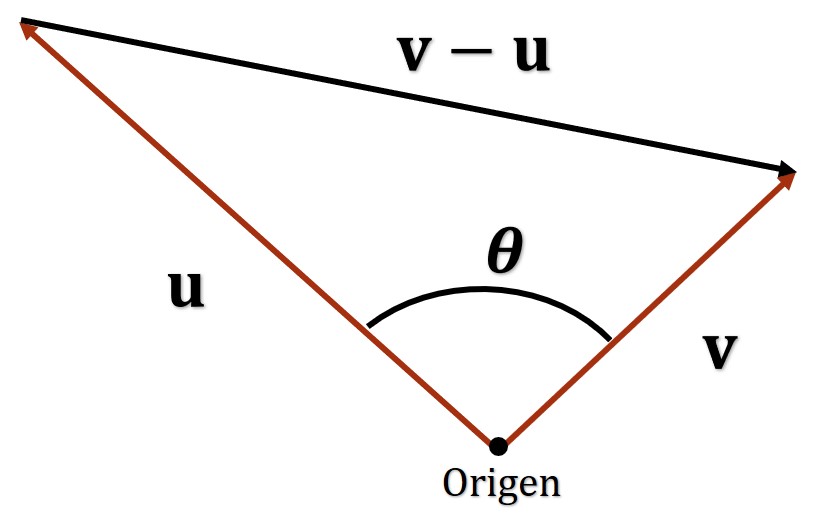
Figura 1. Representación gráfica del ángulo entre dos vectores.

Si 𝜃 es el ángulo entre dos vectores distintos de cero u y v, entonces:

$\displaystyle \cos{\theta} = \frac{(\bold{u} \cdot \bold{v})}{||\bold{u}|| \cdot ||\bold{v}||}$

Si el ángulo entre dos vectores es conocido, lo anterior se puede reescribir en la forma

$\displaystyle \bold{u} \cdot \bold{v} = ||\bold{u}|| ||\bold{v}|| \cos{\theta}$

se obtiene una alternativa de calcular el producto escalar. De esta forma, se puede puede ver que como ||u|| y ||v|| son siempre positivos, $\bold{u} \cdot \bold{v}$ y $\cos{\theta}$ siempre tendrá el mismo signo. En la figura 2 se muestra las orientaciones posibles de los dos vectores.

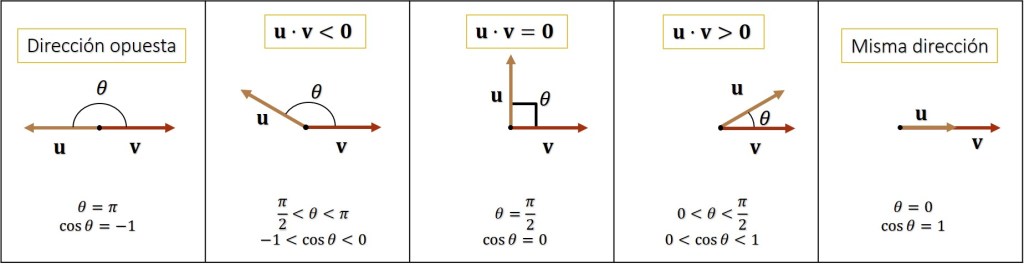
Figura 2. Orientaciones posibles de dos vectores.

Se puede ver que dos vectores distintos de cero forman un ángulo recto si y sólo si su producto escalar es cero; entonces se dice que los dos vectores son ortogonales.

Los vectores son ortogonales si $\bold{u} \cdot \bold{v} = 0$ .

Los términos «perpendicular», «ortogonal» y «normal» significan esencialmente lo mismo: formar un ángulos rectos. Sin embargo, es común que dos vectores son ortogonales, dos rectas o planos son perpendiculares y que un vector es normal a una recta o plano dado.

Problema resuelto

Problema. Si u = (3,-1,2), v = (-4,0,2), w = (1,-1,-2) y z = (2,0,-1), hallar el ángulo entre cada uno de los siguientes pares de vectores:

a) $\bold{u}$ y $\bold{v}$
b) $\bold{u}$ y $\bold{w}$
c) $\bold{v}$ y $\bold{z}$

Solución a).

$\displaystyle \cos{\theta} = \frac{(\bold{u} \cdot \bold{v})}{||\bold{u}|| \cdot ||\bold{v}||} = \frac{(3, -1, 2) \cdot (-4, 0, 2)}{\sqrt{14} \cdot \sqrt{20}}$

$\displaystyle \cos{\theta} = \frac{-12+0+4}{\sqrt{280}} = \frac{-8}{\sqrt{280}} = \frac{-4}{\sqrt{70}}$

$\displaystyle \theta = \arccos{\left(\frac{-4}{\sqrt{70}} \right)}$

$\theta = 118.5608$ °

Solución b)

$\displaystyle \cos{\theta} = \frac{(\bold{u} \cdot \bold{w})}{||\bold{u}|| \cdot ||\bold{w}||} = \frac{(3, -1, 2) \cdot (1, -1, -2)}{\sqrt{14} \cdot \sqrt{6}}$

$\displaystyle = \frac{(3 + 1 - 4)}{\sqrt{84}} = \frac{0}{\sqrt{84}} = 0$

$\theta = \arccos{0}$

$\therefore \theta = 90$ °

Se dice que los vectores u y w son paralelos.

Solución c)

$\displaystyle \cos{\theta} = \frac{(\bold{v} \cdot \bold{z})}{||\bold{v}|| \cdot ||\bold{z}||} = \frac{(-4, 0, 2) \cdot (2, 0, -1)}{\sqrt{20} \sqrt{5}}$