Distancia de dos puntos en el espacio. Cálculo vectorial.

Introducción

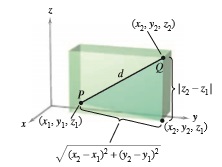
Para encontrar la distancia entre dos puntos en el espacio, se utiliza dos veces el teorema de Pitágoras. Posteriormente, se obtiene la fórmula de la distancia entre los puntos $(x_1, y_1, z_1)$ y $(x_2, y_2, z_2)$ .

$\displaystyle d = \sqrt{{(x_2-x_1)}^2 + {(y_2-y_1)}^2 + {(z_2-z_1)}^2}$

Figura 1. Distancia entre dos puntos en el espacio. Nodo Universitario de la Universidad de Guanajuato, Introducción a la geometría analítica del espacio. [Figura]. Recuperado de: https://oa.ugto.mx

Problemas resueltos

Problema 1. Hallar la distancia entre los puntos $(2,-1,3)$ y $(1,0,-2)$ .

Solución. Se identifica que

$(2,-1,3) = (x_1, y_1, z_1)$ y $(1,0,-2) = (x_2, y_2, z_2)$

Tomando la fórmula y sustituyendo

$\displaystyle d = \sqrt{{(x_2-x_1)}^2 + {(y_2-y_1)}^2 + {(z_2-z_1)}^2}$

$\displaystyle d = \sqrt{{(1-2)}^2 + {[0-(-1)]}^2 + {(-2-3)}^2}$

$\displaystyle d = \sqrt{{(-1)}^2 + {(1)}^2 + {(-5)}^2}$

$\displaystyle d = \sqrt{1 + 1 + 25}$

$\displaystyle \therefore d = \sqrt{27} = 3 \sqrt{3}$

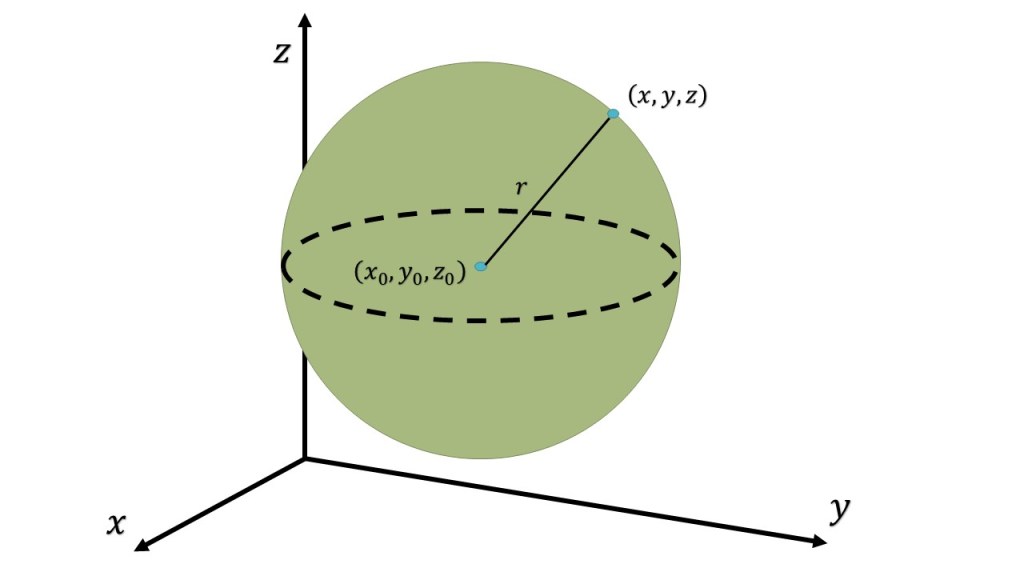
El radio de una esfera

Una esfera con centro en $(x_0, y_0, z_0)$ y radio $r$ está definida como el conjunto de todos los punto $(x,y,z)$ tales que la distancia entres $(x,y,z)$ y $(x_0, y_0, z_0)$ es $r$ . Se puede usar la fórmula de la distancia para encontrar la ecuación canónica o estándar de una esfera de radio $r$ , con centro en $(x_0, y_0, z_0)$ . Si $(x, y, z)$ es un punto arbitrario en la esfera, la ecuación de la esfera es

${(x-x_0)}^2 + {(y-y_0)}^2 + {(z-z_0)}^2 = r^2$

El punto punto medio del segmento de recta que une a los puntos $(x_1, y_1, z_1)$ y $(x_2, y_2, z_2)$ tiene coordenadas

$\displaystyle \left(\frac{x_1+x_2}{2}, \frac{y_1+y_2}{2}, \frac{z_1+z_2}{2} \right)$

Problema resuelto

Problema. Hallar la ecuación canónica o estándar de la esfera que tiene los puntos $(5,-2,3)$ y $(0,4, -3)$ como extremos de un diámetro.

Solución. Por regla del punto medio, el centro de la esfera es

$\displaystyle \left(\frac{x_1+x_2}{2}, \frac{y_1+y_2}{2}, \frac{z_1+z_2}{2} \right)$

$\displaystyle \left(\frac{5+0}{2}, \frac{-2+4}{2}, \frac{3-3}{2} \right)$

$\displaystyle \left(\frac{5}{2}, \frac{2}{2}, \frac{0}{2} \right)$

$\displaystyle \left(\frac{5}{2}, 1, 0 \right)$

Después, el radio se calcula utilizando la fórmula de la distancia; puede obtenerse de dos maneras

Por último, la ecuación canónica de la esfera es

${(x-x_0)}^2 + {(y-y_0)}^2 + {(z-z_0)}^2 = r^2$

$\displaystyle {\left(x- \frac{5}{2} \right)}^2 + {(y-1)}^2 + {(z-0)}^2 = \left(\frac{\sqrt{97}}{2}\right)^2$

$\displaystyle {\left(x- \frac{5}{2} \right)}^2 + {(y-1)}^2 + {z}^2 = \frac{97}{4}$

Tomando los puntos $\displaystyle \left(\frac{5}{2}, 1, 0 \right)$ y $(0,4,-3)$	Tomando los puntos $\displaystyle \left(\frac{5}{2}, 1, 0 \right)$ y $(5,-2,3)$
$\displaystyle d = \sqrt{{\left(0 - \frac{5}{2} \right)}^2 + {(4-1)}^2 + {(-3-0)}^2}$ $\displaystyle d = \sqrt{{\left(- \frac{5}{2} \right)}^2 + {(3)}^2 + {(-3)}^2}$ $\displaystyle d = \sqrt{\frac{25}{4} + 9 + 9}$ $\displaystyle d = \sqrt{\frac{97}{4}}$ $\displaystyle d = \frac{\sqrt{97}}{2}$	$\displaystyle d = \sqrt{{\left(5 - \frac{5}{2} \right)}^2 + {(-2-1)}^2 + {(3-0)}^2}$ $\displaystyle d = \sqrt{{\left(\frac{5}{2} \right)}^2 + {(-3)}^2 + {(3)}^2}$ $\displaystyle d = \sqrt{\frac{25}{4} + 9 + 9}$ $\displaystyle d = \frac{\sqrt{97}}{2}$

Distancia de dos puntos en el espacio. Cálculo vectorial.

Introducción

Problemas resueltos

El radio de una esfera

Problema resuelto

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta

Distancia de dos puntos en el espacio. Cálculo vectorial.

Introducción

Problemas resueltos

El radio de una esfera

Problema resuelto

Comparte esto:

Relacionado

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta